2.1探索勾股定理教学设计
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2.1探索勾股定理
一.教学目标
(一)知识点
1.体验勾股定理的探索过程,由特例猜想勾股定理,再由特例验证勾股定理.
2.会利用勾股定理解释生活中的简单现象.
(二)能力训练要求
1.在学生充分观察、归纳、猜想、探索勾股定理的过程中,发展合情推理能力,体会数形结合的思想.
2.在探索勾股定理的过程中,发展学生归纳、概括和有条理地表达活动过程及结论的能力.
(三)情感与价值观要求
1.培养学生积极参与、合作交流的意识.
2.在探索勾股定理的过程中,体验获得成功的快乐,锻炼学生克服困难的勇气.
二.教学重、难点
重点:探索和验证勾股定理.
难点:在方格纸上通过计算面积的方法探索勾股定理.
三.教学方法
交流—探索—猜想.
在方格纸上,同学们通过计算以直角三角形的三边为边长的三个正方形的面积,在合作交流的过程中,比较这三个正方形的面积,由此猜想出直角三角形的三边关系.
四.教具准备
1.学生每人课前准备若干张方格纸.
2.投影片三张:
第一张:填空(记作§2.1 A);
第二张:问题串(记作§2.1 B);
第三张:做一做(记作§2.1 C).
五.教学过程
Ⅰ.创设问题情境,引入新课
出示投影片(§2.1 A)
(1)三角形按角分类,可分为_________、_________、_________.(2)对于一般的三角形来说,判断它们全等的条件有哪些?对于直角三角形呢?(3)有两个直角三角形,如果有两条边对应相等,那么这两个直角三角形一定全等吗?
[师]上面三个小问题是我们以前讨论过的,我们简单的回忆一下.
[生](1)三角形按角的大小来分类可分为:直角三角形、锐角三角形、钝角三角形;
(2)对于一般三角形来说,我们可以用SAS(边角边)、ASA(角边角)、AAS(角角边)、SSS(边边边)来判断两个三角形全等;而对于直角三角形来说,除以上四种方法外,还可以用HL(即有斜边和一条直角边对应相等的两个直角三角形全等).
(3)两个直角三角形,有两边对应相等,有两种情况:
第一种情况:两条直角边对应相等,这时,我们可注意到它们的夹角也对应相等,利用SAS可判断它们全等.
第二种情况:一条直角边和斜边对应相等,利用HL公理即可判断它们全等.
综上所述,两个直角三角形,如果有两边对应相等,则这两个直角三角形全等.
[师]我们可以注意到直角三角形有它独有的一些特征.在我们学习和生活中,你是否还发现直角三角形的其他特征呢?
这节课,我们就来继续研究直角三角形.
Ⅱ.讲述新课
1.问题串
[师](出示投影片§2.1 B)[来源:21世纪教育网]
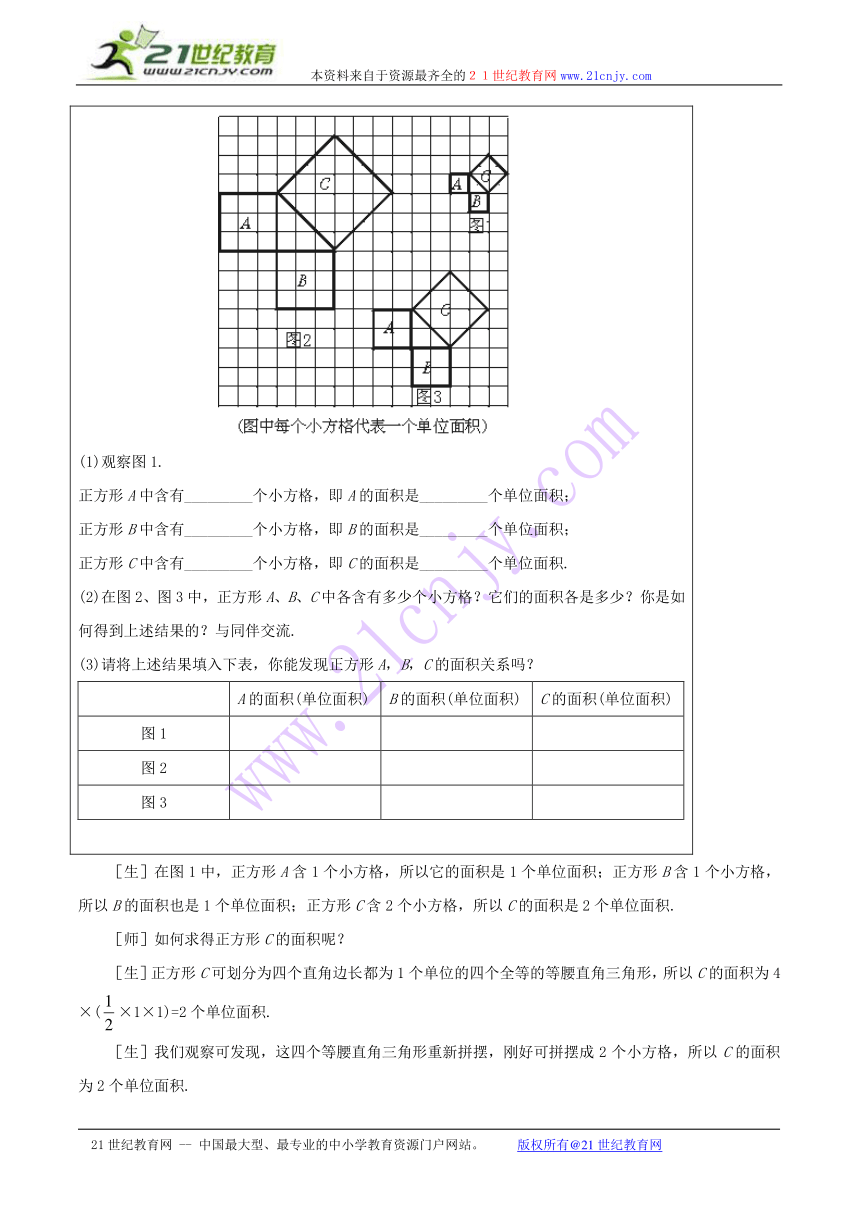
观察下图,并回答问题:[来源:21世纪教育网](1)观察图1.正方形A中含有_________个小方格,即A的面积是_________个单位面积;正方形B中含有_________个小方格,即B的面积是_________个单位面积;正方形C中含有_________个小方格,即C的面积是_________个单位面积.21世纪教育网(2)在图2、图3中,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流.(3)请将上述结果填入下表,你能发现正方形A,B,C的面积关系吗?21世纪教育网A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图1图2图321世纪教育网
[生]在图1中,正方形A含1个小方格,所以它的面积是1个单位面积;正方形B含1个小方格,所以B的面积也是1个单位面积;正方形C含2个小方格,所以C的面积是2个单位面积.
[师]如何求得正方形C的面积呢?
[生]正方形C可划分为四个直角边长都为1个单位的四个全等的等腰直角三角形,所以C的面积为4×(×1×1)=2个单位面积.
[生]我们观察可发现,这四个等腰直角三角形重新拼摆,刚好可拼摆成2个小方格,所以C的面积为2个单位面积.
[生]正方形C还可以看成边长为2个单位的正方形面积的一半,即C的面积为×22=2个单位面积.
[师]同学们能够不拘一格地积极思考问题,用多种方法去求得图1中C的面积,值得发扬广大,那么图2,图3中的A,B,C的面积是否可借鉴图1中的A,B,C的求法获得呢?请与你的同学们讨论、交流。
[生]图2中,A含有9个小方格或者说正方形A的边长是3个单位长度,都可以求得A的面积是9个单位面积;同理可求得B含有9个小方格,所以B的面积为9个单位面积;对于正方形C来说,我们观察可发现它含有18个小方格,所以C的面积为18个单位面积.
[师]看来,同学们已能从图2中很容易地就求得了A,B,C的面积.是不是在求C的面积时也和图1相类似,有多种求法呢?
[生]是的.在正方形C中,我们可以把它的边缘的12个全等的等腰直角三角形拼摆成6个小方格,再加上中间的12个小方格,正方形C共含有18个小方格,所以它的面积为18个单位面积;我们也可以把C分割成四个直角边为3个单位长度的等腰直角三角形,也可算得C的面积为4×(×32)=18个单位面积.
[生]如果把组成C的四个等腰直角三角形沿正方形的边向外翻,我们观察又可发现C在边长为6个单位长度的正方形中,并且C的面积恰好是这个正方形面积的一半即×62=18个单位面积.
[生]图3与图1,图2类似,所以我们可用同样的方法观察求得A,B,C各含4个,4个,8个小方格,面积分别为4个,4个,8个单位面积.
[师]把三个图中A,B,C的面积分别填入上面的表格中,你能发现它们的关系吗?
[生]C的面积=A的面积+B的面积.
(表格略)21世纪教育网
[师]很好!但是A,B,C的面积为什么会有这种关系呢?我们接着观察这三个图,你能发现什么?
[生]在前面您说过这节课我们主要研究直角三角形,而在这三个图中,都是三个正方形围着一个直角三角形.
[师]的确如此,从图中我们可以发现:三个正方形好像是“长”在直角三角形的三边上.
[生]这说明三个正方形的边长分别是以直角三角形的三边为边长得到的.
[师]那么,(3)的结论即C的面积=A的面积+B的面积与三角形有什么关系?这个关系说明什么?大家可以讨论、交流.
[生]C是斜边上的正方形,所以C的面积是斜边的平方;A,B是两直角边上的正方形,所以A,B的面积分别是这两条直角边的平方.根据A,B,C的面积关系,我们不难发现:斜边的平方就等于两直角边的平方和.
[师]但是,我们也不难发现上面3个图中的直角三角形是等腰直角三角形?如果不是等腰直角三角形,而是一般的直角三角形,会不会也有这种三边关系呢?
2.做一做
出示投影片(§2.1 C)
(1)观察图4,图5,并填写下表:A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图4[来源:21世纪教育网]图5你是怎样得到上面结果的?与同伴交流.(2)三个正方形A,B,C的面积之间的关系?
(让学生先独立思考,然后填写上面的表格.最后以小组为单位充分交流各自的想法,特别是在计算斜边上的正方形的面积即正方形C的求法)
[师生共析]根据图4,图5可填表如下:
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图4 16 9 25
图5 4 9 1321世纪教育网
我们先来观察图4,不难看出A,B分别含有16个小方格,9个小方格,所以A、B的面积分别为16个单位面积,9个单位面积,但斜边上的正方形C的面积的计算较为复杂,我们可用以下几种方法求得:
第一种方法:将正方形C分割成4个直角边长分别为3、4全等的直角三角形和中间的一个小方格,利用计算三角形面积的公式可得正方形C的面积为4×(×3×4)+1=24+1=25个单位面积.
第二种方法:直接数正方形C中含有多少个小方格,但需要适当的拼凑,在第一种方法中,我们将正方形分割成5部分,直角三角形Ⅰ、Ⅱ、Ⅲ、Ⅳ和一个小方格,其中直角三角形Ⅰ、Ⅲ可拼凑成一个长和宽分别为3和4的长方形,含有12个小方格,同理Ⅱ、Ⅳ也可拼凑成12个小方格,所以正方形C中共有12+12+1=25个小方格即C的面积为25个单位面积.
第三种方法:可将直角三角形Ⅰ、Ⅱ、Ⅲ、Ⅳ沿正方形C的边外翻,就得到一个边长为7个单位长度的正方形,这时正方形C的面积就为(49-1)÷2+1=25个单位面积.
图5与图4同理.
我们从上表不难发现16+9=25,4+9=13即C的面积=A的面积+B的面积.
[师]图4和图5中的三个正方形A,B,C也是由中间的直角三角形“长”出来的,你能从三个正方形的面积关系与直角三角形的三边联系吗?
[生]图4中的正方形A,B,C的面积分别是直角三角形两条直角边的平方和斜边的平方,根据三个正方形的面积关系,我们不难发现,在这个直角三角形中,两条直角边的平方和等于斜边的平方.由图5我们也可得出同样的结论.
3.议一议
[师]我们通过对前面几个直角三角形的讨论,分析,你能归纳出直角三角形三边长度存在的关系吗?用自己的语言表达你的重大发现与同伴交流.
[生]在直角三角形中,两条直角边长度的平方和等于斜边的平方.
[师]这是由前面几个特例猜想出来的,是否合理呢?我们不妨作几个直角三角形检验一下.例如,作一个分别以5厘米、12厘米为直角边的直角三角形,然后测量斜边的长度,通过计算看一下直角三角形三边的规律还成立吗?
[生]1.作一个直角∠MCN;
2.以C为圆心,分别以5厘米、12厘米为半径画弧交CM、CN于点A,B;
3.连结AB.
用刻度尺量出斜边AB的长度(强调注意测量的误差)为13厘米.经检验斜边AB2=132=169,两直角边平方和AC2+BC2=52+122=25+144=169.即两直角边的平方和等于斜边的平方.
[师]很好.同学们不妨多作几个不同的直角三角形,用上面的方法检验直角三角形三边的关系.
[师生共析]通过特例猜想、检验,我们不难发现,直角三角形的三边的规律是成立的,这就是我们将要介绍的重点内容——勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2即直角三角形两直角边的平方和等于斜边的平方.
4.读一读(课本P5)
古代人就对勾股定理有过深入的研究,几大文明古国都有相应的勾股定理的记载.我国是最早发现勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角.如果勾(即直角三角形中较短的直角边)等于3,股(即直角三角形中较长的直角边)等于4,那么弦(即直角三角形中的斜边)等于5,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中,在这本书中的另一处,还记载了勾股定理的一般形式.因此,我们也把勾股定理称为商高定理,而把商高称为“勾股先师”.在西方,把勾股定理又称为“毕达哥拉斯”定理.相传二千多年,希腊著名数学家毕达哥拉斯学派首先证明了勾股定理,因此他们还举行了一次空前规模的庆祝活动,宰杀了一百头牲畜.但因此也引发了数学的第一次危机——边长为1的正方形的对角线的长度不能用整数或分数来表示.
关于勾股定理的记载还有很多,同学们如果有兴趣,可查阅有关这方面的资料。[来源:21世纪教育网]
所以说勾股定理有着悠久的历史,它反映了古代人民的聪明才智.
5.想一想
[师]小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的荧屏后,发现荧屏只有58厘米长和46厘米宽,他觉得一定是售货员搞错了,你同意他的想法吗?你能解释这是为什么吗?
[生]我听爸爸说过,29英寸或74厘米的电视机,是指荧屏对角线的长度,而不是其长或宽.21世纪教育网
[生]可是,连结荧屏的对角线将长方形的荧屏分成全等的两个直角三角形.根据勾股定理,长2+宽2=742,可582+462≠742,这是为什么呢?
[生]因为荧屏边框遮盖了一部分,所以实际测量存在一些误差.
[师]的确如此,但这里我们要知道一个生活常识,29英寸(74厘米)指的是荧屏的对角线的长度,而非荧屏的长或宽.
6.例题讲解
[例]在△ABC中,∠C=90°
(1)若a=8,b=6,则c=_________;
(2)若 c=20,b=12,则a=_________;
(3)若a∶b=3∶4,c=10,则a=_________,b=_________.
[师生共析]
分析:在△ABC中,∠C=90°,所以有关系:a2+b2=c2.在此关系式中,涉及到三个量,利用方程的思想,可“知二求一”.
解:根据题意可得a2+b2=c2.[来源:21世纪教育网]
(1)若a=8,b=6,所以82+62=c2.即c2=100,c>0,所以c=10;
(2)若c=20,b=12,所以a2+122=202,即a2=202-122=(20+12)(20-12)=32×8=162,a>0,所以a=16;
(3)若a∶b=3∶4,可设a=3x,b=4x,所以(3x)2+(4x)2=102.化简,得9x2+16x2=100,25x2=100,x2=4,x=2(x>0),所以a=3x=6;b=4x=8.
评注:综合上述解法可以发现,形(即△ABC为直角三角形)与数(a2+b2=c2)的统一,所以我们说勾股定理是形与数的结合.
Ⅲ.课时小结
先由学生自己总结,然后师生共同完成.这节课我们主要研究:
1.从特例猜想出勾股定理;21世纪教育网
2.用特例检验了勾股定理;
3.简单了解了勾股定理的历史,应用.
Ⅳ.课后作业
1.课本P30,习题2.1.
2.到网上或图书室查阅关于勾股定理的资料.
Ⅴ.活动与探究
有一根70 cm的木棒,要放在长、宽、高分别是50 cm、40 cm、30 cm的木箱中,能放进去吗?
过程:在实际生活中,往往工程设计方案比较多,应用所学的知识进行计算方可解决,而此题正是需要我们大胆实践和创新,用我们学过的勾股定理和丰富的空间想像力来解决.我们可注意到木棒虽比木箱的各边都长,按各边的大小放不进去,但木箱是立体图形,可以利用空间的最长长度.如AC′.
结果:由下图可得,AA′=30 cm,A′B′=50 cm,B′C′=40 cm.△A′B′C′, △AA′C′都为直角三角形.由勾股定理,得A′C′2=A′B′2+B′C′2.在Rt△AA′C′中.AC′最长,则AC′2=AA′2+A′B′2+B′C′2=302+402+502=5000>702.
故70 cm的棒能放入长、宽、高分别为50 cm,40 cm,30 cm的大箱中.
六.板书设计
§2.1 探索勾股定理(一)特例(做一做)勾股定理特例(议一议)(直角三角形两直角边分别为a,b,斜边为c,则a2+b2=c2)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2.1探索勾股定理
一.教学目标
(一)知识点
1.体验勾股定理的探索过程,由特例猜想勾股定理,再由特例验证勾股定理.
2.会利用勾股定理解释生活中的简单现象.
(二)能力训练要求
1.在学生充分观察、归纳、猜想、探索勾股定理的过程中,发展合情推理能力,体会数形结合的思想.
2.在探索勾股定理的过程中,发展学生归纳、概括和有条理地表达活动过程及结论的能力.
(三)情感与价值观要求
1.培养学生积极参与、合作交流的意识.
2.在探索勾股定理的过程中,体验获得成功的快乐,锻炼学生克服困难的勇气.
二.教学重、难点
重点:探索和验证勾股定理.
难点:在方格纸上通过计算面积的方法探索勾股定理.
三.教学方法
交流—探索—猜想.
在方格纸上,同学们通过计算以直角三角形的三边为边长的三个正方形的面积,在合作交流的过程中,比较这三个正方形的面积,由此猜想出直角三角形的三边关系.
四.教具准备
1.学生每人课前准备若干张方格纸.
2.投影片三张:
第一张:填空(记作§2.1 A);
第二张:问题串(记作§2.1 B);
第三张:做一做(记作§2.1 C).
五.教学过程
Ⅰ.创设问题情境,引入新课
出示投影片(§2.1 A)
(1)三角形按角分类,可分为_________、_________、_________.(2)对于一般的三角形来说,判断它们全等的条件有哪些?对于直角三角形呢?(3)有两个直角三角形,如果有两条边对应相等,那么这两个直角三角形一定全等吗?
[师]上面三个小问题是我们以前讨论过的,我们简单的回忆一下.
[生](1)三角形按角的大小来分类可分为:直角三角形、锐角三角形、钝角三角形;
(2)对于一般三角形来说,我们可以用SAS(边角边)、ASA(角边角)、AAS(角角边)、SSS(边边边)来判断两个三角形全等;而对于直角三角形来说,除以上四种方法外,还可以用HL(即有斜边和一条直角边对应相等的两个直角三角形全等).
(3)两个直角三角形,有两边对应相等,有两种情况:
第一种情况:两条直角边对应相等,这时,我们可注意到它们的夹角也对应相等,利用SAS可判断它们全等.
第二种情况:一条直角边和斜边对应相等,利用HL公理即可判断它们全等.
综上所述,两个直角三角形,如果有两边对应相等,则这两个直角三角形全等.
[师]我们可以注意到直角三角形有它独有的一些特征.在我们学习和生活中,你是否还发现直角三角形的其他特征呢?
这节课,我们就来继续研究直角三角形.
Ⅱ.讲述新课
1.问题串
[师](出示投影片§2.1 B)[来源:21世纪教育网]
观察下图,并回答问题:[来源:21世纪教育网](1)观察图1.正方形A中含有_________个小方格,即A的面积是_________个单位面积;正方形B中含有_________个小方格,即B的面积是_________个单位面积;正方形C中含有_________个小方格,即C的面积是_________个单位面积.21世纪教育网(2)在图2、图3中,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流.(3)请将上述结果填入下表,你能发现正方形A,B,C的面积关系吗?21世纪教育网A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图1图2图321世纪教育网
[生]在图1中,正方形A含1个小方格,所以它的面积是1个单位面积;正方形B含1个小方格,所以B的面积也是1个单位面积;正方形C含2个小方格,所以C的面积是2个单位面积.
[师]如何求得正方形C的面积呢?
[生]正方形C可划分为四个直角边长都为1个单位的四个全等的等腰直角三角形,所以C的面积为4×(×1×1)=2个单位面积.
[生]我们观察可发现,这四个等腰直角三角形重新拼摆,刚好可拼摆成2个小方格,所以C的面积为2个单位面积.
[生]正方形C还可以看成边长为2个单位的正方形面积的一半,即C的面积为×22=2个单位面积.
[师]同学们能够不拘一格地积极思考问题,用多种方法去求得图1中C的面积,值得发扬广大,那么图2,图3中的A,B,C的面积是否可借鉴图1中的A,B,C的求法获得呢?请与你的同学们讨论、交流。
[生]图2中,A含有9个小方格或者说正方形A的边长是3个单位长度,都可以求得A的面积是9个单位面积;同理可求得B含有9个小方格,所以B的面积为9个单位面积;对于正方形C来说,我们观察可发现它含有18个小方格,所以C的面积为18个单位面积.
[师]看来,同学们已能从图2中很容易地就求得了A,B,C的面积.是不是在求C的面积时也和图1相类似,有多种求法呢?
[生]是的.在正方形C中,我们可以把它的边缘的12个全等的等腰直角三角形拼摆成6个小方格,再加上中间的12个小方格,正方形C共含有18个小方格,所以它的面积为18个单位面积;我们也可以把C分割成四个直角边为3个单位长度的等腰直角三角形,也可算得C的面积为4×(×32)=18个单位面积.
[生]如果把组成C的四个等腰直角三角形沿正方形的边向外翻,我们观察又可发现C在边长为6个单位长度的正方形中,并且C的面积恰好是这个正方形面积的一半即×62=18个单位面积.
[生]图3与图1,图2类似,所以我们可用同样的方法观察求得A,B,C各含4个,4个,8个小方格,面积分别为4个,4个,8个单位面积.
[师]把三个图中A,B,C的面积分别填入上面的表格中,你能发现它们的关系吗?
[生]C的面积=A的面积+B的面积.
(表格略)21世纪教育网
[师]很好!但是A,B,C的面积为什么会有这种关系呢?我们接着观察这三个图,你能发现什么?
[生]在前面您说过这节课我们主要研究直角三角形,而在这三个图中,都是三个正方形围着一个直角三角形.
[师]的确如此,从图中我们可以发现:三个正方形好像是“长”在直角三角形的三边上.
[生]这说明三个正方形的边长分别是以直角三角形的三边为边长得到的.
[师]那么,(3)的结论即C的面积=A的面积+B的面积与三角形有什么关系?这个关系说明什么?大家可以讨论、交流.
[生]C是斜边上的正方形,所以C的面积是斜边的平方;A,B是两直角边上的正方形,所以A,B的面积分别是这两条直角边的平方.根据A,B,C的面积关系,我们不难发现:斜边的平方就等于两直角边的平方和.
[师]但是,我们也不难发现上面3个图中的直角三角形是等腰直角三角形?如果不是等腰直角三角形,而是一般的直角三角形,会不会也有这种三边关系呢?
2.做一做
出示投影片(§2.1 C)
(1)观察图4,图5,并填写下表:A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图4[来源:21世纪教育网]图5你是怎样得到上面结果的?与同伴交流.(2)三个正方形A,B,C的面积之间的关系?
(让学生先独立思考,然后填写上面的表格.最后以小组为单位充分交流各自的想法,特别是在计算斜边上的正方形的面积即正方形C的求法)
[师生共析]根据图4,图5可填表如下:
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)
图4 16 9 25
图5 4 9 1321世纪教育网
我们先来观察图4,不难看出A,B分别含有16个小方格,9个小方格,所以A、B的面积分别为16个单位面积,9个单位面积,但斜边上的正方形C的面积的计算较为复杂,我们可用以下几种方法求得:
第一种方法:将正方形C分割成4个直角边长分别为3、4全等的直角三角形和中间的一个小方格,利用计算三角形面积的公式可得正方形C的面积为4×(×3×4)+1=24+1=25个单位面积.
第二种方法:直接数正方形C中含有多少个小方格,但需要适当的拼凑,在第一种方法中,我们将正方形分割成5部分,直角三角形Ⅰ、Ⅱ、Ⅲ、Ⅳ和一个小方格,其中直角三角形Ⅰ、Ⅲ可拼凑成一个长和宽分别为3和4的长方形,含有12个小方格,同理Ⅱ、Ⅳ也可拼凑成12个小方格,所以正方形C中共有12+12+1=25个小方格即C的面积为25个单位面积.
第三种方法:可将直角三角形Ⅰ、Ⅱ、Ⅲ、Ⅳ沿正方形C的边外翻,就得到一个边长为7个单位长度的正方形,这时正方形C的面积就为(49-1)÷2+1=25个单位面积.
图5与图4同理.
我们从上表不难发现16+9=25,4+9=13即C的面积=A的面积+B的面积.
[师]图4和图5中的三个正方形A,B,C也是由中间的直角三角形“长”出来的,你能从三个正方形的面积关系与直角三角形的三边联系吗?
[生]图4中的正方形A,B,C的面积分别是直角三角形两条直角边的平方和斜边的平方,根据三个正方形的面积关系,我们不难发现,在这个直角三角形中,两条直角边的平方和等于斜边的平方.由图5我们也可得出同样的结论.
3.议一议
[师]我们通过对前面几个直角三角形的讨论,分析,你能归纳出直角三角形三边长度存在的关系吗?用自己的语言表达你的重大发现与同伴交流.
[生]在直角三角形中,两条直角边长度的平方和等于斜边的平方.
[师]这是由前面几个特例猜想出来的,是否合理呢?我们不妨作几个直角三角形检验一下.例如,作一个分别以5厘米、12厘米为直角边的直角三角形,然后测量斜边的长度,通过计算看一下直角三角形三边的规律还成立吗?
[生]1.作一个直角∠MCN;
2.以C为圆心,分别以5厘米、12厘米为半径画弧交CM、CN于点A,B;
3.连结AB.
用刻度尺量出斜边AB的长度(强调注意测量的误差)为13厘米.经检验斜边AB2=132=169,两直角边平方和AC2+BC2=52+122=25+144=169.即两直角边的平方和等于斜边的平方.
[师]很好.同学们不妨多作几个不同的直角三角形,用上面的方法检验直角三角形三边的关系.
[师生共析]通过特例猜想、检验,我们不难发现,直角三角形的三边的规律是成立的,这就是我们将要介绍的重点内容——勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2即直角三角形两直角边的平方和等于斜边的平方.
4.读一读(课本P5)
古代人就对勾股定理有过深入的研究,几大文明古国都有相应的勾股定理的记载.我国是最早发现勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角.如果勾(即直角三角形中较短的直角边)等于3,股(即直角三角形中较长的直角边)等于4,那么弦(即直角三角形中的斜边)等于5,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中,在这本书中的另一处,还记载了勾股定理的一般形式.因此,我们也把勾股定理称为商高定理,而把商高称为“勾股先师”.在西方,把勾股定理又称为“毕达哥拉斯”定理.相传二千多年,希腊著名数学家毕达哥拉斯学派首先证明了勾股定理,因此他们还举行了一次空前规模的庆祝活动,宰杀了一百头牲畜.但因此也引发了数学的第一次危机——边长为1的正方形的对角线的长度不能用整数或分数来表示.
关于勾股定理的记载还有很多,同学们如果有兴趣,可查阅有关这方面的资料。[来源:21世纪教育网]
所以说勾股定理有着悠久的历史,它反映了古代人民的聪明才智.
5.想一想
[师]小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的荧屏后,发现荧屏只有58厘米长和46厘米宽,他觉得一定是售货员搞错了,你同意他的想法吗?你能解释这是为什么吗?
[生]我听爸爸说过,29英寸或74厘米的电视机,是指荧屏对角线的长度,而不是其长或宽.21世纪教育网
[生]可是,连结荧屏的对角线将长方形的荧屏分成全等的两个直角三角形.根据勾股定理,长2+宽2=742,可582+462≠742,这是为什么呢?
[生]因为荧屏边框遮盖了一部分,所以实际测量存在一些误差.
[师]的确如此,但这里我们要知道一个生活常识,29英寸(74厘米)指的是荧屏的对角线的长度,而非荧屏的长或宽.
6.例题讲解
[例]在△ABC中,∠C=90°
(1)若a=8,b=6,则c=_________;
(2)若 c=20,b=12,则a=_________;
(3)若a∶b=3∶4,c=10,则a=_________,b=_________.
[师生共析]
分析:在△ABC中,∠C=90°,所以有关系:a2+b2=c2.在此关系式中,涉及到三个量,利用方程的思想,可“知二求一”.
解:根据题意可得a2+b2=c2.[来源:21世纪教育网]
(1)若a=8,b=6,所以82+62=c2.即c2=100,c>0,所以c=10;
(2)若c=20,b=12,所以a2+122=202,即a2=202-122=(20+12)(20-12)=32×8=162,a>0,所以a=16;
(3)若a∶b=3∶4,可设a=3x,b=4x,所以(3x)2+(4x)2=102.化简,得9x2+16x2=100,25x2=100,x2=4,x=2(x>0),所以a=3x=6;b=4x=8.
评注:综合上述解法可以发现,形(即△ABC为直角三角形)与数(a2+b2=c2)的统一,所以我们说勾股定理是形与数的结合.
Ⅲ.课时小结
先由学生自己总结,然后师生共同完成.这节课我们主要研究:
1.从特例猜想出勾股定理;21世纪教育网
2.用特例检验了勾股定理;
3.简单了解了勾股定理的历史,应用.
Ⅳ.课后作业
1.课本P30,习题2.1.
2.到网上或图书室查阅关于勾股定理的资料.
Ⅴ.活动与探究
有一根70 cm的木棒,要放在长、宽、高分别是50 cm、40 cm、30 cm的木箱中,能放进去吗?
过程:在实际生活中,往往工程设计方案比较多,应用所学的知识进行计算方可解决,而此题正是需要我们大胆实践和创新,用我们学过的勾股定理和丰富的空间想像力来解决.我们可注意到木棒虽比木箱的各边都长,按各边的大小放不进去,但木箱是立体图形,可以利用空间的最长长度.如AC′.
结果:由下图可得,AA′=30 cm,A′B′=50 cm,B′C′=40 cm.△A′B′C′, △AA′C′都为直角三角形.由勾股定理,得A′C′2=A′B′2+B′C′2.在Rt△AA′C′中.AC′最长,则AC′2=AA′2+A′B′2+B′C′2=302+402+502=5000>702.
故70 cm的棒能放入长、宽、高分别为50 cm,40 cm,30 cm的大箱中.
六.板书设计
§2.1 探索勾股定理(一)特例(做一做)勾股定理特例(议一议)(直角三角形两直角边分别为a,b,斜边为c,则a2+b2=c2)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
