(沪教版高一)数学:3.4《函数单调性》课件
文档属性
| 名称 | (沪教版高一)数学:3.4《函数单调性》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 202.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-10 16:22:00 | ||
图片预览






文档简介
课件17张PPT。函数单调性
回顾 1、函数的单调性的定义. 2、判断、证明函数的单调性方法.3、用定义法证明函数单调性的步骤:①取值; ②作差变形; ③定号; ④下结论
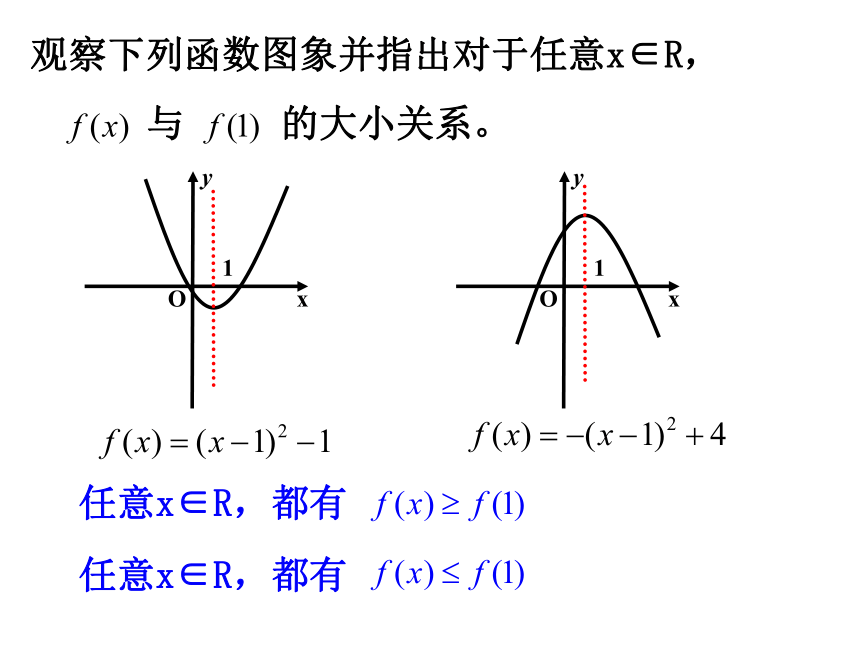
.观察下列函数图象并指出对于任意x∈R,
与 的大小关系。xyO1xyO1任意x∈R,都有任意x∈R,都有函数最大值一般地,设 的定义域为A.如果存在x0∈A,使得对于任意的x∈A,
都有
那么称 为 的最大值,
记为
函数最小值讨论 设函数 的定义域为[a,b],(1)若 是增函数,则
, . (2)若 是减函数,则
, . 讨论 判断下列说法是否正确(1)单调函数一定有最大值和最小值.(2)在定义域内不具有单调性的函数一定没有最大值和最小值. 例2.求下列函数的最值.问题讨论1、求下列函数的单调区间,如图,如图xyO23-1xyO31 2、若函数 在
上是增函数,在 上是减函数,则
实数m的值为 ; 变:若函数 在
上是增函数,则实数m的范围为 ; 变:若函数 的单调
递增区间为 ,则实数m的值为 .-16m≤-16-163、若定义在R上的单调减函数 满足 ,你知道 的取值范围吗?变:若定义在R上的函数 对任意的正数
都有 ,求满足
的 的取值范围。变:若定义域改为(-1,1)呢?小结 1、函数的单调性的定义. 2、判断、证明函数的单调性方法. 3、函数的单调性的应用.思考若 为定义在数集A上的增函数,
且 ,试判断下列函数的单调性:
.观察下列函数图象并指出对于任意x∈R,
与 的大小关系。xyO1xyO1任意x∈R,都有任意x∈R,都有函数最大值一般地,设 的定义域为A.如果存在x0∈A,使得对于任意的x∈A,
都有
那么称 为 的最大值,
记为
函数最小值讨论 设函数 的定义域为[a,b],(1)若 是增函数,则
, . (2)若 是减函数,则
, . 讨论 判断下列说法是否正确(1)单调函数一定有最大值和最小值.(2)在定义域内不具有单调性的函数一定没有最大值和最小值. 例2.求下列函数的最值.问题讨论1、求下列函数的单调区间,如图,如图xyO23-1xyO31 2、若函数 在
上是增函数,在 上是减函数,则
实数m的值为 ; 变:若函数 在
上是增函数,则实数m的范围为 ; 变:若函数 的单调
递增区间为 ,则实数m的值为 .-16m≤-16-163、若定义在R上的单调减函数 满足 ,你知道 的取值范围吗?变:若定义在R上的函数 对任意的正数
都有 ,求满足
的 的取值范围。变:若定义域改为(-1,1)呢?小结 1、函数的单调性的定义. 2、判断、证明函数的单调性方法. 3、函数的单调性的应用.思考若 为定义在数集A上的增函数,
且 ,试判断下列函数的单调性:
