(沪教版高一)数学:4.2《幂函数的性质》课件
文档属性
| 名称 | (沪教版高一)数学:4.2《幂函数的性质》课件 |
|
|
| 格式 | rar | ||
| 文件大小 | 267.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-10 16:18:00 | ||
图片预览






文档简介
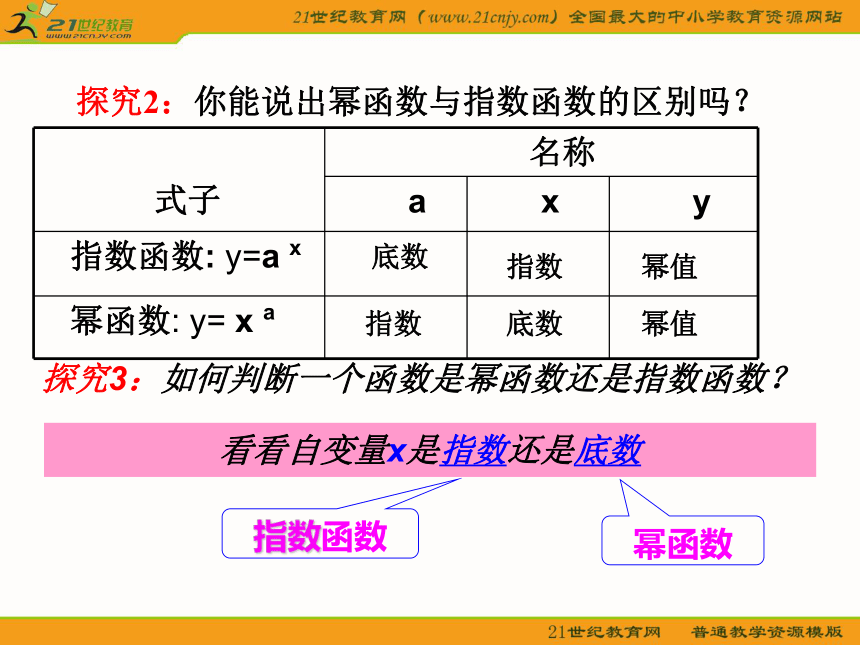
课件14张PPT。幂 函 数问题引入:1、如果张红购买了每千克1元的蔬菜x千克, 则所需的钱数y=____元.2、如果正方形的边长为x,则面积y=_____.xx24、如果一个正方形场地的面积为x,边长为那么y=______.5、如果某人x 秒内骑车行进了1公里,骑车的速度为y公里/秒,那么y=______x3?以上问题中的函数具有什么共同特征?y = x3y = xy = x2 共同特征:函数解析式是幂的形式,且指数是常数,底数是自变量。新课一、幂函数的概念探究1:你能举几个学过的幂函数的例子吗? 一般地,函数 叫做幂函数,其中x是自变量, 是常数。底数指数指数底数幂值幂值探究3:如何判断一个函数是幂函数还是指数函数?看看自变量x是指数还是底数幂函数指数函数探究2:你能说出幂函数与指数函数的区别吗? 1、下面几个函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=x2 + x (4)
(5)y = 2x 答案(1)(4)尝 试 练 习: 2、已知幂函数y = f (x)的图象经过点(3 , ),求这个函数的解析式。待定系数法 3、如果函数
f (x) = (m2-m-1) 是幂函数,
求实数m的值。
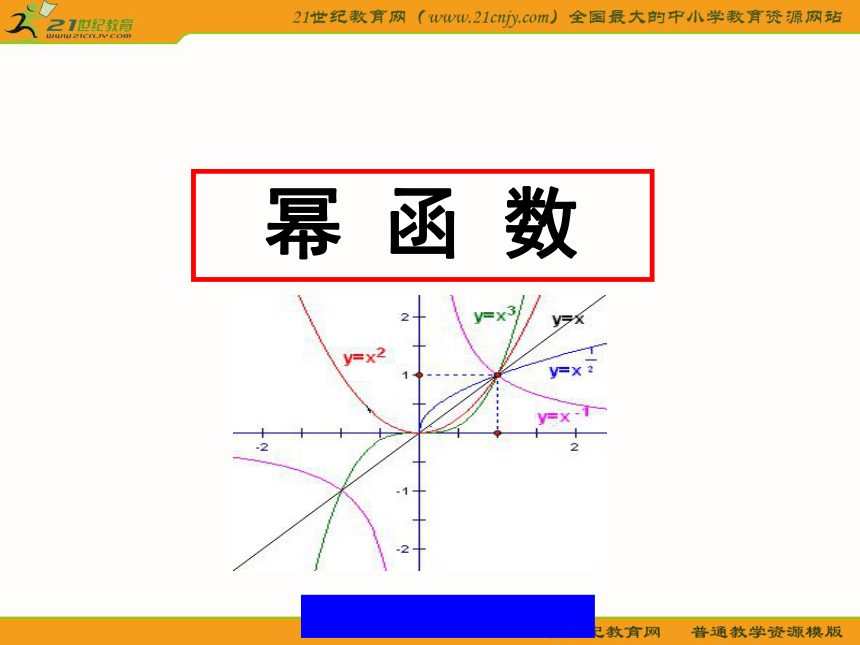
m= -1 或 m= 2 对于幂函数,我们只讨论α=1,2,3, ,–1 时的情形。二、幂函数性质的探究:探究4:结合前面指数函数与对数函数的方法,我们应如何研究幂函数呢?作具体幂函数的图象→观察图象特征→总结函数性质探究5:在同一坐标系中作出幂函数
的图象。探究6: (探究性质)请同学们结合幂函数图象(课本第86页图2.3.1),将你发现的结论填在下面(课本第86页) 的表格内:y = xRRR[0,+∞){x| x ≠ 0}R[0,+∞)R[0,+∞){y| y≠ 0}奇函数偶函数奇函数非奇非偶函数奇函数
R上是
增函数在(-∞,0]上是减函数,在[0, +∞)上是增函数R上是增函数在[0,+∞)上是增函数在( -∞,0)和(0, +∞)上是减函数(1,1)奇偶性y = x2(1)所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1); 例1、证明幂函数 在 上是
增函数。收 获 与 体 会 请大家回味建立幂函数模型、定义幂函数及推导幂函数性质的过程,你觉得有什么收获?
(1)y = (2)y=2x2
(3)y=x2 + x (4)
(5)y = 2x 答案(1)(4)尝 试 练 习: 2、已知幂函数y = f (x)的图象经过点(3 , ),求这个函数的解析式。待定系数法 3、如果函数
f (x) = (m2-m-1) 是幂函数,
求实数m的值。
m= -1 或 m= 2 对于幂函数,我们只讨论α=1,2,3, ,–1 时的情形。二、幂函数性质的探究:探究4:结合前面指数函数与对数函数的方法,我们应如何研究幂函数呢?作具体幂函数的图象→观察图象特征→总结函数性质探究5:在同一坐标系中作出幂函数
的图象。探究6: (探究性质)请同学们结合幂函数图象(课本第86页图2.3.1),将你发现的结论填在下面(课本第86页) 的表格内:y = xRRR[0,+∞){x| x ≠ 0}R[0,+∞)R[0,+∞){y| y≠ 0}奇函数偶函数奇函数非奇非偶函数奇函数
R上是
增函数在(-∞,0]上是减函数,在[0, +∞)上是增函数R上是增函数在[0,+∞)上是增函数在( -∞,0)和(0, +∞)上是减函数(1,1)奇偶性y = x2(1)所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1); 例1、证明幂函数 在 上是
增函数。收 获 与 体 会 请大家回味建立幂函数模型、定义幂函数及推导幂函数性质的过程,你觉得有什么收获?
