(沪教版高二)数学:8.2《平面向量的数量积》课件
文档属性
| 名称 | (沪教版高二)数学:8.2《平面向量的数量积》课件 |
|
|
| 格式 | rar | ||
| 文件大小 | 539.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-10 16:21:00 | ||
图片预览









文档简介
课件33张PPT。向量的数量积问题1:我们学习了向量的哪些运算?
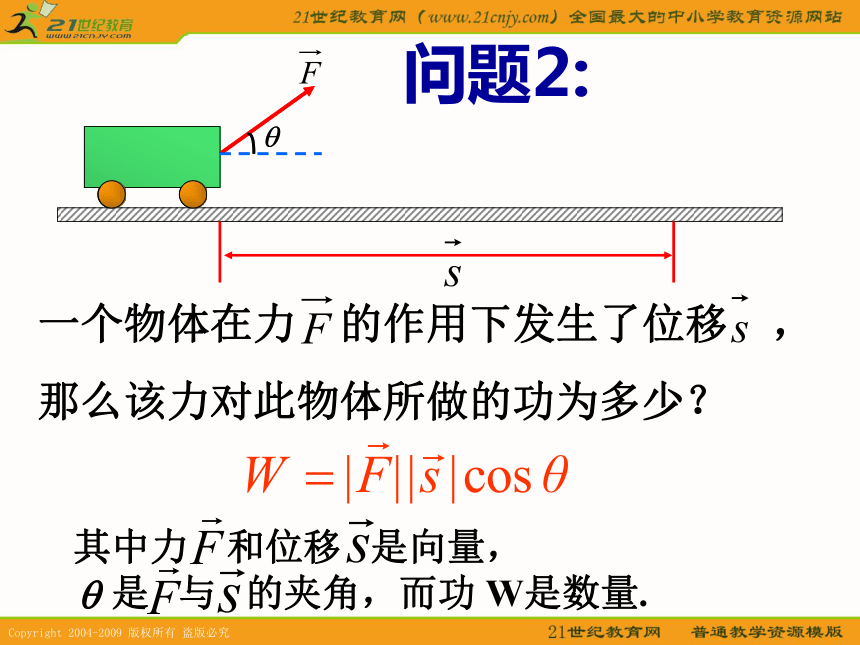
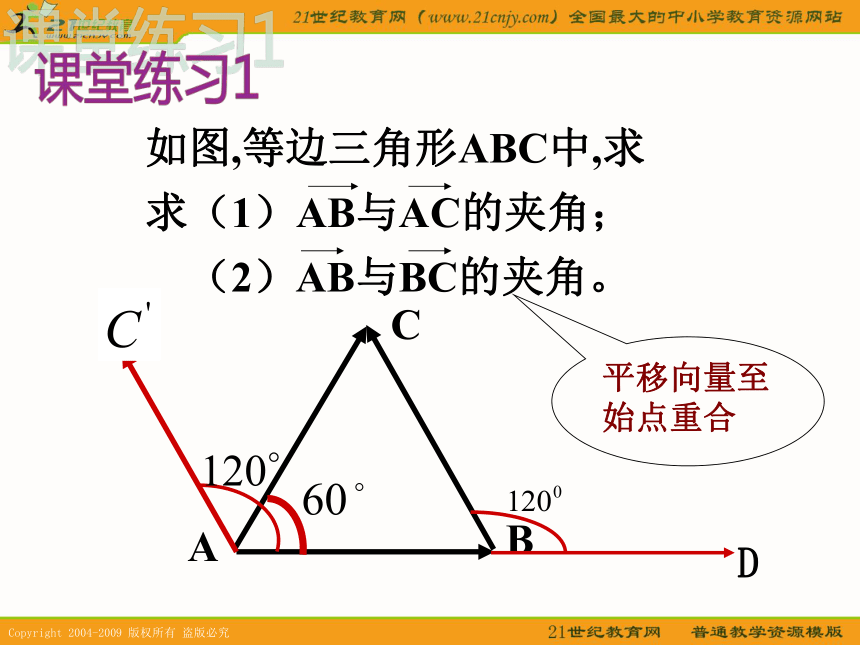
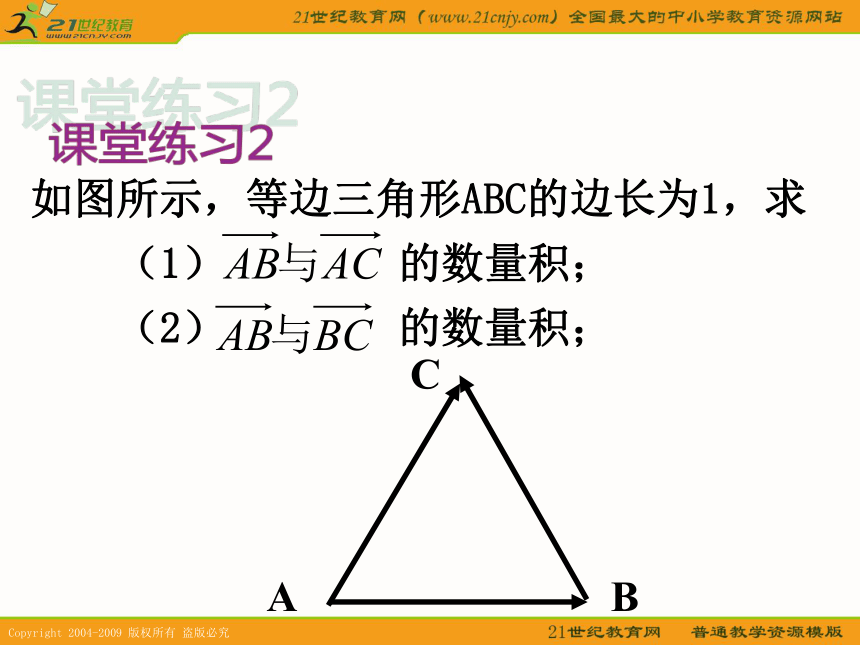
这些运算的结果是什么?平面向量的加法、减法和数乘三种运算;运算的结果仍是向量问题2:将公式中的力与位移推广到一般向量功是力与位移的大小及其夹角余弦的乘积; 结果是两个向量的模及其夹角余弦的乘积。出现了向量的一种新的运算1、向量的夹角规定:零向量与其它向量的夹角可根据需要确定。课堂练习1D2、向量的数量积的定义 2、向量的数量积是一个数量,不是向量。向量的数量积的说明如图所示,等边三角形ABC的边长为1,求
(1) 的数量积;
(2) 的数量积; ABC课堂练习23、向量的数量积的重要性质两个重要的充要条件3、向量的数量积的重要性质1350直角例2、填空( × )(×)( √ )( √ )( × )课堂练习3课堂练习3DC问题:(1)实数乘法有哪些运算律?(2)这些运算律是否能适用于
向量的数量积的运算? 4、向量的数量积的运算律实数乘法向量的数量积类比猜想是否都成立?验证向量数量积的运算律思考:即:向量数量积运算不满足结合律若如何验证?或通过向量数量积的坐标表示验证。可借助向量数量积的几何意义验证;5、向量的数量积的几何意义(B1)5、向量的数量积的几何意义(1)投影是一个数量,不是向量。5、向量的数量积的几何意义5、向量的数量积的几何意义用向量的几何意义验证向量的数量积的常用公式例3、证明(5)(3) (6)(4)
(7)课堂练习4例6、用向量方法证明:
径所对的圆周角为直角。如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点。求证∠ACB=90°分析:要证∠ACB=90°,只须证向
量 ,即 。解:设
则 ,
由此可得:五、小结1、向量的夹角2、向量数量积的定义3、向量数量积的性质4、向量数量积的运算律
这些运算的结果是什么?平面向量的加法、减法和数乘三种运算;运算的结果仍是向量问题2:将公式中的力与位移推广到一般向量功是力与位移的大小及其夹角余弦的乘积; 结果是两个向量的模及其夹角余弦的乘积。出现了向量的一种新的运算1、向量的夹角规定:零向量与其它向量的夹角可根据需要确定。课堂练习1D2、向量的数量积的定义 2、向量的数量积是一个数量,不是向量。向量的数量积的说明如图所示,等边三角形ABC的边长为1,求
(1) 的数量积;
(2) 的数量积; ABC课堂练习23、向量的数量积的重要性质两个重要的充要条件3、向量的数量积的重要性质1350直角例2、填空( × )(×)( √ )( √ )( × )课堂练习3课堂练习3DC问题:(1)实数乘法有哪些运算律?(2)这些运算律是否能适用于
向量的数量积的运算? 4、向量的数量积的运算律实数乘法向量的数量积类比猜想是否都成立?验证向量数量积的运算律思考:即:向量数量积运算不满足结合律若如何验证?或通过向量数量积的坐标表示验证。可借助向量数量积的几何意义验证;5、向量的数量积的几何意义(B1)5、向量的数量积的几何意义(1)投影是一个数量,不是向量。5、向量的数量积的几何意义5、向量的数量积的几何意义用向量的几何意义验证向量的数量积的常用公式例3、证明(5)(3) (6)(4)
(7)课堂练习4例6、用向量方法证明:
径所对的圆周角为直角。如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点。求证∠ACB=90°分析:要证∠ACB=90°,只须证向
量 ,即 。解:设
则 ,
由此可得:五、小结1、向量的夹角2、向量数量积的定义3、向量数量积的性质4、向量数量积的运算律
