(沪教版高三上)数学:15.5《空间几何体的体积》课件(2)
文档属性
| 名称 | (沪教版高三上)数学:15.5《空间几何体的体积》课件(2) |  | |
| 格式 | rar | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-10 16:21:00 | ||
图片预览








文档简介
课件32张PPT。笛卡儿说:“数学是知识的工具,
亦是其它知识工具的泉源。
所有研究顺序和度量的科学
均和数学有关。” 青藏铁路是西部大开发标志性工程,
全长1142公里,是世界上海拔最高,
线路最长,穿越冻土里程最长的高原铁路。青藏铁路假设在青藏铁路的某段路基需要用碎石铺垫.已知路基的形状尺寸如图所示(单位:米),问每修建1千米铁路需要碎石多少立方米?想知道如何求吗?
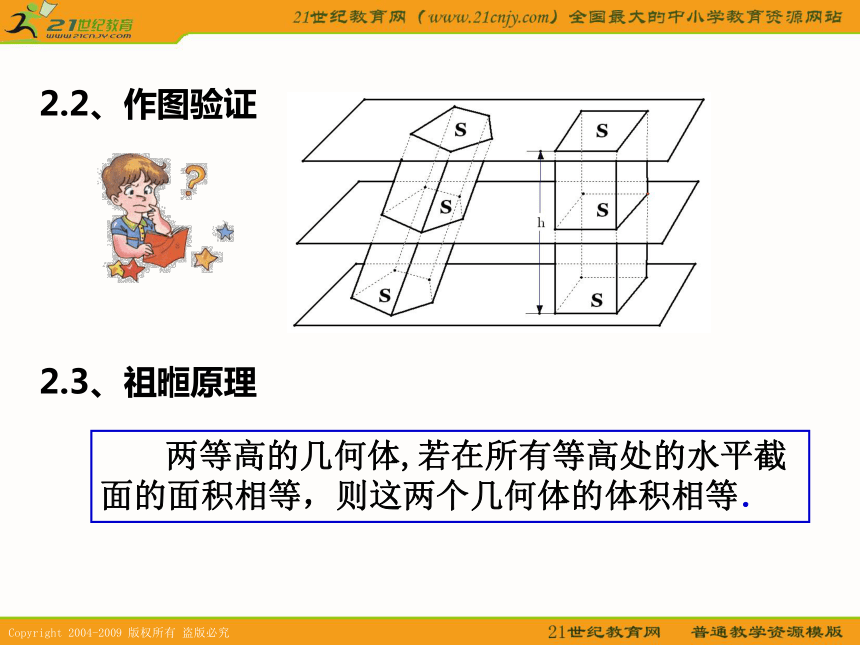
让我们一起来探索吧!空间几何体的体积 平面几何中我们用单位正方形的面积来度量平面图形的面积,立体几何中用单位正方体(棱长为1个长度单位)的体积来度量几何体的体积. 一个几何体的体积是单位正方体体积的多少倍,那么这个倍数就是这个几何体的体积的数值. 某长方体纸盒的长、宽、高分别为4cm,3cm,3cm,则每层有__________个单位正方体,三层共有____ 个单位正方体,所以,整个长方体的体积是_____4×3= 12 3636cm3问题1:长方体体积V长方体=abc或V长方体=sh(s,h分别表示长方体的底面积和高)(a,b,c分别为长方体长、宽、高) 取一摞书放在桌面上,并改变它们的位置,观察改变前后的体积是否发生变化?问题2:一般柱体的体积高度、书中每页纸面积和顺序不变2.1实验猜想:2.3、祖暅原理2.2、作图验证 两等高的几何体,若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等. 我国古代著名数学家祖冲之在计算圆周率等问题方面有光辉的成就。祖冲之的儿子祖暅也在数学上有突出贡献。祖暅在实践的基础上,于5世纪末提出了这个体积计算原理。
祖暅提出这个原理,要比其他国家的数学家早一千多年。在欧洲只道17世纪,才有意大利数学家卡瓦列里(Cavalieri .B,1598年--1647年)
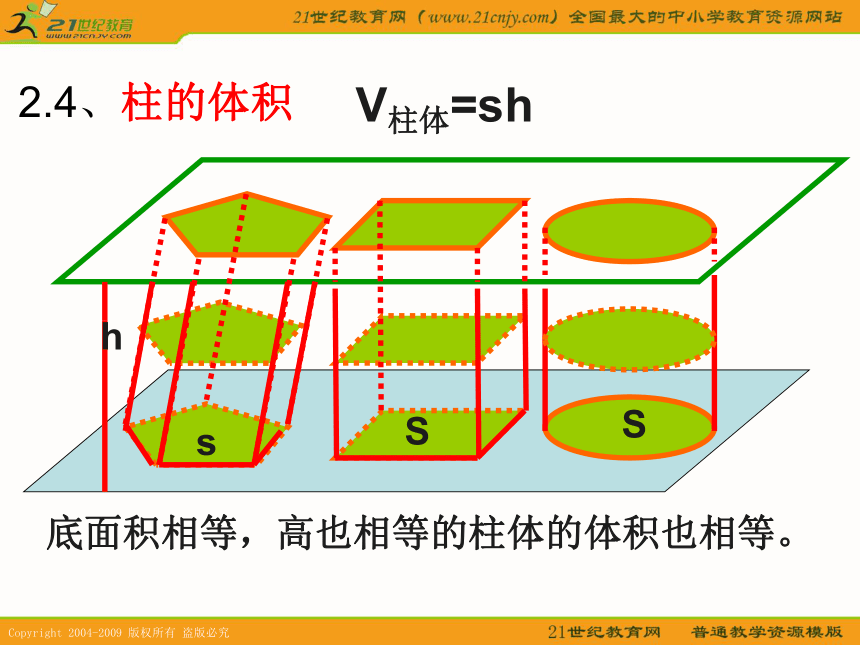
提出上述结论。 (429年~500年) 2.4、柱的体积shSS底面积相等,高也相等的柱体的体积也相等。V柱体=sh3.1.锥体(棱锥、圆锥)的体积
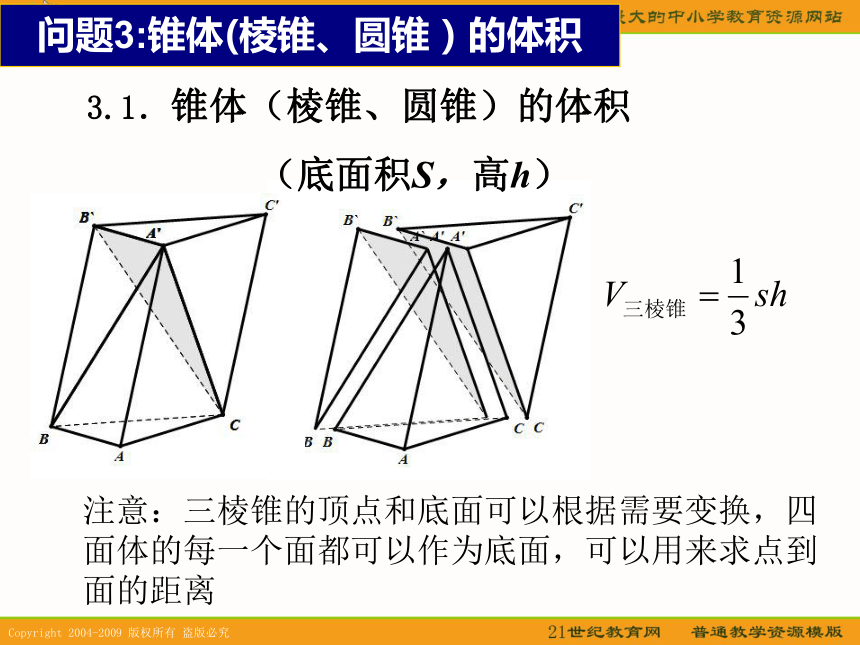
(底面积S,高h) 注意:三棱锥的顶点和底面可以根据需要变换,四面体的每一个面都可以作为底面,可以用来求点到面的距离问题3:锥体(棱锥、圆锥)的体积 类似的,底面积相等,高也相等的两个锥
体的体积也相等.V锥体=S为底面积,h为高.ss3.2等底面积等高的锥体的体积有何关系?hxV台体=上下底面积分别是s/,s,高是h,则问题4:台体(棱锥、圆锥)的体积V台体=V柱体=shV锥体=ss/sS/=0S=S’问题5:柱、锥、台的体积关系假设在青藏铁路的某段路基需要用碎石铺垫.已知路基的形状尺寸如图所示(单位:米),问每修建1千米铁路需要碎石多少立方米?例题探究例1. 一几何体按比例绘制的三视图如图所示,(单位:m)
(1)试画出它的直观图;(2)求它的体积。(2)底面积 s = ? ( 1 + 2 ) ? 1= 1.5 m2
几何体的体积 V= 1.5 ? 1= 1.5 m3例2、将边长为a的正方形ABCD沿对角线AC折起,使B,D两点间距离变为a,则所得三棱锥D-ABC的体积为ABCD例2、将边长为a的正方形ABCD沿对角线AC折起,使B,D两点间距离变为a,则所得三棱锥D-ABC的体积为ABCD你能求出A点到面BDC的距离吗?例3、有一堆相同规格的六角螺帽毛坯共重5.8kg.
已知底面六边形的边长是12mm,高是10mm,内孔直径是10mm,那么约有毛坯多少个?(铁的比重是7.8g/cm3)分析:六角螺帽毛坯的体积是一个
正六棱柱的体积与一个圆柱的体积的差.解:V正六棱柱=1.732×122×6×10≈3.74×103(mm3)
V圆柱=3.14×52×10≈0.785×103(mm3)
毛坯的体积V=3.74×103-0.785×103
≈2.96×103(mm3)=2.96(cm3)
约有毛坯:5.8×103÷(7.8×2.96)≈2.5×102(个)
答:这堆毛坯约有250个。2、用一张长12cm、宽8cm的铁皮围成圆柱形的侧面,该圆柱体积为 ______
(结果保留 )课堂练习1、已知一正四棱台的上底面边长为4cm,下底面边长为8cm,高为3cm,其体积为______112cm33、埃及胡夫金字塔大约建于公元前2580年,其形状为正四棱锥.金字塔高146.6米,底面边长230.4米.求这座金字塔的体积.V=2594046.0(m3)(2)柱、锥、台体积的计算公式及它们之间的联系(1)体积度量的基本思路:长方体体积公式是计算其他几何体体积的基础.问题6:回顾反思即特殊到一般的数学思想。RR球的体积:一个半径和高都等于R的圆柱,挖去一个
以上底面为底面,下底面圆心为顶点的圆锥
后,所得的几何体的体积与一个半径为R的
半球的体积相等。探究RRRS1探究球的表面积:球的表面积:设想一个球由许多顶点在球心,底面在球面上的“准锥体”组成,这些准锥体的底面并不是真的多边形,但只要其底面足够小,就可以把它们看成真正的锥体.1.一个正方体内接于半径为R的球内,求正方体的体积.2.一个平面截一个球得到直径是6cm的圆面,球心到这个平面的距离是4cm,求该球的表面积和体积.例: 如图是一个奖杯的三视图,单位是cm,
试画出它的直观图,并计算这个奖杯的体积.
(精确到0.01cm)86618515151111x/y/z/这个奖杯的体积为V=V正四棱台+V长方体+ V球
其中V正四棱台V正方体=6×8×18=864V球=所以这个奖杯的体积为V=1828.76cm3例2.已知一个正四面体内接一个表面积为36 的球内,求这个四面体的表面积和体积数学 因探索而精彩、 因应用而美丽!
亦是其它知识工具的泉源。
所有研究顺序和度量的科学
均和数学有关。” 青藏铁路是西部大开发标志性工程,
全长1142公里,是世界上海拔最高,
线路最长,穿越冻土里程最长的高原铁路。青藏铁路假设在青藏铁路的某段路基需要用碎石铺垫.已知路基的形状尺寸如图所示(单位:米),问每修建1千米铁路需要碎石多少立方米?想知道如何求吗?
让我们一起来探索吧!空间几何体的体积 平面几何中我们用单位正方形的面积来度量平面图形的面积,立体几何中用单位正方体(棱长为1个长度单位)的体积来度量几何体的体积. 一个几何体的体积是单位正方体体积的多少倍,那么这个倍数就是这个几何体的体积的数值. 某长方体纸盒的长、宽、高分别为4cm,3cm,3cm,则每层有__________个单位正方体,三层共有____ 个单位正方体,所以,整个长方体的体积是_____4×3= 12 3636cm3问题1:长方体体积V长方体=abc或V长方体=sh(s,h分别表示长方体的底面积和高)(a,b,c分别为长方体长、宽、高) 取一摞书放在桌面上,并改变它们的位置,观察改变前后的体积是否发生变化?问题2:一般柱体的体积高度、书中每页纸面积和顺序不变2.1实验猜想:2.3、祖暅原理2.2、作图验证 两等高的几何体,若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等. 我国古代著名数学家祖冲之在计算圆周率等问题方面有光辉的成就。祖冲之的儿子祖暅也在数学上有突出贡献。祖暅在实践的基础上,于5世纪末提出了这个体积计算原理。
祖暅提出这个原理,要比其他国家的数学家早一千多年。在欧洲只道17世纪,才有意大利数学家卡瓦列里(Cavalieri .B,1598年--1647年)
提出上述结论。 (429年~500年) 2.4、柱的体积shSS底面积相等,高也相等的柱体的体积也相等。V柱体=sh3.1.锥体(棱锥、圆锥)的体积
(底面积S,高h) 注意:三棱锥的顶点和底面可以根据需要变换,四面体的每一个面都可以作为底面,可以用来求点到面的距离问题3:锥体(棱锥、圆锥)的体积 类似的,底面积相等,高也相等的两个锥
体的体积也相等.V锥体=S为底面积,h为高.ss3.2等底面积等高的锥体的体积有何关系?hxV台体=上下底面积分别是s/,s,高是h,则问题4:台体(棱锥、圆锥)的体积V台体=V柱体=shV锥体=ss/sS/=0S=S’问题5:柱、锥、台的体积关系假设在青藏铁路的某段路基需要用碎石铺垫.已知路基的形状尺寸如图所示(单位:米),问每修建1千米铁路需要碎石多少立方米?例题探究例1. 一几何体按比例绘制的三视图如图所示,(单位:m)
(1)试画出它的直观图;(2)求它的体积。(2)底面积 s = ? ( 1 + 2 ) ? 1= 1.5 m2
几何体的体积 V= 1.5 ? 1= 1.5 m3例2、将边长为a的正方形ABCD沿对角线AC折起,使B,D两点间距离变为a,则所得三棱锥D-ABC的体积为ABCD例2、将边长为a的正方形ABCD沿对角线AC折起,使B,D两点间距离变为a,则所得三棱锥D-ABC的体积为ABCD你能求出A点到面BDC的距离吗?例3、有一堆相同规格的六角螺帽毛坯共重5.8kg.
已知底面六边形的边长是12mm,高是10mm,内孔直径是10mm,那么约有毛坯多少个?(铁的比重是7.8g/cm3)分析:六角螺帽毛坯的体积是一个
正六棱柱的体积与一个圆柱的体积的差.解:V正六棱柱=1.732×122×6×10≈3.74×103(mm3)
V圆柱=3.14×52×10≈0.785×103(mm3)
毛坯的体积V=3.74×103-0.785×103
≈2.96×103(mm3)=2.96(cm3)
约有毛坯:5.8×103÷(7.8×2.96)≈2.5×102(个)
答:这堆毛坯约有250个。2、用一张长12cm、宽8cm的铁皮围成圆柱形的侧面,该圆柱体积为 ______
(结果保留 )课堂练习1、已知一正四棱台的上底面边长为4cm,下底面边长为8cm,高为3cm,其体积为______112cm33、埃及胡夫金字塔大约建于公元前2580年,其形状为正四棱锥.金字塔高146.6米,底面边长230.4米.求这座金字塔的体积.V=2594046.0(m3)(2)柱、锥、台体积的计算公式及它们之间的联系(1)体积度量的基本思路:长方体体积公式是计算其他几何体体积的基础.问题6:回顾反思即特殊到一般的数学思想。RR球的体积:一个半径和高都等于R的圆柱,挖去一个
以上底面为底面,下底面圆心为顶点的圆锥
后,所得的几何体的体积与一个半径为R的
半球的体积相等。探究RRRS1探究球的表面积:球的表面积:设想一个球由许多顶点在球心,底面在球面上的“准锥体”组成,这些准锥体的底面并不是真的多边形,但只要其底面足够小,就可以把它们看成真正的锥体.1.一个正方体内接于半径为R的球内,求正方体的体积.2.一个平面截一个球得到直径是6cm的圆面,球心到这个平面的距离是4cm,求该球的表面积和体积.例: 如图是一个奖杯的三视图,单位是cm,
试画出它的直观图,并计算这个奖杯的体积.
(精确到0.01cm)86618515151111x/y/z/这个奖杯的体积为V=V正四棱台+V长方体+ V球
其中V正四棱台V正方体=6×8×18=864V球=所以这个奖杯的体积为V=1828.76cm3例2.已知一个正四面体内接一个表面积为36 的球内,求这个四面体的表面积和体积数学 因探索而精彩、 因应用而美丽!
