上海教育版五四学制数学:24.4(5)《相似三角形的判定》(参考资料)
文档属性
| 名称 | 上海教育版五四学制数学:24.4(5)《相似三角形的判定》(参考资料) |

|
|
| 格式 | rar | ||
| 文件大小 | 146.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-10 00:00:00 | ||
图片预览



文档简介
课件10张PPT。24.4(5)相似三角形的判定 关于三角形的判定方法
(1)定义法:对应角相等、对应边成比例
(2)预备定理:平行于三角形一边的直线和它两边(或两边延长线)相交,所构成的三角形和原三角形相似.
(3)判定定理1.两角对应相等两三角形相似
(4)判定定理2.两边对应成比例且夹角相等,两三角形相似
(5)判定定理3.三边对应成比例的两三角形相似
(6)直角三角形判定的方法
①以上各种判定方法均适用
②如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和直角对应成比例,那么这两个直角三角形相似
③直角三角形被斜边上的高分成的两个直角三角形和原三角形相似
?2.判定定理的适用范围
(1)已知有一角相等时,可选择判定定理1与判定定理2.
(2)有两边对应成比例时,可选择判定定理2与判定定理3.
(3)直角三角形判定先考虑判定直角三角形相似的方法.还可以考虑一般三角形相似的方法
说明:一般不用定义来判定三角形的相似.5、三角形相似的基本图形:
①平行型:如图1,“A”型即公共角对的边平行,“×”型即对顶角对的边平行,都可推出两个三角形相似;
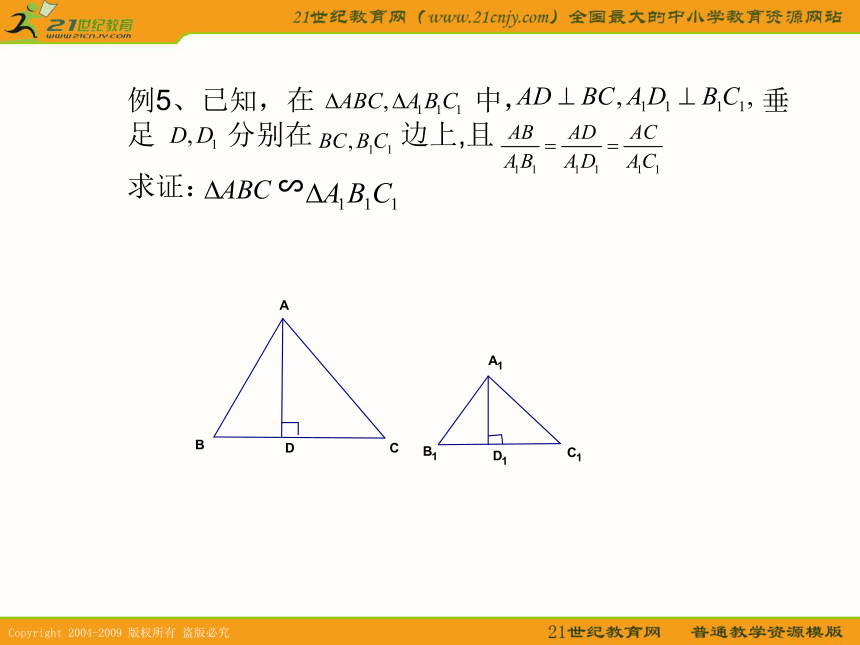
②相交线型:如图2,公共角对的边不平行,即相交或延长线相交或对顶角所对边延长相交.图中几种情况只要配上一对角相等,或夹公共角(或对顶角)的两边成比例,就可以判定两个三角形相似. 例5、已知,在 中, 垂足 分别在 边上,且
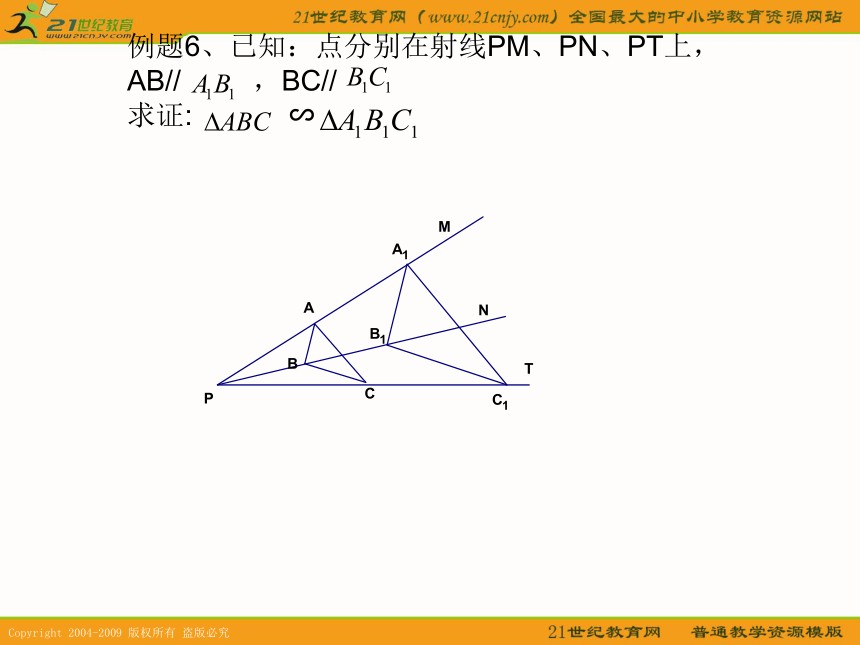
求证: ∽例题6、已知:点分别在射线PM、PN、PT上,AB// ,BC//
求证: ∽练习1:书后练习24.4(5)/1
练习2:书后练习24.4(5)/2
练习3、如图,在矩形ABCD中,E是CD的中点,BE⊥AC交AC于F,过F作FG∥AB交AE于G.
求证: =AF·FC.练习4、如图,在△ABC中,AD、BE分别是BC、AC上的高,AD、BE相交于H,则图中相似的三角形共有(??? )对A.3??????? B.4???? C.5??????? D.6练习5如图,D是△ABC一边BC上的一点,△ABC∽△DBA的条件是(??? )练习6 、已知过平行四边形ABCD的顶点C作一直线CF交BD于点E,交DA的延长线于点F,交AB于点M.
求证:课堂小结
1.关于三角形的判定方法
2.判定定理的适用范围
3.相似三角形与全等三角形判定方法的联系
4、相似三角形的判定定理的作用
5、三角形相似的基本图形
(1)定义法:对应角相等、对应边成比例
(2)预备定理:平行于三角形一边的直线和它两边(或两边延长线)相交,所构成的三角形和原三角形相似.
(3)判定定理1.两角对应相等两三角形相似
(4)判定定理2.两边对应成比例且夹角相等,两三角形相似
(5)判定定理3.三边对应成比例的两三角形相似
(6)直角三角形判定的方法
①以上各种判定方法均适用
②如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和直角对应成比例,那么这两个直角三角形相似
③直角三角形被斜边上的高分成的两个直角三角形和原三角形相似
?2.判定定理的适用范围
(1)已知有一角相等时,可选择判定定理1与判定定理2.
(2)有两边对应成比例时,可选择判定定理2与判定定理3.
(3)直角三角形判定先考虑判定直角三角形相似的方法.还可以考虑一般三角形相似的方法
说明:一般不用定义来判定三角形的相似.5、三角形相似的基本图形:
①平行型:如图1,“A”型即公共角对的边平行,“×”型即对顶角对的边平行,都可推出两个三角形相似;
②相交线型:如图2,公共角对的边不平行,即相交或延长线相交或对顶角所对边延长相交.图中几种情况只要配上一对角相等,或夹公共角(或对顶角)的两边成比例,就可以判定两个三角形相似. 例5、已知,在 中, 垂足 分别在 边上,且
求证: ∽例题6、已知:点分别在射线PM、PN、PT上,AB// ,BC//
求证: ∽练习1:书后练习24.4(5)/1
练习2:书后练习24.4(5)/2
练习3、如图,在矩形ABCD中,E是CD的中点,BE⊥AC交AC于F,过F作FG∥AB交AE于G.
求证: =AF·FC.练习4、如图,在△ABC中,AD、BE分别是BC、AC上的高,AD、BE相交于H,则图中相似的三角形共有(??? )对A.3??????? B.4???? C.5??????? D.6练习5如图,D是△ABC一边BC上的一点,△ABC∽△DBA的条件是(??? )练习6 、已知过平行四边形ABCD的顶点C作一直线CF交BD于点E,交DA的延长线于点F,交AB于点M.
求证:课堂小结
1.关于三角形的判定方法
2.判定定理的适用范围
3.相似三角形与全等三角形判定方法的联系
4、相似三角形的判定定理的作用
5、三角形相似的基本图形
