上海教育版五四学制数学:25.11《锐角三角比的意义》(参考资料)
文档属性
| 名称 | 上海教育版五四学制数学:25.11《锐角三角比的意义》(参考资料) |

|
|
| 格式 | rar | ||
| 文件大小 | 436.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-10 20:50:00 | ||
图片预览






文档简介
课件14张PPT。25.1(1)锐角三角比的意义九年级《数学》 小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1米.然后他很快就算出旗杆的高度了。你想知道小明怎样算出的吗? 情景引入(1)在Rt△ABC中,∠C=90o,∠A=30o,BC=35m,求CB . 1.观察(2) Rt△ABC,使∠C=90o,∠A=45o,计算∠A的对边与邻边比. 想一想 通过上面的计算,你能得到什么结论? 在一个直角三角形中,如果一个锐角等于30o,那么不管三角形的大小如何,这个角的对边与邻边的比值都等于;在一个直角三角形中,如果一个锐角等于45o,那么不管三角形的大小如何,这个角的对边与邻边的比值都等于1。 讨论 一般地,当∠A取其他一定度数的锐角时,它的对边与邻边的比是否也是一个定值?如图:Rt△ABC与Rt△A’B’C’,
∠C=∠DC’A =90°,∠A=α,
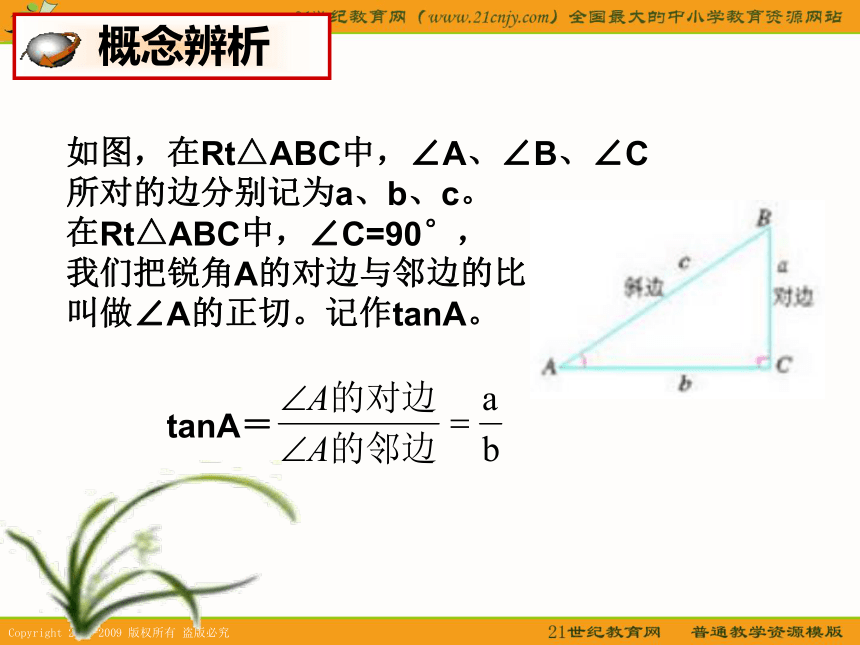
那么 与 有什么关系? 概念辨析结论:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值。 概念辨析如图,在Rt△ABC中,∠A、∠B、∠C
所对的边分别记为a、b、c。
在Rt△ABC中,∠C=90°,
我们把锐角A的对边与邻边的比
叫做∠A的正切。记作tanA。tanA= 概念辨析在Rt△ABC中,∠C=90°,我们把
锐角A的邻边与对边的比叫做∠A的
余切。记作cotA。cotA= 邻边/对边= 例题分析例题1. 在Rt⊿ABC中,∠C=900,
AC=3,BC=2,求tanA和tanB的值。解:在Rt⊿ABC中,
∵AC=3,BC=2
∴tanA= tanB= 例题分析例题2.在Rt⊿ABC中,∠C=900,
BC=4,AB=5,求cotA和cotB的值。
。.解:在Rt⊿ABC中,由勾股定理得
AB2=AC2+BC2
∵BC=4,AB=5,
∴AC=∴cotA= cotB=
问题拓展在上题中,在同一个直角三角形中,∠A的正切和余切有怎样的数量关系?∠B是∠A的余角,那么它们的正切、余切值之间有怎样的数量关系?. 在Rt⊿ABC中, ∠A+∠B=90°:
则有 tanA·cotA=1
tanA= tanB= 巩固练习1.如图,在直角△ABC中,∠C=90o,
若AB=5,AC=4,则cotA=_______.
2. 在△ABC中,∠C=90°,BC=2,tanA= ,则边AC的长是_________.3 小结. 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边(邻边与对边)的比是一个固定值。 作业练习册25.1(1)
∠C=∠DC’A =90°,∠A=α,
那么 与 有什么关系? 概念辨析结论:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值。 概念辨析如图,在Rt△ABC中,∠A、∠B、∠C
所对的边分别记为a、b、c。
在Rt△ABC中,∠C=90°,
我们把锐角A的对边与邻边的比
叫做∠A的正切。记作tanA。tanA= 概念辨析在Rt△ABC中,∠C=90°,我们把
锐角A的邻边与对边的比叫做∠A的
余切。记作cotA。cotA= 邻边/对边= 例题分析例题1. 在Rt⊿ABC中,∠C=900,
AC=3,BC=2,求tanA和tanB的值。解:在Rt⊿ABC中,
∵AC=3,BC=2
∴tanA= tanB= 例题分析例题2.在Rt⊿ABC中,∠C=900,
BC=4,AB=5,求cotA和cotB的值。
。.解:在Rt⊿ABC中,由勾股定理得
AB2=AC2+BC2
∵BC=4,AB=5,
∴AC=∴cotA= cotB=
问题拓展在上题中,在同一个直角三角形中,∠A的正切和余切有怎样的数量关系?∠B是∠A的余角,那么它们的正切、余切值之间有怎样的数量关系?. 在Rt⊿ABC中, ∠A+∠B=90°:
则有 tanA·cotA=1
tanA= tanB= 巩固练习1.如图,在直角△ABC中,∠C=90o,
若AB=5,AC=4,则cotA=_______.
2. 在△ABC中,∠C=90°,BC=2,tanA= ,则边AC的长是_________.3 小结. 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边(邻边与对边)的比是一个固定值。 作业练习册25.1(1)
