上海教育版五四学制数学:25.32《解直角三角形》(参考资料)
文档属性
| 名称 | 上海教育版五四学制数学:25.32《解直角三角形》(参考资料) |

|
|
| 格式 | rar | ||
| 文件大小 | 329.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-10 20:50:00 | ||
图片预览


文档简介
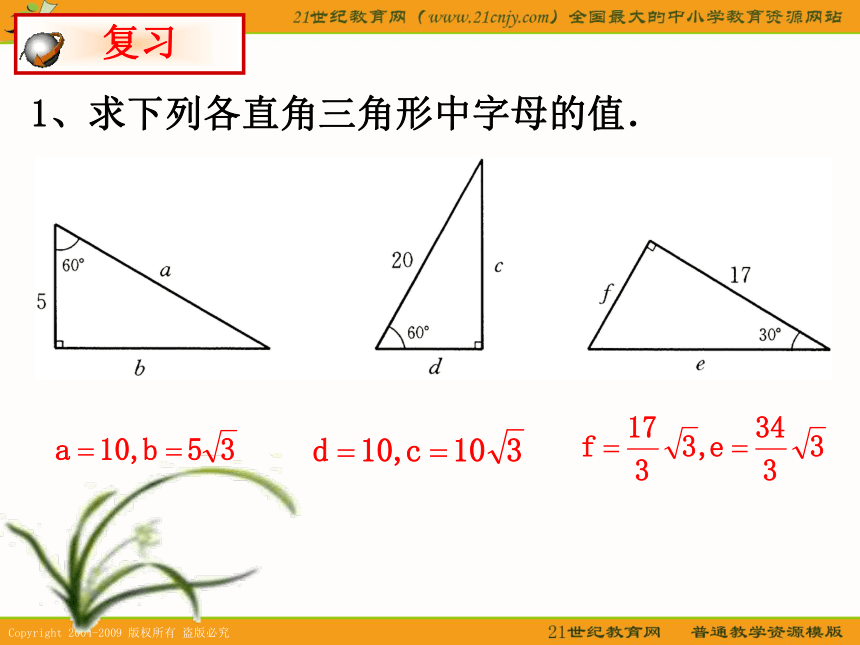
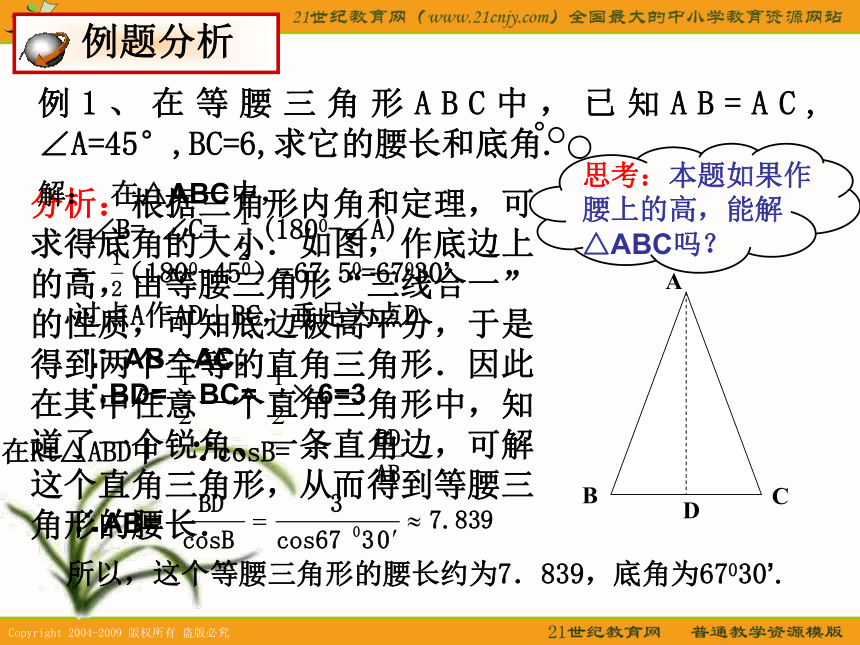
课件11张PPT。25.3(2) 解直角三角形九年级《数学》上海市青云中学 施秀宇 复习1、求下列各直角三角形中字母的值. 复习3、在△ABC中,∠C为直角,且b=20,B=35°,解这个三角形(精确到0.1).2、在△ABC中,∠C为直角,b= ,a= ,解这个三角形.∠A=55 °, a=28.6,c=34.9例1、在等腰三角形ABC中,已知AB=AC, ∠A=45°,BC=6,求它的腰长和底角. 例题分析 分析:根据三角形内角和定理,可求得底角的大小.如图,作底边上的高,由等腰三角形“三线合一”的性质,可知底边被高平分,于是得到两个全等的直角三角形.因此在其中任意一个直角三角形中,知道了一个锐角、一条直角边,可解这个直角三角形,从而得到等腰三角形的腰长. A CB
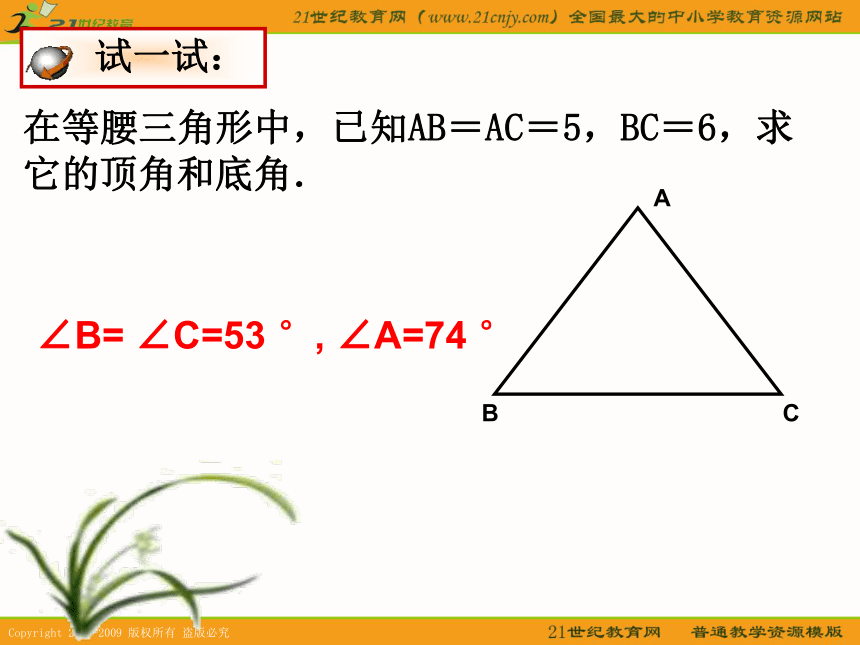
D解: 在△ABC中,过点A作AD⊥BC,垂足为点D∵ AB=AC,∴BD= BC= ×6=3 在Rt△ABD中 ∵cosB=∴AB=所以,这个等腰三角形的腰长约为7.839,底角为67030’.= (1800-450)=67.50=67030’∠B= ∠C= (1800-∠A)在等腰三角形中,已知AB=AC=5,BC=6,求它的顶角和底角. 试一试: ∠B= ∠C=53 °, ∠A=74 °例2、在△ABC中,AC=9,AB=8.5,∠A=38°,求AC边上的高及△ABC的面积.分析:分析:为了利用∠A的三角比,所以作出AC或AB边上的高,构造直角三角形,可求出一条高,再求出三角形的面积. 例题分析解:过点B作BD⊥AC,垂足为D.在Rt△ABD中 ∵sinA= ,∴ BD=AB·sinA=8.5×sin38°
≈5.233S△ABC= AC·BD= ×9×5.233≈23.55所以,AC边上的高约为5.233,△ABC的面积约为23.55.D 例题分析例3、如图,在⊿ABC中,∠A=30°,
tanB= ,AC=2,求AB. 分析:本题可以过点C作AB边的垂线,把∠A和∠B作在直角三角形中,再利用锐角三角比解决问题. DAB=1、课本24.3(2) 巩固练习 2、已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠B的四个三角比值.3、已知在直角梯形ABCD中,上底CD=4,下底AB=10,非直角腰BC= ,则底角∠B= ;sinB= ,cosB= ,tanB= ,cotB=60°4、如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.求:△ABC的面积(结果可保留根号).
巩固练习 课堂小结 2、本节课我们利用直角三角形的知识将某些一般三角形问题或梯形问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.今后,我们还要善于用数学知识解决实际问题. 1、今天你们学到了什么?有什么收获? 作业布置 练习册25.3(2)
D解: 在△ABC中,过点A作AD⊥BC,垂足为点D∵ AB=AC,∴BD= BC= ×6=3 在Rt△ABD中 ∵cosB=∴AB=所以,这个等腰三角形的腰长约为7.839,底角为67030’.= (1800-450)=67.50=67030’∠B= ∠C= (1800-∠A)在等腰三角形中,已知AB=AC=5,BC=6,求它的顶角和底角. 试一试: ∠B= ∠C=53 °, ∠A=74 °例2、在△ABC中,AC=9,AB=8.5,∠A=38°,求AC边上的高及△ABC的面积.分析:分析:为了利用∠A的三角比,所以作出AC或AB边上的高,构造直角三角形,可求出一条高,再求出三角形的面积. 例题分析解:过点B作BD⊥AC,垂足为D.在Rt△ABD中 ∵sinA= ,∴ BD=AB·sinA=8.5×sin38°
≈5.233S△ABC= AC·BD= ×9×5.233≈23.55所以,AC边上的高约为5.233,△ABC的面积约为23.55.D 例题分析例3、如图,在⊿ABC中,∠A=30°,
tanB= ,AC=2,求AB. 分析:本题可以过点C作AB边的垂线,把∠A和∠B作在直角三角形中,再利用锐角三角比解决问题. DAB=1、课本24.3(2) 巩固练习 2、已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠B的四个三角比值.3、已知在直角梯形ABCD中,上底CD=4,下底AB=10,非直角腰BC= ,则底角∠B= ;sinB= ,cosB= ,tanB= ,cotB=60°4、如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.求:△ABC的面积(结果可保留根号).
巩固练习 课堂小结 2、本节课我们利用直角三角形的知识将某些一般三角形问题或梯形问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.今后,我们还要善于用数学知识解决实际问题. 1、今天你们学到了什么?有什么收获? 作业布置 练习册25.3(2)
