南京市金陵中学高一数学同步辅导教材必修5一元二次不等式(P23-24)
文档属性
| 名称 | 南京市金陵中学高一数学同步辅导教材必修5一元二次不等式(P23-24) |

|
|
| 格式 | rar | ||
| 文件大小 | 100.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-11 09:42:00 | ||
图片预览

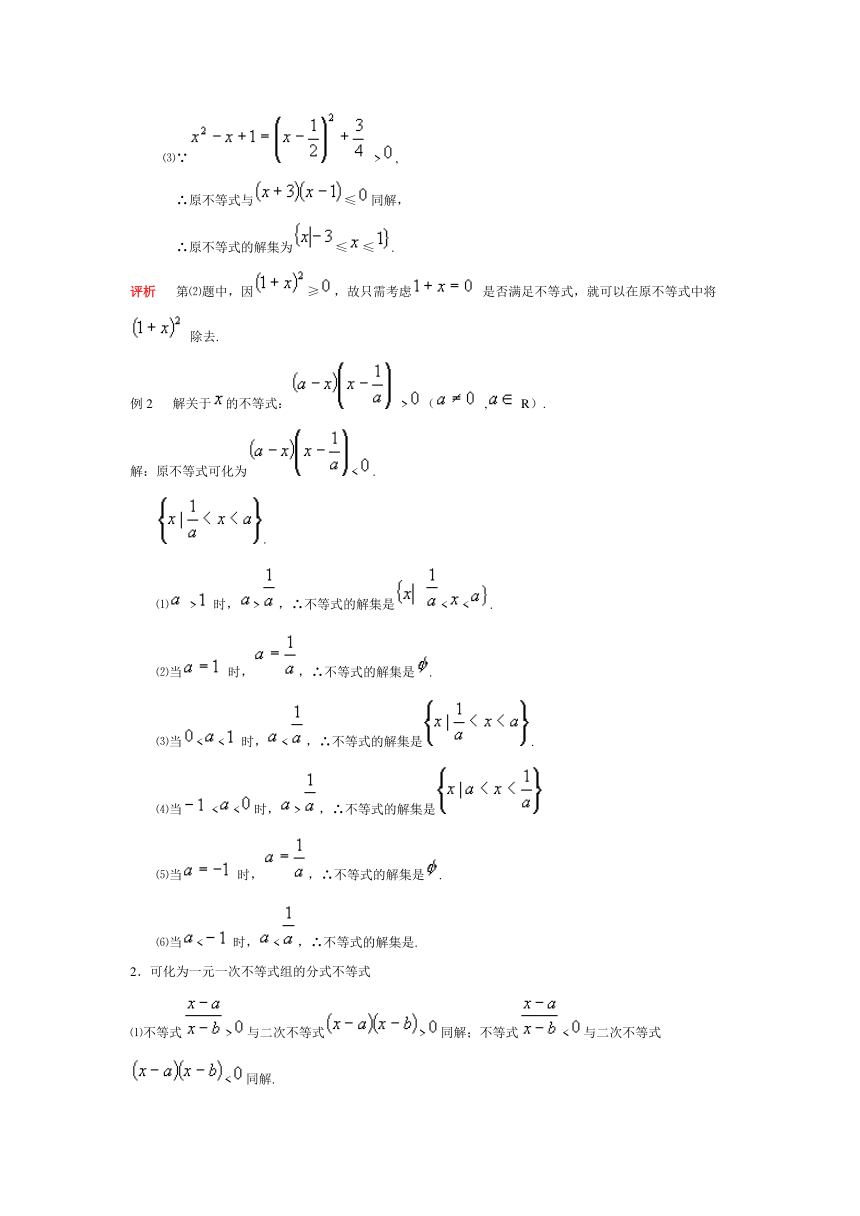



文档简介
南京市金陵中学高一数学同步辅导教材
一、本讲教学进度
1.5(P23-24)
二、本讲内容
1.一元二次不等式 >和 <的解法.
2.可化为一元一次不等式组的分式不等式.
3.二次函数在给定范围内的最值.
三、重点、难点选讲
1.一元二次不等式>和<的解法.
⑴因一元二次方程的两个根是,故有
一元二次不等式>,( < )的解集为 <,或 >.
一元二次不等式<,(<)的解集为 <<.
⑵引用上述结论时,必须注意不等式右边为零,两个括号中的系数为1的条件.
例1 解不等式:
⑴≤;
⑵ >;
⑶≤.
解:⑴原不等式即 ≤,
整理得 ≥,
≥.
∴不等式的解集为≤,或≥.
⑵∵≥,
∴由,得 不是原不等式的解.
当,得 >,
即 <, <<.
∴原不等式的解集为 <<,且.
⑶∵ >,
∴原不等式与≤同解,
∴原不等式的解集为≤≤.
评析 第⑵题中,因≥,故只需考虑 是否满足不等式,就可以在原不等式中将 除去.
例2 解关于的不等式: >( , R).
解:原不等式可化为<.
.
⑴ > 时,>,∴不等式的解集是 <<.
⑵当 时,,∴不等式的解集是.
⑶当<< 时,<,∴不等式的解集是.
⑷当 <<时,>,∴不等式的解集是
⑸当 时,,∴不等式的解集是.
⑹当< 时,<,∴不等式的解集是.
2.可化为一元一次不等式组的分式不等式
⑴不等式>与二次不等式>同解;不等式<与二次不等式<同解.
⑵不等式≥的解集是不等式>的解集与集合的并集;不等式≤的解集是不等式<的解集与集合的并集.
例3 解不等式:
⑴≥; ⑵≥.
解:(1)原不等式等价于≤.
∴不等式的解集是
=
(2)原不等式等价于.
∴不等式的解集是
评析:对带有等号的不等式求解,可以在相应的不含等号的不等式的解集中,增加使分子等于零的值,就得到所求解集.
例4:求不等式的解集.
解:不等式与不等式组 ① 等价.
, ②
由①, ,
∴
由②,,
∴.
∴原不等式的解集是
评析:(1)解 时,因不能确定的符号,所以不能把不等式两边同乘以而去分母,只能采用移项、通分的方法求解.
(2)本题也可以分两种情况考虑,①若>0,则-1< 恒成立,由 2,.②若<0,则 2恒成立.∵->0,∴将-1<两边同乘以-.得<-1,由①、②可得原不等式的解集是 < ,或≥.
例5 已知集合, ,且, .求实数a,b的值.
解:由已知,得 ,
.
由A ,从数轴可得集合B 又
和2是的实数根.
3. 二次函数在给定范围内的最值
由图像可以看出,二次函数当相应的抛物线开口向上时,在抛物线顶点处二次函数取得最小值,但无最大值;当抛物线开口向下时,在抛物线顶点处二次函数取得最大值,但无最小值.
如果将二次函数的自变量限制在某个范围内,则相应的图象仅是抛物线的一部分,这时函数可能既有最大值,又有最小值 例6 已知函数 ,
(1) 当 时,求的最大值、最小值 ;
(2) 当 时,求的最大值、最小值 ;
(3) 当 时,求的最大值、最小值 ;
解:函数即 ,抛物线的对称轴为直线 .
(1)当时,
由图象知,
当时,
当时,
(2)当时,
由图象知,
当时,
当时,
(3)当时,
由图象知,
当时,
当时,
评析 (1)此类问题通常根据题设条件画出函数的图象,并由图象求解.
(2)一般情况下,需要说明当x取什么值时, 函数取大或最小值.
例7 已知函数 求:
(1) 当时, 函数的最值;
(2) 当时, 函数的最值;
解:函数即 抛物线和对称轴为直线
(1) 当时,
由图象知,
当时,
函数无最大值.
(2) 当时,
由图象知,
当时,
函数无最大值.
评析 (1)最大值、最小值统称最值.
(2)根据题设条件画图象时,要注意表示x范围 的不等式中是否包含等号.当含等号时,相应的端点在图象上应画实圈;不含等号时,相应的端点不在图象上,应画空圈.
例8 求函数的最小值。
解:由题设,知令 则
由图象知,
当即时,
例9 关于的方程 有两个实根
(1) 求k的取值范围;
(2) 设 求 关于k的函数解析式,以及这个函数的最大值和最小值。
解:(1)由题意得
整理得
(2)由韦达定理,
∴
由图像可知,当 时,,
当 时,.
例10 已知函数,在内有最大值-5,求实数值.
解:函数变形为 .下面根据的不同情况进行讨论.
(1)当即时,由图(1)知,
当时, 取最大值
令得
(2) 当即时,由图(2)知,
当时, 取最大值
令
(3) 当 即时,由图(3)知,
当时, 取最大值
令(舍去),
∴由上知,或
评析 对分情况讨论的根据是与的关系。
练 习
; 一、 选择题
1.不等式的解集是( )
A.
C. D
2.不等式(x-4)(x+2)的解集是 ( )
A. B.
C. D
3. 不等式的解集是( )
A. B
C. D
4.不等式的解集是 ( )
A. B
C. D
5.当时,若函数的最大值为M,最小值为N,则( )
A.M=7,N=6 B.M=6,N=-2
C. M=7,N=-2 D.M=-6,N=-7
6.已知函数 则下列结论中不正确的是 ( )
A.当时, 有最大值3
B. 当时, 有最小值-15
C. 当时, 无最大值也无最小值
D. 当时,函数有最小值-5
二、填空题
7.不等式的解集是____________________________.
8.不等式的解集是____________________________.
9.设集合A= 则实数的取值范围是_____________.
10.10.当时,函数有最小值-2,则t= ______________.
三、解答题
11.解不等式:
12.设集合A=
若 实数a的取值范围。
13.关于x的不等式对一切x恒成立,求k的取值范围.
14.关于x的方程的两个实数 ,满足 求:
(1) 实数q关于p的函数表达式;
(2) 这个函数的最大值和最小值.
答案与提示
【答案】
一、 1.B 2.C 3.D 4.A 5.C 6.D
二、 7. 8.
9. 10.
三、11.解集为,或≥
12.≤≤
13.
14.⑴≤≤
⑵当, ;当,
【提示】
一、4.
5.,当, ;当,
6.
二、7.,,
8.≤,,且≤,解集是≤≤,且
9.,由数轴及 可知
10. ≤≤,抛物线的对称轴为直线.
⑴当≤≤时,的最小值 ∴.
⑵当,由图像知, 时, (不合). ∴
三、11.≥,≥,∴解集是,或≥
12.,,∴.
当.当,当.
由 知,≤≤.
13.原不等式即-.
∵,
∴原不等式等价于
不等式组
即 , ①
. ②
由①对 R恒成立,,,
.
由②对 R恒成立,,,.
∴的取值范围是.
14..
(1)由韦达定理,,
∵,∴,
.∵、为实根,∴≥,
即≥,≤2,≤≤,
∴ ≤≤.
(2)当 时, ;当 时,
一、本讲教学进度
1.5(P23-24)
二、本讲内容
1.一元二次不等式 >和 <的解法.
2.可化为一元一次不等式组的分式不等式.
3.二次函数在给定范围内的最值.
三、重点、难点选讲
1.一元二次不等式>和<的解法.
⑴因一元二次方程的两个根是,故有
一元二次不等式>,( < )的解集为 <,或 >.
一元二次不等式<,(<)的解集为 <<.
⑵引用上述结论时,必须注意不等式右边为零,两个括号中的系数为1的条件.
例1 解不等式:
⑴≤;
⑵ >;
⑶≤.
解:⑴原不等式即 ≤,
整理得 ≥,
≥.
∴不等式的解集为≤,或≥.
⑵∵≥,
∴由,得 不是原不等式的解.
当,得 >,
即 <, <<.
∴原不等式的解集为 <<,且.
⑶∵ >,
∴原不等式与≤同解,
∴原不等式的解集为≤≤.
评析 第⑵题中,因≥,故只需考虑 是否满足不等式,就可以在原不等式中将 除去.
例2 解关于的不等式: >( , R).
解:原不等式可化为<.
.
⑴ > 时,>,∴不等式的解集是 <<.
⑵当 时,,∴不等式的解集是.
⑶当<< 时,<,∴不等式的解集是.
⑷当 <<时,>,∴不等式的解集是
⑸当 时,,∴不等式的解集是.
⑹当< 时,<,∴不等式的解集是.
2.可化为一元一次不等式组的分式不等式
⑴不等式>与二次不等式>同解;不等式<与二次不等式<同解.
⑵不等式≥的解集是不等式>的解集与集合的并集;不等式≤的解集是不等式<的解集与集合的并集.
例3 解不等式:
⑴≥; ⑵≥.
解:(1)原不等式等价于≤.
∴不等式的解集是
=
(2)原不等式等价于.
∴不等式的解集是
评析:对带有等号的不等式求解,可以在相应的不含等号的不等式的解集中,增加使分子等于零的值,就得到所求解集.
例4:求不等式的解集.
解:不等式与不等式组 ① 等价.
, ②
由①, ,
∴
由②,,
∴.
∴原不等式的解集是
评析:(1)解 时,因不能确定的符号,所以不能把不等式两边同乘以而去分母,只能采用移项、通分的方法求解.
(2)本题也可以分两种情况考虑,①若>0,则-1< 恒成立,由 2,.②若<0,则 2恒成立.∵->0,∴将-1<两边同乘以-.得<-1,由①、②可得原不等式的解集是 < ,或≥.
例5 已知集合, ,且, .求实数a,b的值.
解:由已知,得 ,
.
由A ,从数轴可得集合B 又
和2是的实数根.
3. 二次函数在给定范围内的最值
由图像可以看出,二次函数当相应的抛物线开口向上时,在抛物线顶点处二次函数取得最小值,但无最大值;当抛物线开口向下时,在抛物线顶点处二次函数取得最大值,但无最小值.
如果将二次函数的自变量限制在某个范围内,则相应的图象仅是抛物线的一部分,这时函数可能既有最大值,又有最小值 例6 已知函数 ,
(1) 当 时,求的最大值、最小值 ;
(2) 当 时,求的最大值、最小值 ;
(3) 当 时,求的最大值、最小值 ;
解:函数即 ,抛物线的对称轴为直线 .
(1)当时,
由图象知,
当时,
当时,
(2)当时,
由图象知,
当时,
当时,
(3)当时,
由图象知,
当时,
当时,
评析 (1)此类问题通常根据题设条件画出函数的图象,并由图象求解.
(2)一般情况下,需要说明当x取什么值时, 函数取大或最小值.
例7 已知函数 求:
(1) 当时, 函数的最值;
(2) 当时, 函数的最值;
解:函数即 抛物线和对称轴为直线
(1) 当时,
由图象知,
当时,
函数无最大值.
(2) 当时,
由图象知,
当时,
函数无最大值.
评析 (1)最大值、最小值统称最值.
(2)根据题设条件画图象时,要注意表示x范围 的不等式中是否包含等号.当含等号时,相应的端点在图象上应画实圈;不含等号时,相应的端点不在图象上,应画空圈.
例8 求函数的最小值。
解:由题设,知令 则
由图象知,
当即时,
例9 关于的方程 有两个实根
(1) 求k的取值范围;
(2) 设 求 关于k的函数解析式,以及这个函数的最大值和最小值。
解:(1)由题意得
整理得
(2)由韦达定理,
∴
由图像可知,当 时,,
当 时,.
例10 已知函数,在内有最大值-5,求实数值.
解:函数变形为 .下面根据的不同情况进行讨论.
(1)当即时,由图(1)知,
当时, 取最大值
令得
(2) 当即时,由图(2)知,
当时, 取最大值
令
(3) 当 即时,由图(3)知,
当时, 取最大值
令(舍去),
∴由上知,或
评析 对分情况讨论的根据是与的关系。
练 习
; 一、 选择题
1.不等式的解集是( )
A.
C. D
2.不等式(x-4)(x+2)的解集是 ( )
A. B.
C. D
3. 不等式的解集是( )
A. B
C. D
4.不等式的解集是 ( )
A. B
C. D
5.当时,若函数的最大值为M,最小值为N,则( )
A.M=7,N=6 B.M=6,N=-2
C. M=7,N=-2 D.M=-6,N=-7
6.已知函数 则下列结论中不正确的是 ( )
A.当时, 有最大值3
B. 当时, 有最小值-15
C. 当时, 无最大值也无最小值
D. 当时,函数有最小值-5
二、填空题
7.不等式的解集是____________________________.
8.不等式的解集是____________________________.
9.设集合A= 则实数的取值范围是_____________.
10.10.当时,函数有最小值-2,则t= ______________.
三、解答题
11.解不等式:
12.设集合A=
若 实数a的取值范围。
13.关于x的不等式对一切x恒成立,求k的取值范围.
14.关于x的方程的两个实数 ,满足 求:
(1) 实数q关于p的函数表达式;
(2) 这个函数的最大值和最小值.
答案与提示
【答案】
一、 1.B 2.C 3.D 4.A 5.C 6.D
二、 7. 8.
9. 10.
三、11.解集为,或≥
12.≤≤
13.
14.⑴≤≤
⑵当, ;当,
【提示】
一、4.
5.,当, ;当,
6.
二、7.,,
8.≤,,且≤,解集是≤≤,且
9.,由数轴及 可知
10. ≤≤,抛物线的对称轴为直线.
⑴当≤≤时,的最小值 ∴.
⑵当,由图像知, 时, (不合). ∴
三、11.≥,≥,∴解集是,或≥
12.,,∴.
当.当,当.
由 知,≤≤.
13.原不等式即-.
∵,
∴原不等式等价于
不等式组
即 , ①
. ②
由①对 R恒成立,,,
.
由②对 R恒成立,,,.
∴的取值范围是.
14..
(1)由韦达定理,,
∵,∴,
.∵、为实根,∴≥,
即≥,≤2,≤≤,
∴ ≤≤.
(2)当 时, ;当 时,
