上海教育版五四学制数学:18.2正比例函数3(参考资料)
文档属性
| 名称 | 上海教育版五四学制数学:18.2正比例函数3(参考资料) |

|
|
| 格式 | rar | ||
| 文件大小 | 155.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-11 00:00:00 | ||
图片预览



文档简介
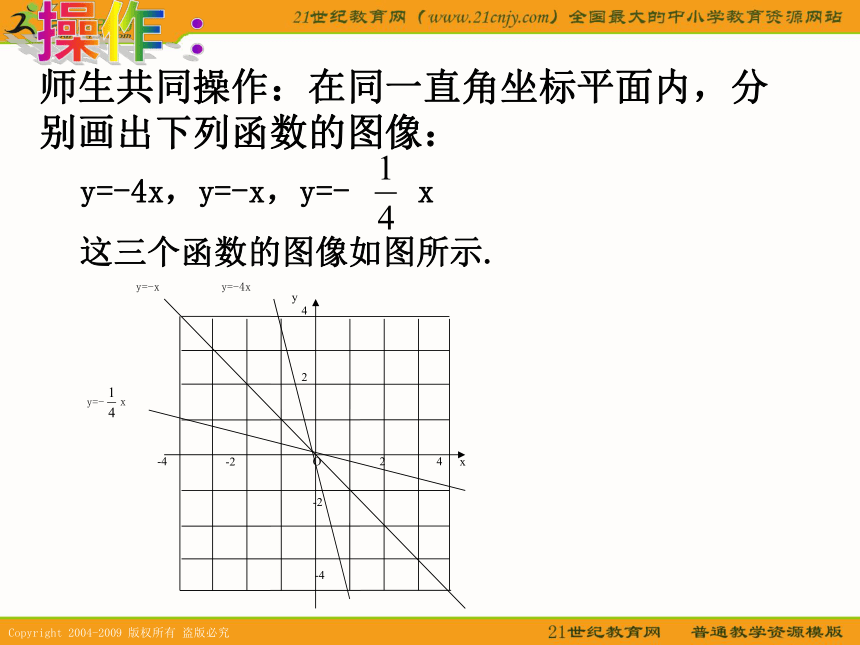
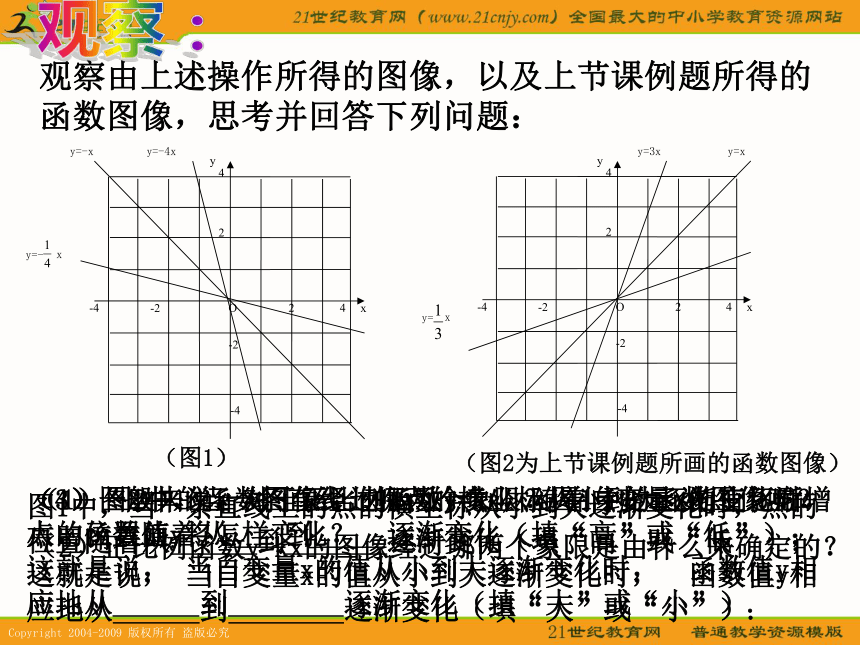
课件10张PPT。§18.2 正比例函数(3)操作:师生共同操作:在同一直角坐标平面内,分别画出下列函数的图像: y=-4x,y=-x,y=- x这三个函数的图像如图所示.观察由上述操作所得的图像,以及上节课例题所得的函数图像,思考并回答下列问题:(图2为上节课例题所画的函数图像)观察:
(图1)(1)图2中的函数图像经过哪两个象限?图1中的函数图像呢?(2)正比例函数y=kx的图像经过哪两个象限是由什么来确定的?(3)图2中,当一条直线上的点的横坐标从小到大逐渐变化时,点的位置随着从 到 逐渐变化(填“高”或“低”);
这就是说, 当自变量x的值从小到大逐渐变化时, 函数值y相应地从 到 逐渐变化(填“大”或“小”).图1中,当一条直线上的点的横坐标从小到大逐渐变化时,点的位置随着从 到 逐渐变化(填“高”或“低”);
这就是说, 当自变量x的值从小到大逐渐变化时, 函数值y相应地从 到 逐渐变化(填“大”或“小”).(4)一般来说,对于正比例函数y=kx,随着自变量x的值逐渐增大,函数值y将怎样变化?y=概括由画图的操作,通过观察和思考,讨论正比例函数有怎样的性质? 讨论正比例函数的性质:
(1)当k>0时,正比例函数的图像经过第一、三象限;自变量x的值逐渐增大时,y的值也随着逐渐增大.
(2)当k<0时,正比例函数的图像经过第二、四象限;自变量x的值逐渐增大时,y的值也随着逐渐减小.探索例题1:已知正比例函数y=(1-2a)x,如果y的值随x的值增大而减小,那么a的取值范围是什么?探索例题2:在水管放水的过程中,放水的时间x(分)与流出的水量y(立方米)是两个变量.已知水管每分钟流出的水量是0.2立方米,放水的过程持续10分钟,写出y与x之间的函数解析式,并指出函数的定义域,再画出这个函数的图像.解:在放水的过程中,变量y与x之间成正比例,比例系数是0.2,函数解析式是y=0.2x;函数的定义域是0≤x≤10.
这个函数的图像如图所示:
讨论在解决正比例函数实际应用问题时,应注意什么呢? 在实际问题中,两个变量y和x成正比例时,设x为自变量,比例系数为k,那么y是x的函数,这个函数的解析式是y=kx.但是,此时函数的定义域一般是部分实数,函数的图像一般就是直线的一部分(还可能只是在一条直线上的一些点).象这样的函数,我们对它进行研究时,可以把它看作正比例函数,但要特别注意它的定义域.你有什么收获?谈一谈电费y与用电总度数x成正比例.
已知当x=65(度),y=32.5(元).(2)求当x=26(度)时函数y的值.(1) 求正比例函数的解析式;练一练作业布置习题19.2(3)
(图1)(1)图2中的函数图像经过哪两个象限?图1中的函数图像呢?(2)正比例函数y=kx的图像经过哪两个象限是由什么来确定的?(3)图2中,当一条直线上的点的横坐标从小到大逐渐变化时,点的位置随着从 到 逐渐变化(填“高”或“低”);
这就是说, 当自变量x的值从小到大逐渐变化时, 函数值y相应地从 到 逐渐变化(填“大”或“小”).图1中,当一条直线上的点的横坐标从小到大逐渐变化时,点的位置随着从 到 逐渐变化(填“高”或“低”);
这就是说, 当自变量x的值从小到大逐渐变化时, 函数值y相应地从 到 逐渐变化(填“大”或“小”).(4)一般来说,对于正比例函数y=kx,随着自变量x的值逐渐增大,函数值y将怎样变化?y=概括由画图的操作,通过观察和思考,讨论正比例函数有怎样的性质? 讨论正比例函数的性质:
(1)当k>0时,正比例函数的图像经过第一、三象限;自变量x的值逐渐增大时,y的值也随着逐渐增大.
(2)当k<0时,正比例函数的图像经过第二、四象限;自变量x的值逐渐增大时,y的值也随着逐渐减小.探索例题1:已知正比例函数y=(1-2a)x,如果y的值随x的值增大而减小,那么a的取值范围是什么?探索例题2:在水管放水的过程中,放水的时间x(分)与流出的水量y(立方米)是两个变量.已知水管每分钟流出的水量是0.2立方米,放水的过程持续10分钟,写出y与x之间的函数解析式,并指出函数的定义域,再画出这个函数的图像.解:在放水的过程中,变量y与x之间成正比例,比例系数是0.2,函数解析式是y=0.2x;函数的定义域是0≤x≤10.
这个函数的图像如图所示:
讨论在解决正比例函数实际应用问题时,应注意什么呢? 在实际问题中,两个变量y和x成正比例时,设x为自变量,比例系数为k,那么y是x的函数,这个函数的解析式是y=kx.但是,此时函数的定义域一般是部分实数,函数的图像一般就是直线的一部分(还可能只是在一条直线上的一些点).象这样的函数,我们对它进行研究时,可以把它看作正比例函数,但要特别注意它的定义域.你有什么收获?谈一谈电费y与用电总度数x成正比例.
已知当x=65(度),y=32.5(元).(2)求当x=26(度)时函数y的值.(1) 求正比例函数的解析式;练一练作业布置习题19.2(3)
