上海教育版五四学制数学:24.3(2)《三角形一边的平行线》(参考资料)
文档属性
| 名称 | 上海教育版五四学制数学:24.3(2)《三角形一边的平行线》(参考资料) |

|
|
| 格式 | rar | ||
| 文件大小 | 203.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-11 12:34:00 | ||
图片预览




文档简介
课件17张PPT。24.3三角形一边的平行线 (2)一、复习1.提问:三角形一边的平行线的性质定理? 2.思考△ABC中,若DE∥BC,则 它们的值与
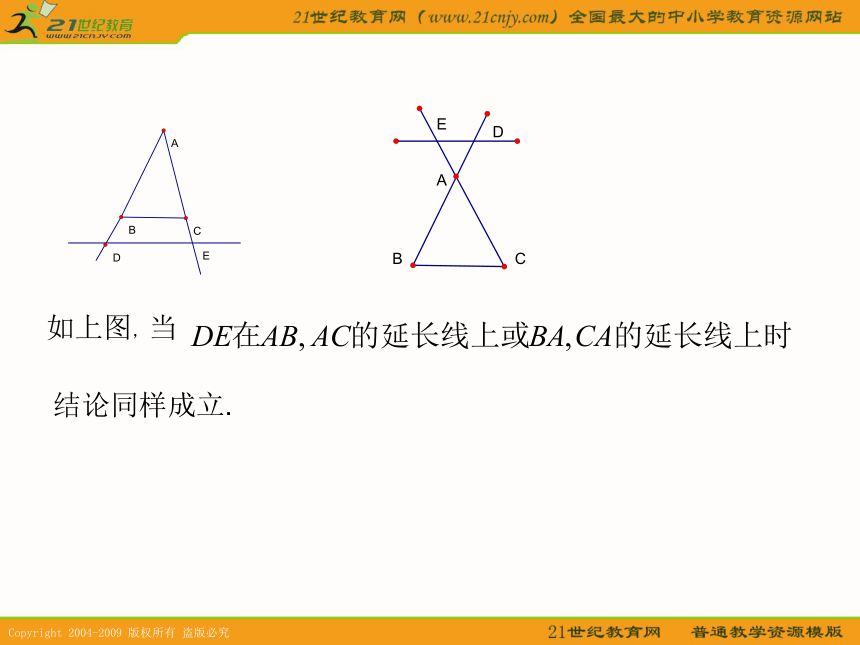
相等吗?为什么?二、学习新课 1.证明定理推论已知: ∥ 求证 证明:作 ∥ 交 于 ∥ 四边形DFCE为平行四边形,得FC=DE ∵ ∥ ∴ ∴ ∥ 得 ∴ 如上图,当结论同样成立.三角形一边的平行线性质定理推论:
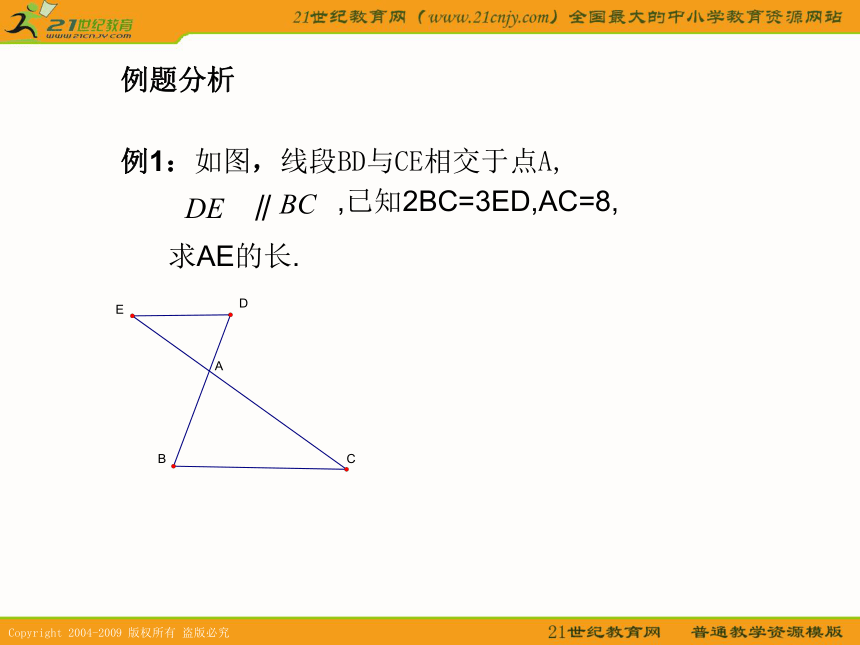
平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.例题分析 例1:如图,线段BD与CE相交于点A, ∥,已知2BC=3ED,AC=8,
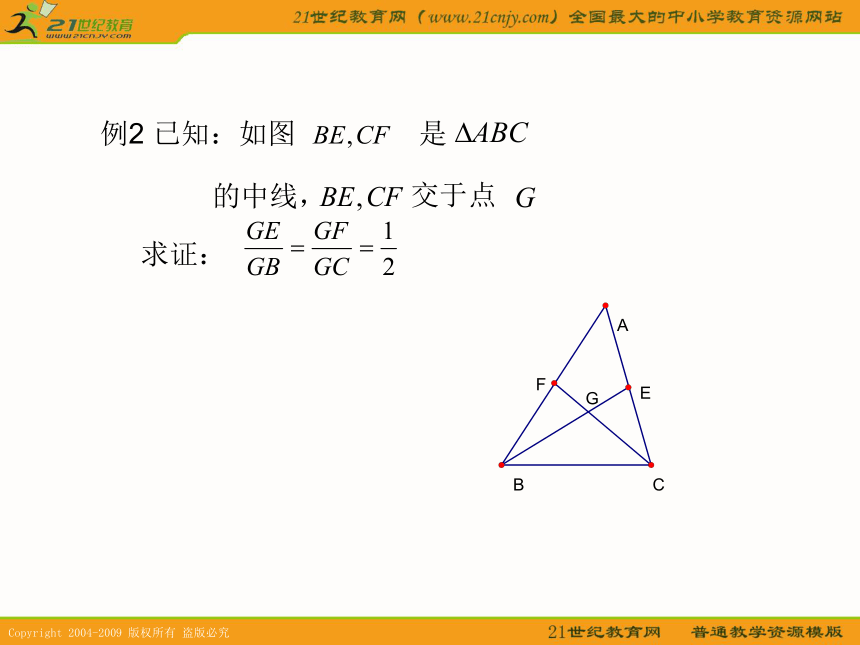
求AE的长.例2 已知:如图是求证: 的中线, 交于点重心的性质:三角形的重心到一
个顶点的距离,等于它到对边中点
的距离的两倍.例3:已知:在Rt中,∠,是中线交于点,求:例4:已知:在Rt 中,∠ ,
是重心, 于 ,
求 的长. 重心要掌握三要点: 1、定义:三角形三条中线相交于一点,这个 交点叫做三角形的重心.2、作法:两条中线的交点. 3 、性质:三角形的重心到一个顶点的距离,等于它到对边中点的距离的两倍.三、巩固练习 1.如图,在△ABC中,DE∥BC,AE=2,EC=3,DE=4,
求BC的长.2.如图:BD∥AC,CE=3,CD=5,AC=5,
求BD的长.3 :已知,△ABC中,∠C=90,G是三角形的重
心,AB=8.
求:① GC的长;
② 过点G的直线MN∥AB,交AC于M,BC
于N,求MN的长.4.已知,△ABC中,G是三角形的重心,AG⊥GC,AG=3,GC=4,求BG的长.四、课堂小结 1、今天学习的定理推论是:在原三角形中用平行线截出新三角形,可得这两个三角形的三对对应边成比例,特别注意与平行线分线段成比例定理的区别. 2、如果平行于三角形一边的直线,与三角形两边的延长线相交也可以用这个定理.3、重心的性质中到顶点的距离是到对边中点距离的两倍,不要混淆.五、作业布置 课本第15-16页,练习册
相等吗?为什么?二、学习新课 1.证明定理推论已知: ∥ 求证 证明:作 ∥ 交 于 ∥ 四边形DFCE为平行四边形,得FC=DE ∵ ∥ ∴ ∴ ∥ 得 ∴ 如上图,当结论同样成立.三角形一边的平行线性质定理推论:
平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.例题分析 例1:如图,线段BD与CE相交于点A, ∥,已知2BC=3ED,AC=8,
求AE的长.例2 已知:如图是求证: 的中线, 交于点重心的性质:三角形的重心到一
个顶点的距离,等于它到对边中点
的距离的两倍.例3:已知:在Rt中,∠,是中线交于点,求:例4:已知:在Rt 中,∠ ,
是重心, 于 ,
求 的长. 重心要掌握三要点: 1、定义:三角形三条中线相交于一点,这个 交点叫做三角形的重心.2、作法:两条中线的交点. 3 、性质:三角形的重心到一个顶点的距离,等于它到对边中点的距离的两倍.三、巩固练习 1.如图,在△ABC中,DE∥BC,AE=2,EC=3,DE=4,
求BC的长.2.如图:BD∥AC,CE=3,CD=5,AC=5,
求BD的长.3 :已知,△ABC中,∠C=90,G是三角形的重
心,AB=8.
求:① GC的长;
② 过点G的直线MN∥AB,交AC于M,BC
于N,求MN的长.4.已知,△ABC中,G是三角形的重心,AG⊥GC,AG=3,GC=4,求BG的长.四、课堂小结 1、今天学习的定理推论是:在原三角形中用平行线截出新三角形,可得这两个三角形的三对对应边成比例,特别注意与平行线分线段成比例定理的区别. 2、如果平行于三角形一边的直线,与三角形两边的延长线相交也可以用这个定理.3、重心的性质中到顶点的距离是到对边中点距离的两倍,不要混淆.五、作业布置 课本第15-16页,练习册
