上海教育版五四学制数学:24.31《三角形一边的平行线》(参考资料)
文档属性
| 名称 | 上海教育版五四学制数学:24.31《三角形一边的平行线》(参考资料) |

|
|
| 格式 | rar | ||
| 文件大小 | 178.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-11 12:33:00 | ||
图片预览



文档简介
课件14张PPT。24.3三角形一边的平行线 (1)一、复习
1、同底等高的三角形的面积比是多少?
2、等底不等高的三角形的面积比是多
少?
3、等高不等底的三角形的面积比是多少?
4若 则把这个乘积式化成比例式可以写成哪几种形式?
5、三角形的中位线有什么性质? 二、学习新课
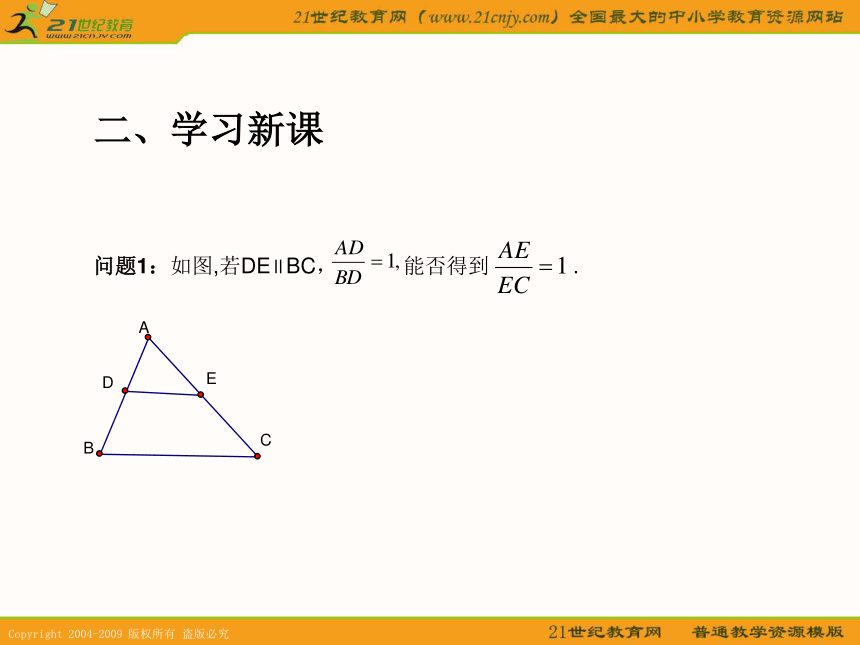
问题1:如图,若DE∥BC, 能否得到 .
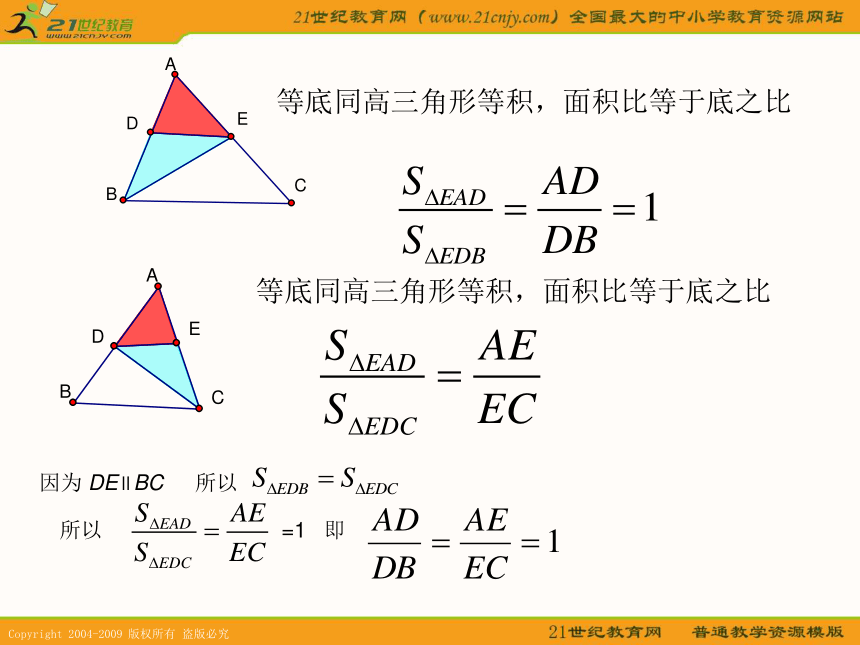
等底同高三角形等积,面积比等于底之比
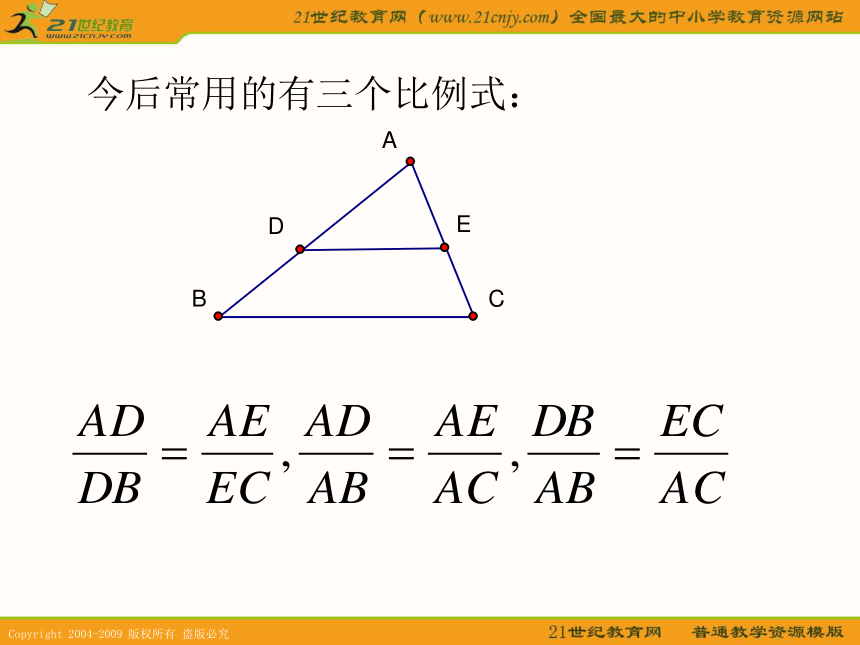
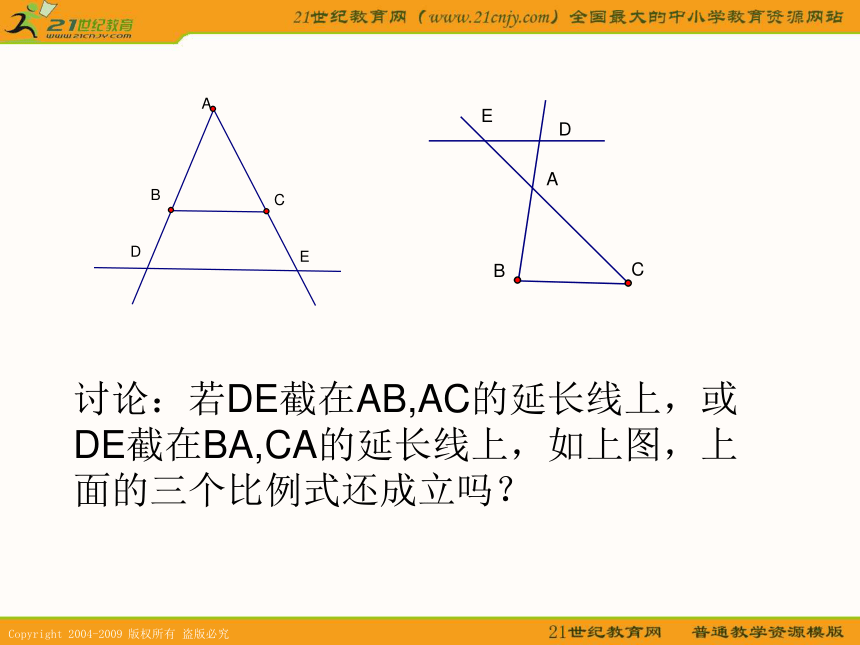
等底同高三角形等积,面积比等于底之比因为 DE∥BC所以 所以 =1 即问题2:若将 向下平行移动能否得到 ? 求证: 证明:联结EB,CD设 E到BA的距离为h ,则得同理可得 ∥议一议:利用比例的性质,还可以得到哪些成比例线段 已知: 直线 与边AB、AC分别相交于点D、E, 且∥ 今后常用的有三个比例式: 讨论:若DE截在AB,AC的延长线上,或DE截在BA,CA的延长线上,如上图,上面的三个比例式还成立吗?,三角形一边的平行线性质定理:平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.符号语言:∵DE∥BC
(或者)强调在同一条线段上的比例关系 2.例题分析 如图:已知
DE∥BC,AB=15,AC=10,BD=6.
求CE.解∵DE∥BC,∴ 由AB=15,AC=10,BD=6,得∴CE=4. X型 小结: “A”字型.三、巩固练习:1、在ABC中,DE∥BC,DE与AB相交于D,与AC相交于E.(1)已知, 求 的长.(2)已知 求 的长. (3)已知 3:2, 求 的长.2、 如图, 在⊿ABC中,DE∥BC, S ⊿BCD:S ⊿ABC=1:4,若AC=2,求EC的长.3、 如图,已知,AB∥CD∥EF,OA=14,AC=16,CE=8,BD=12,求OB、DF的长.4、如图, 在⊿ABC, DG∥EC, EG∥BC,求证: =AB· AD.四、课堂小结 1、这节课学习了哪个定理?你能叙述吗? 2、分别结合图形把所学的定理用符号语言叙述. 五、作业布置:书第13页,练习册
1、同底等高的三角形的面积比是多少?
2、等底不等高的三角形的面积比是多
少?
3、等高不等底的三角形的面积比是多少?
4若 则把这个乘积式化成比例式可以写成哪几种形式?
5、三角形的中位线有什么性质? 二、学习新课
问题1:如图,若DE∥BC, 能否得到 .
等底同高三角形等积,面积比等于底之比
等底同高三角形等积,面积比等于底之比因为 DE∥BC所以 所以 =1 即问题2:若将 向下平行移动能否得到 ? 求证: 证明:联结EB,CD设 E到BA的距离为h ,则得同理可得 ∥议一议:利用比例的性质,还可以得到哪些成比例线段 已知: 直线 与边AB、AC分别相交于点D、E, 且∥ 今后常用的有三个比例式: 讨论:若DE截在AB,AC的延长线上,或DE截在BA,CA的延长线上,如上图,上面的三个比例式还成立吗?,三角形一边的平行线性质定理:平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.符号语言:∵DE∥BC
(或者)强调在同一条线段上的比例关系 2.例题分析 如图:已知
DE∥BC,AB=15,AC=10,BD=6.
求CE.解∵DE∥BC,∴ 由AB=15,AC=10,BD=6,得∴CE=4. X型 小结: “A”字型.三、巩固练习:1、在ABC中,DE∥BC,DE与AB相交于D,与AC相交于E.(1)已知, 求 的长.(2)已知 求 的长. (3)已知 3:2, 求 的长.2、 如图, 在⊿ABC中,DE∥BC, S ⊿BCD:S ⊿ABC=1:4,若AC=2,求EC的长.3、 如图,已知,AB∥CD∥EF,OA=14,AC=16,CE=8,BD=12,求OB、DF的长.4、如图, 在⊿ABC, DG∥EC, EG∥BC,求证: =AB· AD.四、课堂小结 1、这节课学习了哪个定理?你能叙述吗? 2、分别结合图形把所学的定理用符号语言叙述. 五、作业布置:书第13页,练习册
