上海教育版五四学制数学:19.2(5)证明举例(5)(教学设计)
文档属性
| 名称 | 上海教育版五四学制数学:19.2(5)证明举例(5)(教学设计) |

|
|
| 格式 | rar | ||
| 文件大小 | 28.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-11 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
19.2(5)证明举例(5)
教学目标
1、通过证明举例的学习和实践,懂得演绎推理的一般规则,初步掌握规范的表达格式;了解证明之前进行分析的基本思路;
2、能利用全等三角形的判定与性质、等腰三角形的性质来证明有关线段相等、角相等的简单问题;
3、了解添置辅助线的基本方法,会添置常见的辅助线;
4、了解文字语言、图形语言、符号语言三种数学语言形态.
教学重点及难点
重点:分析基本思路,掌握规范的表达格式.
难点:辅助线的添加.21世纪教育网
教学用具准备[来源:21世纪教育网]
黑板、粉笔、学生准备课堂练习本.[来源:21世纪教育网]
教学流程设计
教学过程设计
1. 例题讲解
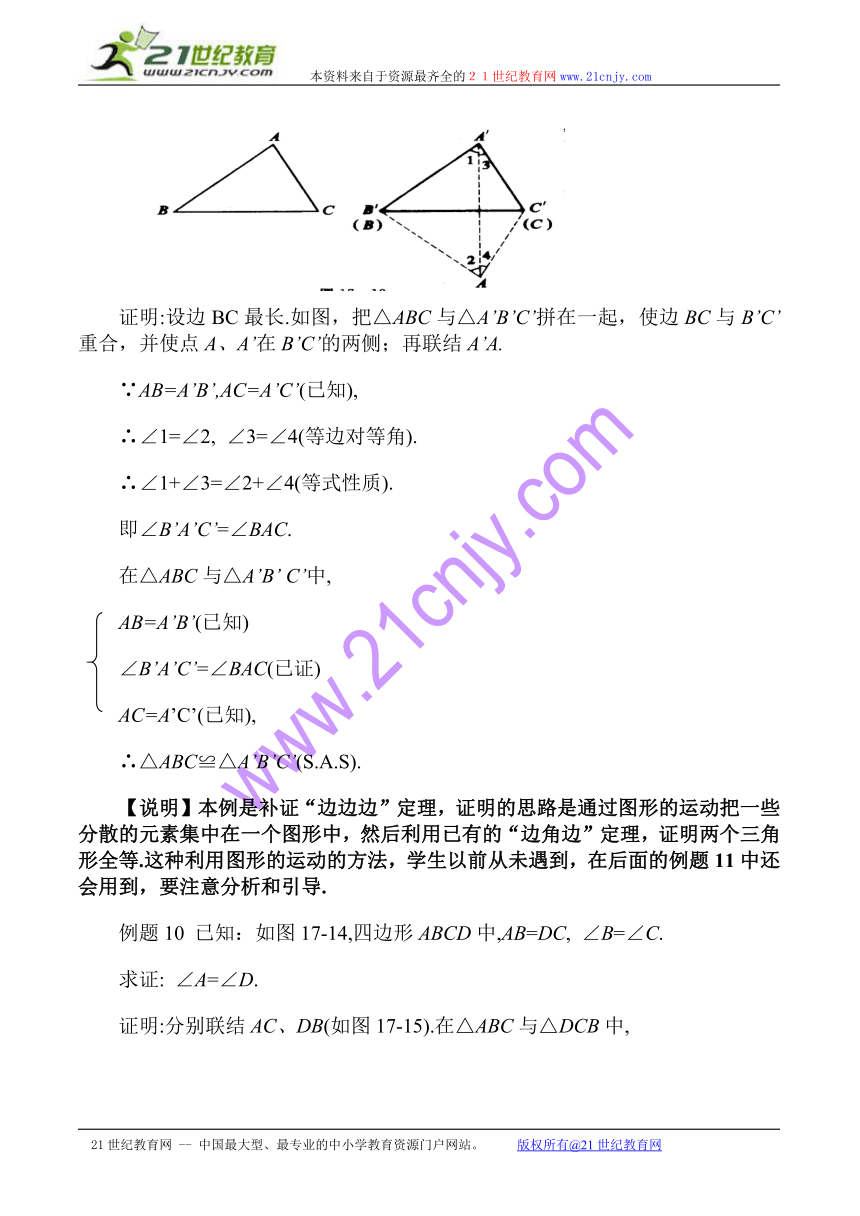
例题9 已知:如图,在△ABC与△A’B’C’中, AB=A’B’,BC= B’C’,CA=C’A’.
求证: △ABC≌△A’B’C’.
21世纪教育网
证明:设边BC最长.如图,把△ABC与△A’B’C’拼在一起,使边BC与B’C’重合,并使点A、A’在B’C’的两侧;再联结A’A.
∵AB=A’B’,AC=A’C’(已知),[来源:21世纪教育网]
∴∠1=∠2, ∠3=∠4(等边对等角).
∴∠1+∠3=∠2+∠4(等式性质).
即∠B’A’C’=∠BAC.
在△ABC与△A’B’ C’中,
AB=A’B’(已知)
∠B’A’C’=∠BAC(已证)21世纪教育网
AC=A’C’(已知),
∴△ABC≌△A’B’C’(S.A.S).
【说明】本例是补证“边边边”定理,证明的思路是通过图形的运动把一些分散的元素集中在一个图形中,然后利用已有的“边角边”定理,证明两个三角形全等.这种利用图形的运动的方法,学生以前从未遇到,在后面的例题11中还会用到,要注意分析和引导.
例题10 已知:如图17-14,四边形ABCD中,AB=DC, ∠B=∠C.[来源:21世纪教育网]
求证: ∠A=∠D.
证明:分别联结AC、DB(如图17-15).在△ABC与△DCB中,
AB=DC(已知)
∠ABC=∠DCB(已证)
BC=CB(已知),
∴△ABC≌△DCB(S.A.S)
得AC=DB(全等三角形的对应边相等).
在△ABD与△DCA中,
DB=AC(已知)
AB=DC(已知)
AD=DA(公共边),21世纪教育网21世纪教育网
∴△ABD≌△DCA(S.S.S)
∴∠BAD=∠CDA(全等三角形的对应角相等).
【说明】 本例是证明两个角相等,比较自然地会想到利用三角形全等.但通过分析,发现需要证两次三角形全等,有一定难度.对本例还介绍了通过构造等腰三角形来进行证明的第二种方法.两种方法都需要添加辅助线构造三角形,第一种方法的证明过程相对复杂些,但较第二种方法容易想到.21世纪教育网
怎样添置辅助线要在以后的学习中不断实践、探索、领悟,要重视图形的运动对添线的启示,而构造基本图形以及补全图形是常用的添线方法.
2.反馈练习,巩固知识
(1)已知:如图,AC与BD相交于点O,且AC=BD,AD=BC.
求证:OA=OB.
(2)已知:如图,点D、E在BC上,AB=AC,AD=AE.
求证:BD=CE.
3、课堂小结
你能讲一讲,证明角相等,一般可以采用什么方法吗?
4、布置作业
练习册.
例题讲解
巩固练习
回家作业
课堂小结
(第2题)
(第1题)
A
A
O
B
C
D
B
D
E
C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
19.2(5)证明举例(5)
教学目标
1、通过证明举例的学习和实践,懂得演绎推理的一般规则,初步掌握规范的表达格式;了解证明之前进行分析的基本思路;
2、能利用全等三角形的判定与性质、等腰三角形的性质来证明有关线段相等、角相等的简单问题;
3、了解添置辅助线的基本方法,会添置常见的辅助线;
4、了解文字语言、图形语言、符号语言三种数学语言形态.
教学重点及难点
重点:分析基本思路,掌握规范的表达格式.
难点:辅助线的添加.21世纪教育网
教学用具准备[来源:21世纪教育网]
黑板、粉笔、学生准备课堂练习本.[来源:21世纪教育网]
教学流程设计
教学过程设计
1. 例题讲解
例题9 已知:如图,在△ABC与△A’B’C’中, AB=A’B’,BC= B’C’,CA=C’A’.
求证: △ABC≌△A’B’C’.
21世纪教育网
证明:设边BC最长.如图,把△ABC与△A’B’C’拼在一起,使边BC与B’C’重合,并使点A、A’在B’C’的两侧;再联结A’A.
∵AB=A’B’,AC=A’C’(已知),[来源:21世纪教育网]
∴∠1=∠2, ∠3=∠4(等边对等角).
∴∠1+∠3=∠2+∠4(等式性质).
即∠B’A’C’=∠BAC.
在△ABC与△A’B’ C’中,
AB=A’B’(已知)
∠B’A’C’=∠BAC(已证)21世纪教育网
AC=A’C’(已知),
∴△ABC≌△A’B’C’(S.A.S).
【说明】本例是补证“边边边”定理,证明的思路是通过图形的运动把一些分散的元素集中在一个图形中,然后利用已有的“边角边”定理,证明两个三角形全等.这种利用图形的运动的方法,学生以前从未遇到,在后面的例题11中还会用到,要注意分析和引导.
例题10 已知:如图17-14,四边形ABCD中,AB=DC, ∠B=∠C.[来源:21世纪教育网]
求证: ∠A=∠D.
证明:分别联结AC、DB(如图17-15).在△ABC与△DCB中,
AB=DC(已知)
∠ABC=∠DCB(已证)
BC=CB(已知),
∴△ABC≌△DCB(S.A.S)
得AC=DB(全等三角形的对应边相等).
在△ABD与△DCA中,
DB=AC(已知)
AB=DC(已知)
AD=DA(公共边),21世纪教育网21世纪教育网
∴△ABD≌△DCA(S.S.S)
∴∠BAD=∠CDA(全等三角形的对应角相等).
【说明】 本例是证明两个角相等,比较自然地会想到利用三角形全等.但通过分析,发现需要证两次三角形全等,有一定难度.对本例还介绍了通过构造等腰三角形来进行证明的第二种方法.两种方法都需要添加辅助线构造三角形,第一种方法的证明过程相对复杂些,但较第二种方法容易想到.21世纪教育网
怎样添置辅助线要在以后的学习中不断实践、探索、领悟,要重视图形的运动对添线的启示,而构造基本图形以及补全图形是常用的添线方法.
2.反馈练习,巩固知识
(1)已知:如图,AC与BD相交于点O,且AC=BD,AD=BC.
求证:OA=OB.
(2)已知:如图,点D、E在BC上,AB=AC,AD=AE.
求证:BD=CE.
3、课堂小结
你能讲一讲,证明角相等,一般可以采用什么方法吗?
4、布置作业
练习册.
例题讲解
巩固练习
回家作业
课堂小结
(第2题)
(第1题)
A
A
O
B
C
D
B
D
E
C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
