等腰梯形的性质

等腰梯形的性质课时教案
授课教师：南苑中学 刘淑艳
课 题 16.8等腰梯形的性质
教材版本 北京市义务教育课程改革试验教材
教学目标 1、掌握等腰梯形的性质定理并能进行简单的应用。2、经历探索等腰梯形性质的过程，初步掌握等腰梯形的辅助线的添加方法，进一步体会化未知为已知的转化思想。3、在数学活动中感受数学证明的严谨性。
教学重点 等腰梯形性质定理的证明及简单应用
教学难点 正确添加辅助线解决等腰梯形问题
教学用具 多媒体 自制等腰梯形教具
教学过程
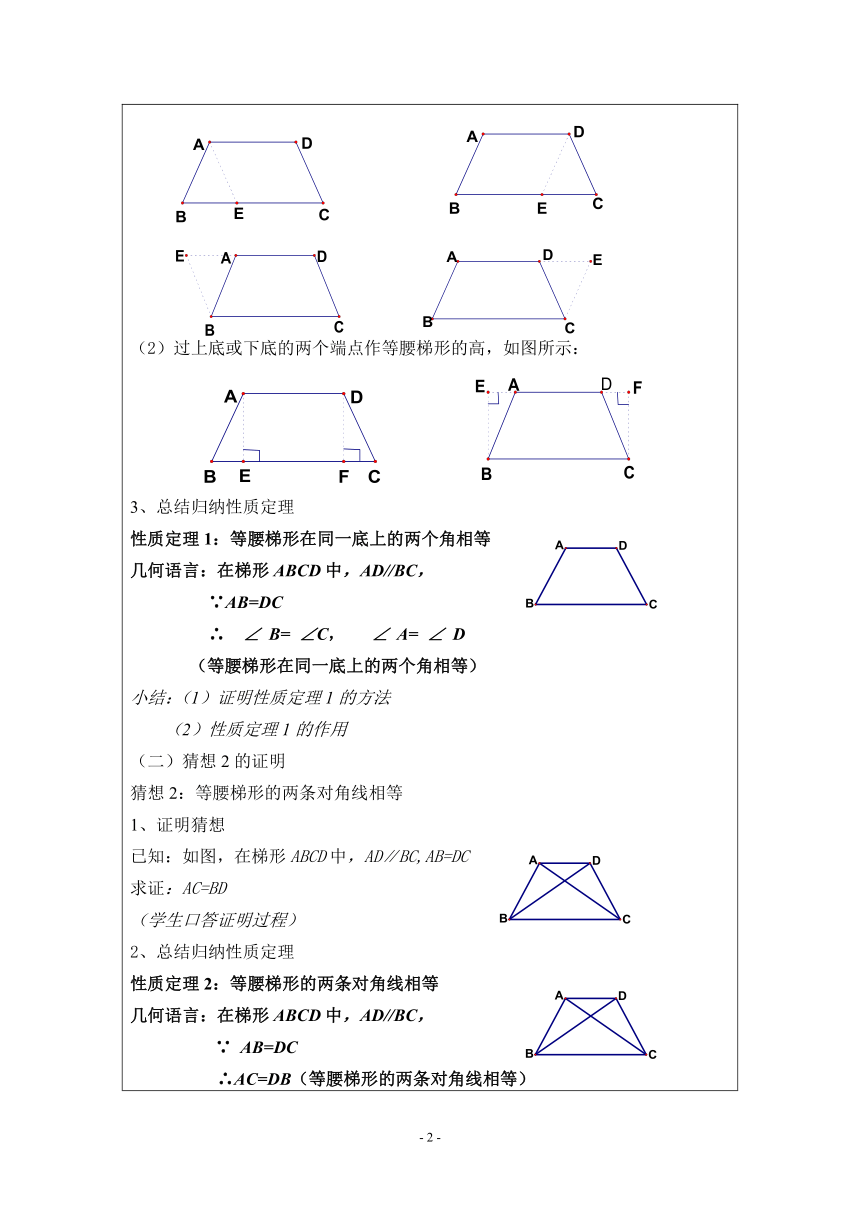
一、复习旧知 引入新课（一）回忆：1、梯形的有关概念。2、等腰梯形的对称性。（二）观察猜想（教师演示等腰梯形的轴对称性，学生观察猜想）猜想1：等腰梯形在同一底上的两个角相等二、 证明猜想 得出新知（一）合作探究证明猜想11、证明猜想（小组合作完成）猜想1：等腰梯形在同一底上的两个角相等已知：如图，在梯形ABCD中，AD∥BC,AB=DC求证：∠B=∠C，分析：证明两角相等通常采用的方法。 2、证明方法总结(1)过等腰梯形的顶点作腰的平行线，将等腰梯形转化为一个平行四边形和一个等腰三角形。如图所示: （2）过上底或下底的两个端点作等腰梯形的高，如图所示：3、总结归纳性质定理性质定理1：等腰梯形在同一底上的两个角相等几何语言：在梯形ABCD中，AD//BC， ∵AB=DC ∴ ∠ B= ∠C， ∠ A= ∠ D（等腰梯形在同一底上的两个角相等）小结：（1）证明性质定理1的方法（2）性质定理1的作用（二）猜想2的证明猜想2：等腰梯形的两条对角线相等1、证明猜想已知：如图，在梯形ABCD中，AD∥BC,AB=DC 求证：AC=BD（学生口答证明过程）2、总结归纳性质定理性质定理2：等腰梯形的两条对角线相等几何语言：在梯形ABCD中，AD//BC，∵ AB=DC ∴AC=DB（等腰梯形的两条对角线相等）3、小结：等腰梯形的性质 （1）等腰梯形在同一底上的两个角相等（2）等腰梯形的两条对角线相等三、应用新知 巩固练习（一）例题分析例：已知：如图，在等腰梯形ABCD中，AD∥BC，AB=CD,∠B=60° ，AD=4,BC=6，求：腰CD的长（学生独立完成并板演）方法一： 过点A作AE∥DC交BC于E 方法二：分别过点A、D作AE⊥BC, DF⊥BC,垂足分别为E、F(二)课堂练习1、在等腰梯形ABCD中，AD∥BC,AB=CD AD＝3cm,AB＝4cm,∠B＝60°, 则下底BC的长为 cm2、在等腰梯形ABCD中,AD∥BC,AB=DC,AD=2,BC=4,高DF=2,则腰长___3、已知：如图，在等腰梯形ABCD中,AD∥BC,AB=DC，△DBC沿BC翻折得到△EBC，问：四边形ABEC为什么四边形 总结归纳 课堂小结今天你学到了什么？还有什么问题？（一）知识方面1、等腰梯形在同一底上的两个角相等2、等腰梯形的两条对角线相等（二）学习方法1、研究等腰梯形的问题时常添加辅助线的方法（1）平移一腰构成一个等腰三角形和一个平行四边形（2）过上底的端点作下底的垂线或过下底的端点作上底延长线的垂线构成两个全等的直角三角形和一个矩形2、一种研究新问题常用的方法——将未知的问题转化为已知的转化的数学方法五、作业：三级跳97页5题 书98页练习1、2、3六、板书设计：
16.8等腰梯形的性质
性质定理1： 例题：
性质定理2：
- 3 -