新课标A版必修1第一章集合与函数概念13函数基本性质同步学案
文档属性
| 名称 | 新课标A版必修1第一章集合与函数概念13函数基本性质同步学案 |

|
|
| 格式 | rar | ||
| 文件大小 | 54.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-14 00:00:00 | ||
图片预览

文档简介
【本讲教育信息】
一. 教学内容:
函数基本性质
二. 重点、难点:
1. 函数单调性及单调区间的定义
2. 定义法证明函数单调性
3. 函数单调区间分析
4. 最大值与最小值的求法
5. 奇偶性的判断与证明
6. 单调性、奇偶性综合应用
【典型例题】
[例1] 用定义证明下列函数的单调性
(1)为R上减函数
(2)为()上增函数
解:
(1)任取
∴
∴ 为R上减函数
(2)任取
∵ ∴
∵
∴ ∴
∴ 在()上为增函数
[例2] 求下列函数单调递增区间
(1)
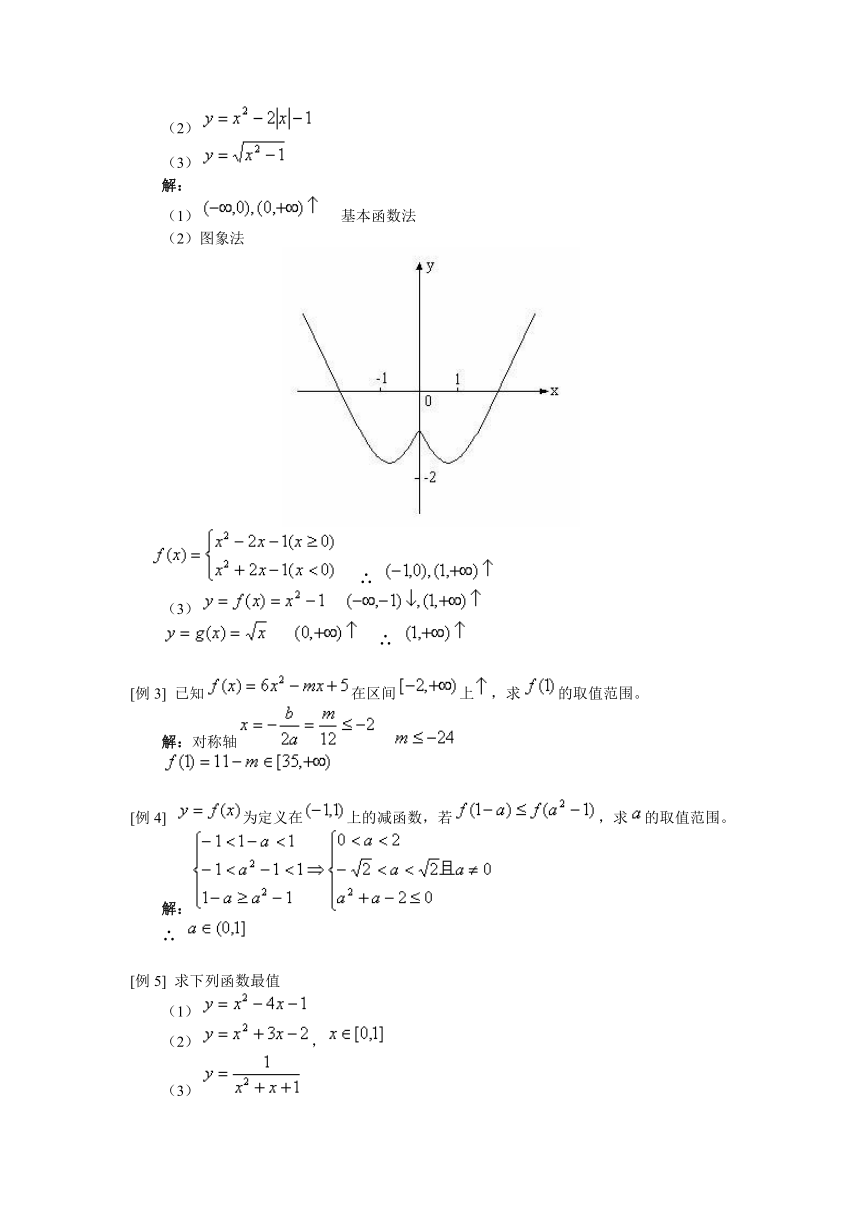
(2)
(3)
解:
(1) 基本函数法
(2)图象法
∴
(3)
∴
[例3] 已知在区间上,求的取值范围。
解:对称轴
[例4] 为定义在上的减函数,若,求的取值范围。
解:
∴
[例5] 求下列函数最值
(1)
(2),
(3)
解:
(1)
(2)
(3)
[例6] 判断下列函数奇偶性
(1)
(2)
(3)
(4)
(5)
(6)
解:
(1)不对称,非奇非偶
(2),奇函数
(3),偶函数
(4)既奇又偶
(5)
奇函数
(6)
时,
时,
∴ 奇函数
[例7] 求下列函数解析式
(1)奇函数,偶函数,且,求解析式;
(2)R上偶函数,时,,求解析式;
(3)R上奇函数,时,,求解析式。
解:
(1)
∴
(2)时,
∴
(3) ∴
时,
∴
[例8] 求参数的值
(1)为R上偶函数,求;
(2)为R奇函数,求。
解:
(1)
(2)检验正确
【模拟试题】
1. 为R上奇函数,为R上偶函数,在与图象重合,均为增函数,已知,下列不等式中正确的序号为 。
(1)
(2)
(3)
(4)
2. ,,则 。
3. 对一切实数,有,求证:为奇函数。
4. ,,对一切有,求证:为偶函数。
5. 为R上偶函数,为R上奇函数,判断下列函数奇偶性
(1)
(2)
(3)
(4)
(5)
(6)
【试题答案】
1.(1)(3)
2. ∴
3. 令 ∴
令 ∴ ∴ 奇函数
4. 令
∴
令 ∴
令 ∴ ∴ 偶函数
5.
(1)(2)不确定
(3)(4)奇函数
(5)(6)偶函数
一. 教学内容:
函数基本性质
二. 重点、难点:
1. 函数单调性及单调区间的定义
2. 定义法证明函数单调性
3. 函数单调区间分析
4. 最大值与最小值的求法
5. 奇偶性的判断与证明
6. 单调性、奇偶性综合应用
【典型例题】
[例1] 用定义证明下列函数的单调性
(1)为R上减函数
(2)为()上增函数
解:
(1)任取
∴
∴ 为R上减函数
(2)任取
∵ ∴
∵
∴ ∴
∴ 在()上为增函数
[例2] 求下列函数单调递增区间
(1)
(2)
(3)
解:
(1) 基本函数法
(2)图象法
∴
(3)
∴
[例3] 已知在区间上,求的取值范围。
解:对称轴
[例4] 为定义在上的减函数,若,求的取值范围。
解:
∴
[例5] 求下列函数最值
(1)
(2),
(3)
解:
(1)
(2)
(3)
[例6] 判断下列函数奇偶性
(1)
(2)
(3)
(4)
(5)
(6)
解:
(1)不对称,非奇非偶
(2),奇函数
(3),偶函数
(4)既奇又偶
(5)
奇函数
(6)
时,
时,
∴ 奇函数
[例7] 求下列函数解析式
(1)奇函数,偶函数,且,求解析式;
(2)R上偶函数,时,,求解析式;
(3)R上奇函数,时,,求解析式。
解:
(1)
∴
(2)时,
∴
(3) ∴
时,
∴
[例8] 求参数的值
(1)为R上偶函数,求;
(2)为R奇函数,求。
解:
(1)
(2)检验正确
【模拟试题】
1. 为R上奇函数,为R上偶函数,在与图象重合,均为增函数,已知,下列不等式中正确的序号为 。
(1)
(2)
(3)
(4)
2. ,,则 。
3. 对一切实数,有,求证:为奇函数。
4. ,,对一切有,求证:为偶函数。
5. 为R上偶函数,为R上奇函数,判断下列函数奇偶性
(1)
(2)
(3)
(4)
(5)
(6)
【试题答案】
1.(1)(3)
2. ∴
3. 令 ∴
令 ∴ ∴ 奇函数
4. 令
∴
令 ∴
令 ∴ ∴ 偶函数
5.
(1)(2)不确定
(3)(4)奇函数
(5)(6)偶函数
