初二下学期期末试题(青岛版)
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
初二下学期期末试题(青岛版)
一、选择题(36分)
1、下面计算正确的是( )
A.;B.;C.;D.
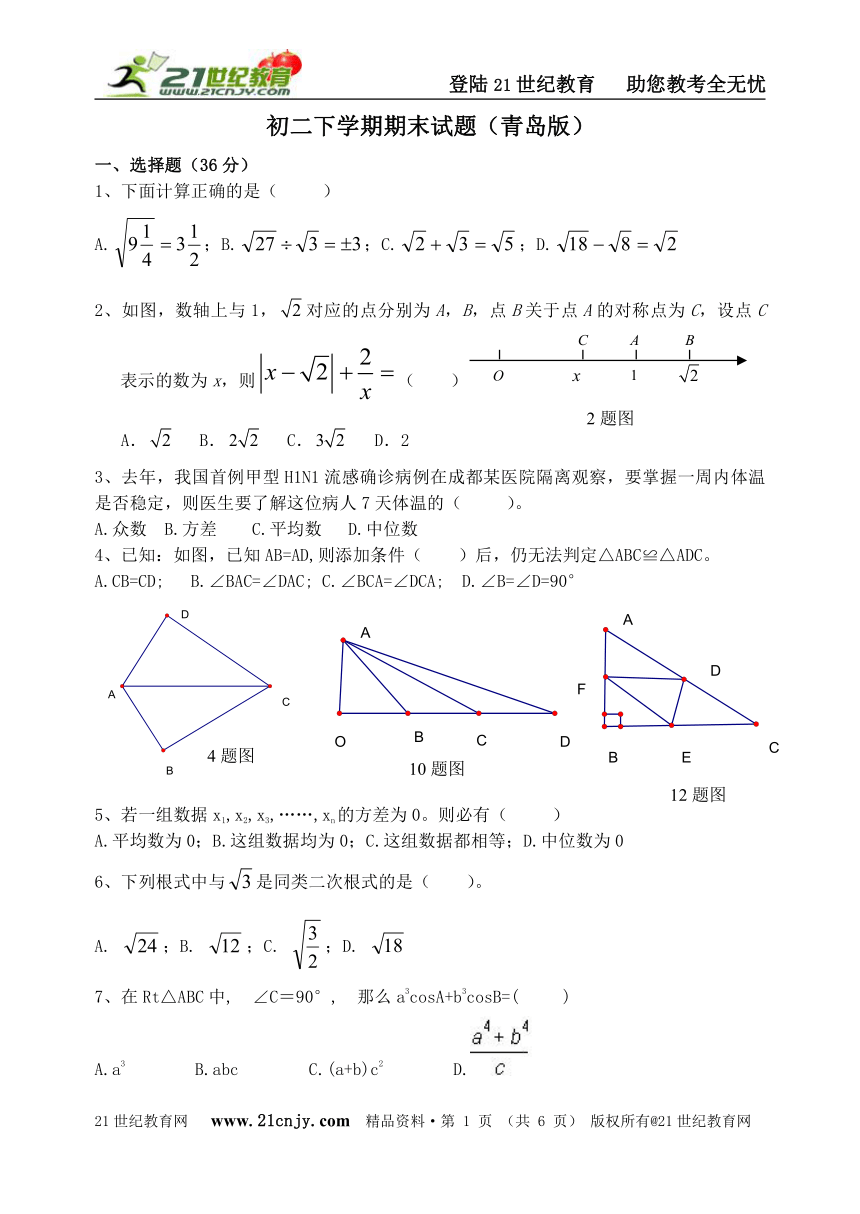
2、如图,数轴上与1,对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则( )
A. B. C. D.2
3、去年,我国首例甲型H1N1流感确诊病例在成都某医院隔离观察,要掌握一周内体温是否稳定,则医生要了解这位病人7天体温的( )。
A.众数 B.方差 C.平均数 D.中位数
4、已知:如图,已知AB=AD,则添加条件( )后,仍无法判定△ABC≌△ADC。
A.CB=CD; B.∠BAC=∠DAC; C.∠BCA=∠DCA; D.∠B=∠D=90°
5、若一组数据x1,x2,x3,……,xn的方差为0。则必有( )
A.平均数为0;B.这组数据均为0;C.这组数据都相等;D.中位数为0
6、下列根式中与是同类二次根式的是( )。
A. ;B. ;C. ;D.
7、在Rt△ABC中, ∠C=90°, 那么a3cosA+b3cosB=( )
A.a3 B.abc C.(a+b)c2 D.
8、一条斜坡公路坡度为i=1:3,这段公路长100米,则坡底到坡顶这段公路升高( )米。
A.30;B.10;C.;D.。
9、△ABC中,P为AB上一点,下列四个条件:(1)∠ACP=∠B;(2)∠APC=∠ACB;(3)AC2=AP×AB;(4).只添加其中一个条件,能使△APC∽△ACB的条件可以是( )。A.(1)(2)(4);B.(1)(3)(4);C.(2)(3)(4);D.(1)(2)(3)。
10、如图,已知:∠AOD=90°,OA=OB=BC=CD,则下列结论成立的是( )
A.△OAB∽△OCA;B.△OAB∽△ODA;C.△ABC∽△ACD;D.△ABC∽△DBA
11、下列命题:(1)如果a2=b2,那么a=b;(2)如果△ABC的三边满足:a2+b2=c2,那么∠C=90°;(3)如果,那么a、b互为相反数;(4)如果两个直角三角形全等,那么这两个直角三角形有两边对应相等。逆命题正确的有( )个。
A.1;B.2;C.3;D.4
12、Rt△ABC中,∠B=90°,AB=6,BC=8。将△ABC沿DE折叠,使C落在AB边F处,且DF∥BC,则CD=( )
二、填空题(20分)
13、代数式则P(m,n)在直角坐标系的第________象限。
14、等腰三角形两边长为4cm,6cm.则底角的余弦值为_____________.
15、一直角三角形两边为,则第三边为____________.
16、将一副三角板如图叠放,∠D=30°,∠A=45°,则△AOB与△DOC的面积比为______.
17、用反证法证明:在三角形中至少有一个内角小于或等于60°时,第一步
应假设:________________________________________________。
三、解答题(64分)
18、(8分)计算:
19、(8分)已知:如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,PC=4。求:PD的长。
20、(8分)
21、(8分)在Rt△ABC中,∠ACB=90°,BC=3,AC=4。AB的垂直平分线DE交BC的延长线于点E,求CE的长。
22、(8分)经市场调查,某种优质西瓜质量为(5±0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A、B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗,记录它们的质量如下(单位:kg):
A:4.1 4.8 5.4 4.9 4.7 5.0 4.9 4.8 5.8 5.2
5.0 4.8 5.2 4.9 5.2 5.0 4.8 5.2 5.1 5.0
B:4.5 4.9 4.8 4.5 5.2 5.1 5.0 4.5 4.7 4.9
5.4 5.5 4.6 5.3 4.8 5.0 5.2 5.3 5.0 5.3
(1)若质量为(5±0.25)kg的为优等品,根据以上信息完成下表:
优等品数量(颗) 平均数 方差
A 4.990 0.103
B 4.975 0.093
(2)请分别从优等品数量、平均数与方差三方面对A、B两种技术作出评价;从市场销售的角度看,你认为推广哪种种植技术较好.
23、(10分) 在一次课外实践活动中,同学们要测量某公园人工湖两侧两个凉亭之间的距离.现测得m,m,,请计算两个凉亭之间的距离.
24、(14分)已知:△ABC,M为AB中点, MD交AC于F,交BC延长线于D;ME交BC于G,交AC延长线于E. ∠DME=∠A=∠B=α.(1)求证:△AMF∽△BGM(2)如果α=45°,AB=AF=3,求FG的长。
答案:
一、(36分)
1—6DCBCCB;7—12BDDDCA
二、(20分)13、三;14、;15、;16、1:3;17、没有一个内角小于或等于60°。
三、(64分)18、(8分)(1)12;(2)1.
19、(8分)PD=2.
解法1:作PE⊥OB,垂足为E。
∵ P在∠AOB的平分线上,PE⊥OB, PD⊥OA.
∴PD=PE
∵ PC∥OA
∴∠BCP=∠BOA=30°,在Rt△PCE中,PE=PC×sin∠BCP=4×0.5=2
∴PD=2
解法2:作CF⊥OA于F。易证OC=CP=4,故PD=CF=2.
20、(8分)
解法1:
21、(8分)。提示:证△BDE∽△BCA
22、解:(1)依次为16颗,10颗 3分
(2)从优等品数量的角度看,因A技术种植的西瓜优等品数量较多,所以A技术较好;
4分
从平均数的角度看,因A技术种植的西瓜质量的平均数更接近5kg,所以A技术较好;
5分
从方差的角度看,因B技术种植的西瓜质量的方差更小,所以B技术种植的西瓜质量更为稳定; 6分
从市场销售角度看,因优等品更畅销,A技术种植的西瓜优等品数量更多,且平均质量更接近5kg,因而更适合推广A种技术 8分
说明:
1.第(1)问中,答对1个得2分,答对2个得3分;
2.6分~8分给分处,答B种技术种植的西瓜质量较稳定,更适合推广B种技术的给1分.
23、(10分)解:如图,过点作⊥,交的延长线于点. 2分
在中,. 4分
sinsin.
coscos=15.
又在中,
,
. 9分
,
答:两个凉亭之间的距离为50m. 10分
24、解:由题知,
,
而,
又,
.
∴△AMF∽△BGM. 6分
(2)解:当α=45°时,可得AC⊥BC且AC=BC,
∵M为AB中点,∴AM=BM=. 8分
由,得.
∴. 12分
又,∴,
∴. 14分
O
C
A
B
x
1
4题图
10题图
2题图
12题图
16题图
21题图
19题图
A
B
C
D
A
B
C
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 6 页) 版权所有@21世纪教育网
初二下学期期末试题(青岛版)
一、选择题(36分)
1、下面计算正确的是( )
A.;B.;C.;D.
2、如图,数轴上与1,对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则( )
A. B. C. D.2
3、去年,我国首例甲型H1N1流感确诊病例在成都某医院隔离观察,要掌握一周内体温是否稳定,则医生要了解这位病人7天体温的( )。
A.众数 B.方差 C.平均数 D.中位数
4、已知:如图,已知AB=AD,则添加条件( )后,仍无法判定△ABC≌△ADC。
A.CB=CD; B.∠BAC=∠DAC; C.∠BCA=∠DCA; D.∠B=∠D=90°
5、若一组数据x1,x2,x3,……,xn的方差为0。则必有( )
A.平均数为0;B.这组数据均为0;C.这组数据都相等;D.中位数为0
6、下列根式中与是同类二次根式的是( )。
A. ;B. ;C. ;D.
7、在Rt△ABC中, ∠C=90°, 那么a3cosA+b3cosB=( )
A.a3 B.abc C.(a+b)c2 D.
8、一条斜坡公路坡度为i=1:3,这段公路长100米,则坡底到坡顶这段公路升高( )米。
A.30;B.10;C.;D.。
9、△ABC中,P为AB上一点,下列四个条件:(1)∠ACP=∠B;(2)∠APC=∠ACB;(3)AC2=AP×AB;(4).只添加其中一个条件,能使△APC∽△ACB的条件可以是( )。A.(1)(2)(4);B.(1)(3)(4);C.(2)(3)(4);D.(1)(2)(3)。
10、如图,已知:∠AOD=90°,OA=OB=BC=CD,则下列结论成立的是( )
A.△OAB∽△OCA;B.△OAB∽△ODA;C.△ABC∽△ACD;D.△ABC∽△DBA
11、下列命题:(1)如果a2=b2,那么a=b;(2)如果△ABC的三边满足:a2+b2=c2,那么∠C=90°;(3)如果,那么a、b互为相反数;(4)如果两个直角三角形全等,那么这两个直角三角形有两边对应相等。逆命题正确的有( )个。
A.1;B.2;C.3;D.4
12、Rt△ABC中,∠B=90°,AB=6,BC=8。将△ABC沿DE折叠,使C落在AB边F处,且DF∥BC,则CD=( )
二、填空题(20分)
13、代数式则P(m,n)在直角坐标系的第________象限。
14、等腰三角形两边长为4cm,6cm.则底角的余弦值为_____________.
15、一直角三角形两边为,则第三边为____________.
16、将一副三角板如图叠放,∠D=30°,∠A=45°,则△AOB与△DOC的面积比为______.
17、用反证法证明:在三角形中至少有一个内角小于或等于60°时,第一步
应假设:________________________________________________。
三、解答题(64分)
18、(8分)计算:
19、(8分)已知:如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,PC=4。求:PD的长。
20、(8分)
21、(8分)在Rt△ABC中,∠ACB=90°,BC=3,AC=4。AB的垂直平分线DE交BC的延长线于点E,求CE的长。
22、(8分)经市场调查,某种优质西瓜质量为(5±0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A、B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗,记录它们的质量如下(单位:kg):
A:4.1 4.8 5.4 4.9 4.7 5.0 4.9 4.8 5.8 5.2
5.0 4.8 5.2 4.9 5.2 5.0 4.8 5.2 5.1 5.0
B:4.5 4.9 4.8 4.5 5.2 5.1 5.0 4.5 4.7 4.9
5.4 5.5 4.6 5.3 4.8 5.0 5.2 5.3 5.0 5.3
(1)若质量为(5±0.25)kg的为优等品,根据以上信息完成下表:
优等品数量(颗) 平均数 方差
A 4.990 0.103
B 4.975 0.093
(2)请分别从优等品数量、平均数与方差三方面对A、B两种技术作出评价;从市场销售的角度看,你认为推广哪种种植技术较好.
23、(10分) 在一次课外实践活动中,同学们要测量某公园人工湖两侧两个凉亭之间的距离.现测得m,m,,请计算两个凉亭之间的距离.
24、(14分)已知:△ABC,M为AB中点, MD交AC于F,交BC延长线于D;ME交BC于G,交AC延长线于E. ∠DME=∠A=∠B=α.(1)求证:△AMF∽△BGM(2)如果α=45°,AB=AF=3,求FG的长。
答案:
一、(36分)
1—6DCBCCB;7—12BDDDCA
二、(20分)13、三;14、;15、;16、1:3;17、没有一个内角小于或等于60°。
三、(64分)18、(8分)(1)12;(2)1.
19、(8分)PD=2.
解法1:作PE⊥OB,垂足为E。
∵ P在∠AOB的平分线上,PE⊥OB, PD⊥OA.
∴PD=PE
∵ PC∥OA
∴∠BCP=∠BOA=30°,在Rt△PCE中,PE=PC×sin∠BCP=4×0.5=2
∴PD=2
解法2:作CF⊥OA于F。易证OC=CP=4,故PD=CF=2.
20、(8分)
解法1:
21、(8分)。提示:证△BDE∽△BCA
22、解:(1)依次为16颗,10颗 3分
(2)从优等品数量的角度看,因A技术种植的西瓜优等品数量较多,所以A技术较好;
4分
从平均数的角度看,因A技术种植的西瓜质量的平均数更接近5kg,所以A技术较好;
5分
从方差的角度看,因B技术种植的西瓜质量的方差更小,所以B技术种植的西瓜质量更为稳定; 6分
从市场销售角度看,因优等品更畅销,A技术种植的西瓜优等品数量更多,且平均质量更接近5kg,因而更适合推广A种技术 8分
说明:
1.第(1)问中,答对1个得2分,答对2个得3分;
2.6分~8分给分处,答B种技术种植的西瓜质量较稳定,更适合推广B种技术的给1分.
23、(10分)解:如图,过点作⊥,交的延长线于点. 2分
在中,. 4分
sinsin.
coscos=15.
又在中,
,
. 9分
,
答:两个凉亭之间的距离为50m. 10分
24、解:由题知,
,
而,
又,
.
∴△AMF∽△BGM. 6分
(2)解:当α=45°时,可得AC⊥BC且AC=BC,
∵M为AB中点,∴AM=BM=. 8分
由,得.
∴. 12分
又,∴,
∴. 14分
O
C
A
B
x
1
4题图
10题图
2题图
12题图
16题图
21题图
19题图
A
B
C
D
A
B
C
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 6 页) 版权所有@21世纪教育网
同课章节目录
