三角形全等的条件(一)
图片预览



文档简介
课件24张PPT。5.4 探索三角形全等的条件(一)
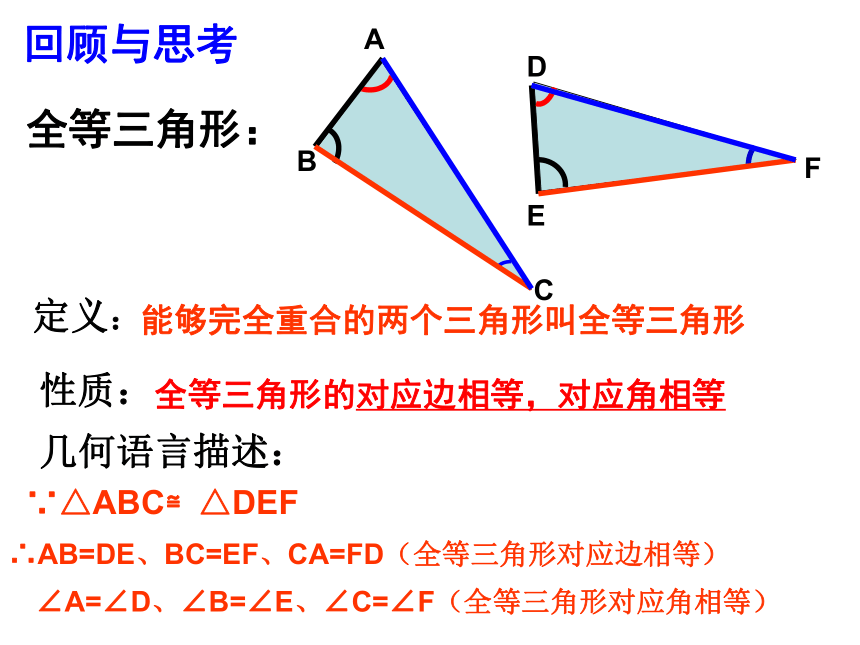
授课老师:马海英全等三角形的对应边相等,对应角相等全等三角形:能够完全重合的两个三角形叫全等三角形回顾与思考几何语言描述:∵△ABC≌△DEF∴AB=DE、BC=EF、CA=FD(全等三角形对应边相等)∠A=∠D、∠B=∠E、∠C=∠F(全等三角形对应角相等)定义:性质:AFEDCB情境问题: 为庆祝“五·四”青年节,班长想要同学们回家制作三角形彩旗(如图所示),那么,班长应提供多少个数据,能保证同学们制作出来的三角形彩旗形状、大小一模一样呢?数据能尽可能少吗?一个条件: (1)一个角
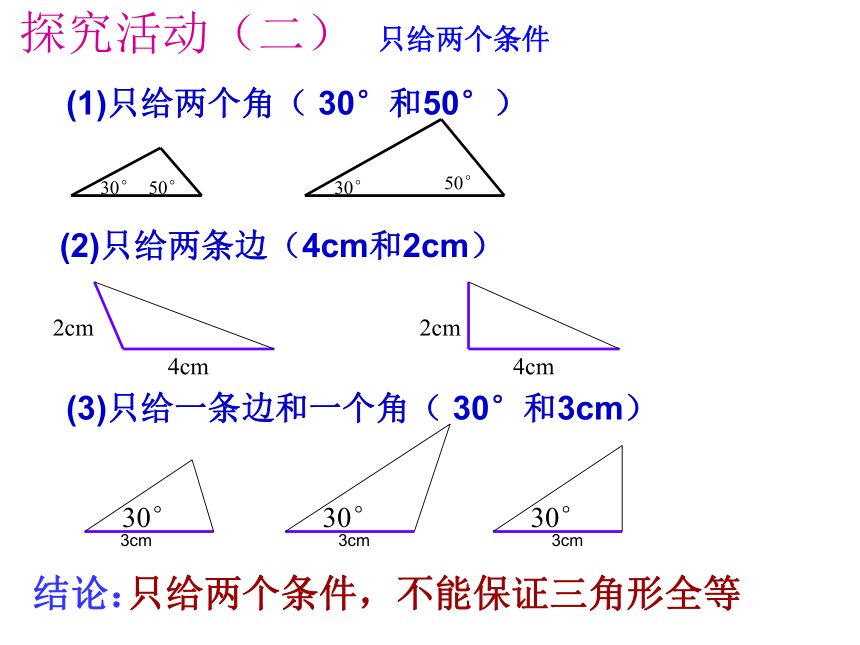
(2)一条边两个条件: (1)两个角
(2)两条边
(3)一个角和一条边三个条件: (1)三个角
(2)三条边
(3)两角一边
(4)两边一角
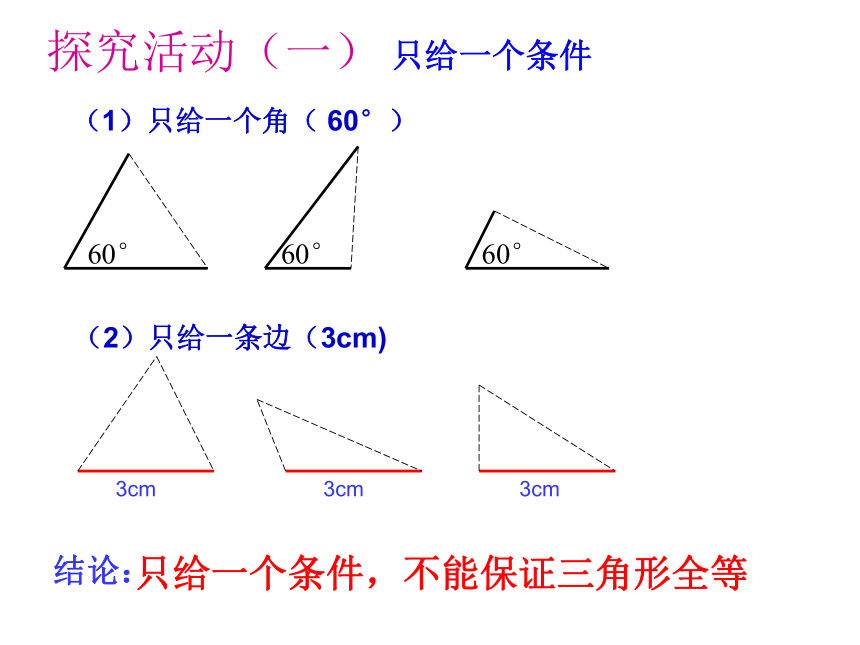
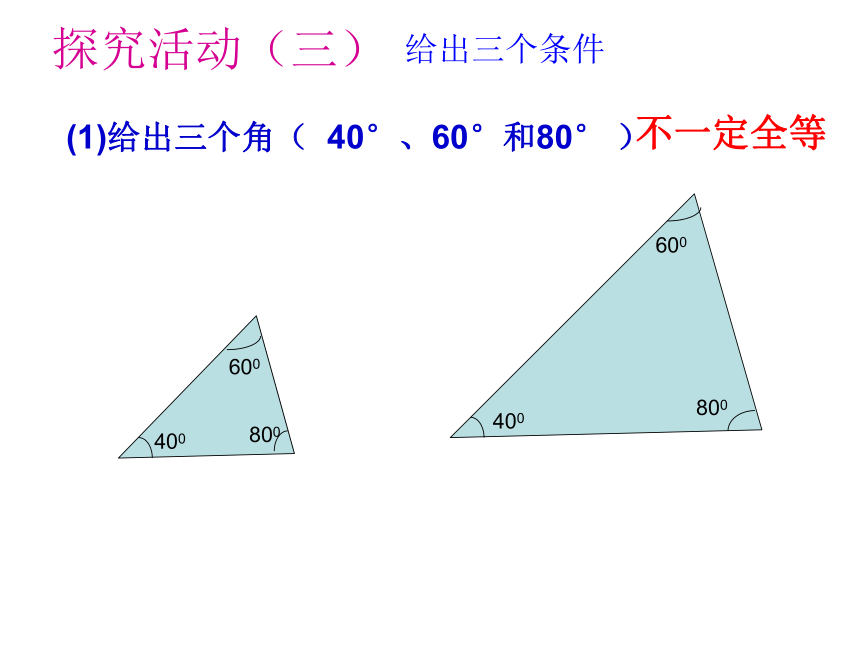
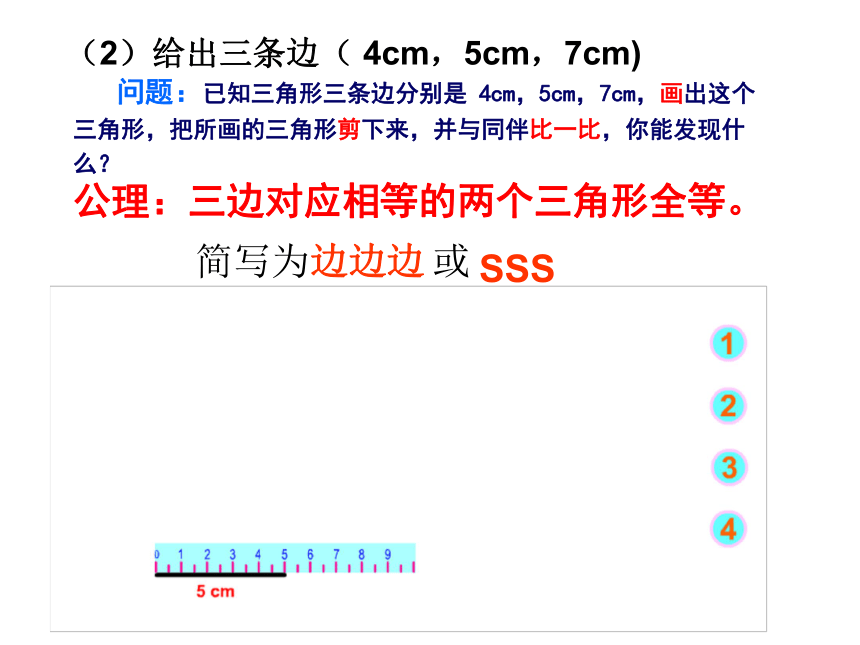
……探究活动(一)只给一个条件(1)只给一个角( 60°) (2)只给一条边(3cm) 3cm 3cm 3cm结论:只给一个条件,不能保证三角形全等探究活动(二)只给两个条件(1)只给两个角( 30°和50°)(2)只给两条边(4cm和2cm)(3)只给一条边和一个角( 30°和3cm)结论:只给两个条件,不能保证三角形全等3cm 3cm 3cm探究活动(三)给出三个条件(1)给出三个角( 40°、60°和80° )不一定全等400400600800600800 问题:已知三角形三条边分别是 4cm,5cm,7cm,画出这个三角形,把所画的三角形剪下来,并与同伴比一比,你能发现什么?公理:三边对应相等的两个三角形全等。(2)给出三条边( 4cm,5cm,7cm)简写为边边边或SSSABCDEF在△ABC和△DEF中AB=DEBC=EFAC=DF∴ △ABC ≌ △DEF (SSS)三角形全等书写一般步骤:1、写出在哪两个三角形中2、摆出的三个条件用大括号 括起来3、写出全等结论例1、如右图,△ABC是一个钢架,AB=AC,AD是连接A与BC的中点D的支架。 求证:(1)△ ABD≌ △ ACD
(2) ∠B=∠C分析:要证明两个三角形全等,首先看它们的三边是否对应相等。证明:∵D是BC中点∴BD=CD在△ ABD和△ ACD中AB=AC(已知)BD=CD(已证)AD=AD∴ △ ABD≌ △ ACD(SSS)(公共边)(1)(2)由(1)知△ABD≌△ACD∴ ∠B=∠C(全等三角形对应角相等)练一练1、如图,AB=AD,BC=DC,试证明△ABC和△ADC全等。证明:在△ABC和△ADC中
AB=AD(已知)
BC=CD(已知)
= ( )
∴ △ABC △ADC( ) ACAC公共边≌SSS巩固新知1、如图,在四边形ABCD中,AB=CD, AD=BC
求证:(1)△ABD≌△CDB (2)∠ADB=∠CBD2、 如图,已知AC=FE,BC=DE,点A,D,B, F在一条
直线上 AD=FB,你觉得△ ABC和△ FDE全等吗?如果全等,请说明理由。ADCEFB 证明:(1)在△ABD和△CDB 中
AB=CD(已知)
AD=BC(已知)
DB=BD(公共边)
∴ △ABD≌△CDB (SSS)
(2)由(1)知△ABD≌△CDB
∴∠ADB=∠CBD(全等三角形对应角相等)
解: △ ABC≌△ FDE ,理由是:
∵ AD=FB
∴ AD+DB=FB+DB
即 AB=FD
在△ ABC和△ FDE中
AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴ △ ABC≌ △ FDE (SSS) 由上面的结论可知,只要三角形三边长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三角形稳定性。三角形的稳定性: 四边形不具有稳定性,你能想出什么方法
让它们的形状不发生改变吗? 试一试请同学们谈谈本节课的收获与体会本节课你学到了什么?
有什么收获?
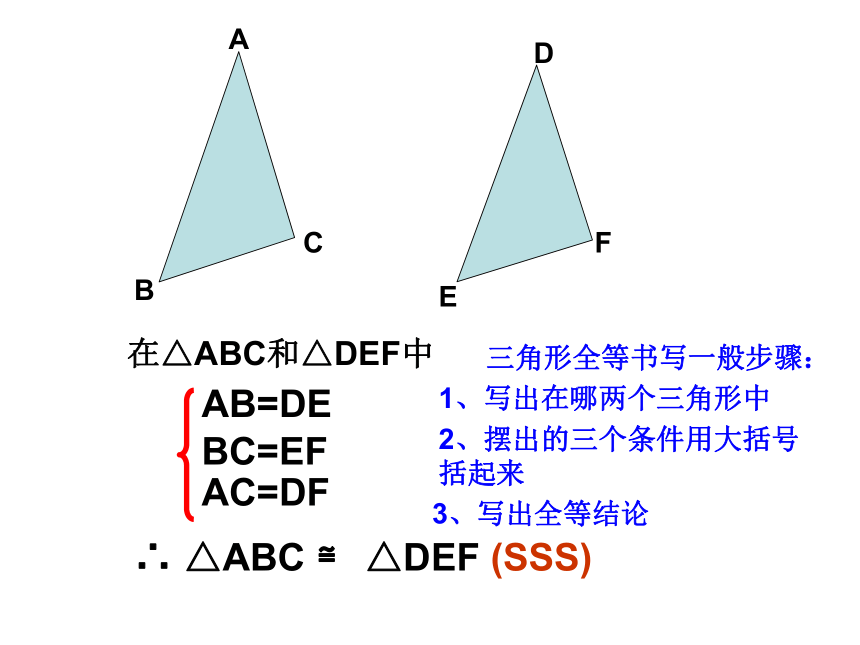
还存在什么没有解决的问题? 在△ABC和△DEF中
AB=DE
BC=EF
AC=DF
∴ △ABC ≌ △DEF (SSS)ADCEFB公理: 三边对应相等的两个三角形全等, 简写成边边边或SSS
三角形全等书写的一般步骤:
① 写出在哪两个三角形中
②摆出三个条件用大括号括起来
③写出全等结论小结:作业:2、如图,已知△ BOD≌ △ COE,AD=AE
求证: △ ABE≌ △ ACD
1、如图,线段AB、CD交于点O,
AD=CB,OA=OC,AB=CD;
求证: ∠A=∠CABCDOABCDEO再见
授课老师:马海英全等三角形的对应边相等,对应角相等全等三角形:能够完全重合的两个三角形叫全等三角形回顾与思考几何语言描述:∵△ABC≌△DEF∴AB=DE、BC=EF、CA=FD(全等三角形对应边相等)∠A=∠D、∠B=∠E、∠C=∠F(全等三角形对应角相等)定义:性质:AFEDCB情境问题: 为庆祝“五·四”青年节,班长想要同学们回家制作三角形彩旗(如图所示),那么,班长应提供多少个数据,能保证同学们制作出来的三角形彩旗形状、大小一模一样呢?数据能尽可能少吗?一个条件: (1)一个角
(2)一条边两个条件: (1)两个角
(2)两条边
(3)一个角和一条边三个条件: (1)三个角
(2)三条边
(3)两角一边
(4)两边一角
……探究活动(一)只给一个条件(1)只给一个角( 60°) (2)只给一条边(3cm) 3cm 3cm 3cm结论:只给一个条件,不能保证三角形全等探究活动(二)只给两个条件(1)只给两个角( 30°和50°)(2)只给两条边(4cm和2cm)(3)只给一条边和一个角( 30°和3cm)结论:只给两个条件,不能保证三角形全等3cm 3cm 3cm探究活动(三)给出三个条件(1)给出三个角( 40°、60°和80° )不一定全等400400600800600800 问题:已知三角形三条边分别是 4cm,5cm,7cm,画出这个三角形,把所画的三角形剪下来,并与同伴比一比,你能发现什么?公理:三边对应相等的两个三角形全等。(2)给出三条边( 4cm,5cm,7cm)简写为边边边或SSSABCDEF在△ABC和△DEF中AB=DEBC=EFAC=DF∴ △ABC ≌ △DEF (SSS)三角形全等书写一般步骤:1、写出在哪两个三角形中2、摆出的三个条件用大括号 括起来3、写出全等结论例1、如右图,△ABC是一个钢架,AB=AC,AD是连接A与BC的中点D的支架。 求证:(1)△ ABD≌ △ ACD
(2) ∠B=∠C分析:要证明两个三角形全等,首先看它们的三边是否对应相等。证明:∵D是BC中点∴BD=CD在△ ABD和△ ACD中AB=AC(已知)BD=CD(已证)AD=AD∴ △ ABD≌ △ ACD(SSS)(公共边)(1)(2)由(1)知△ABD≌△ACD∴ ∠B=∠C(全等三角形对应角相等)练一练1、如图,AB=AD,BC=DC,试证明△ABC和△ADC全等。证明:在△ABC和△ADC中
AB=AD(已知)
BC=CD(已知)
= ( )
∴ △ABC △ADC( ) ACAC公共边≌SSS巩固新知1、如图,在四边形ABCD中,AB=CD, AD=BC
求证:(1)△ABD≌△CDB (2)∠ADB=∠CBD2、 如图,已知AC=FE,BC=DE,点A,D,B, F在一条
直线上 AD=FB,你觉得△ ABC和△ FDE全等吗?如果全等,请说明理由。ADCEFB 证明:(1)在△ABD和△CDB 中
AB=CD(已知)
AD=BC(已知)
DB=BD(公共边)
∴ △ABD≌△CDB (SSS)
(2)由(1)知△ABD≌△CDB
∴∠ADB=∠CBD(全等三角形对应角相等)
解: △ ABC≌△ FDE ,理由是:
∵ AD=FB
∴ AD+DB=FB+DB
即 AB=FD
在△ ABC和△ FDE中
AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴ △ ABC≌ △ FDE (SSS) 由上面的结论可知,只要三角形三边长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三角形稳定性。三角形的稳定性: 四边形不具有稳定性,你能想出什么方法
让它们的形状不发生改变吗? 试一试请同学们谈谈本节课的收获与体会本节课你学到了什么?
有什么收获?
还存在什么没有解决的问题? 在△ABC和△DEF中
AB=DE
BC=EF
AC=DF
∴ △ABC ≌ △DEF (SSS)ADCEFB公理: 三边对应相等的两个三角形全等, 简写成边边边或SSS
三角形全等书写的一般步骤:
① 写出在哪两个三角形中
②摆出三个条件用大括号括起来
③写出全等结论小结:作业:2、如图,已知△ BOD≌ △ COE,AD=AE
求证: △ ABE≌ △ ACD
1、如图,线段AB、CD交于点O,
AD=CB,OA=OC,AB=CD;
求证: ∠A=∠CABCDOABCDEO再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
