二次函数单元测试卷
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
二次函数单元测试卷
选择题(本大题共10小题,每小题3分,共30分)
1.下列函数不属于二次函数的是( )
A.y=(x-1)(x+2) B.y=(x+1)2 C. y=1-x2 D. y=2(x+3)2-2x2
2. y=mxm2+3m+2是二次函数,则m的值为( )
A、0,-3 B、0,3 C、0 D、-3
3. 抛物线的顶点坐标是( )
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
4. y=(x-1)2+2的对称轴是直线( )
A.x=-1 B.x=1 C.y=-1 D.y=1
5.已知二次函数的图象经过原点,则的值为 ( )
A. 0或2 B. 0 C. 2 D.无法确定
6. 二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
A. y=x2+3 B. y=x2-3 C. y=(x+3)2 D. y=(x-3)2
7.函数y=2x2-3x+4经过的象限是( )
A.一、二、三象限 B.一、二象限 C.三、四象限 D.一、二、四象限
8.下列说法错误的是( )
A.二次函数y=3x2中,当x>0时,y随x的增大而增大
B.二次函数y=-6x2中,当x=0时,y有最大值0
C.a越大图象开口越小,a越小图象开口越大
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
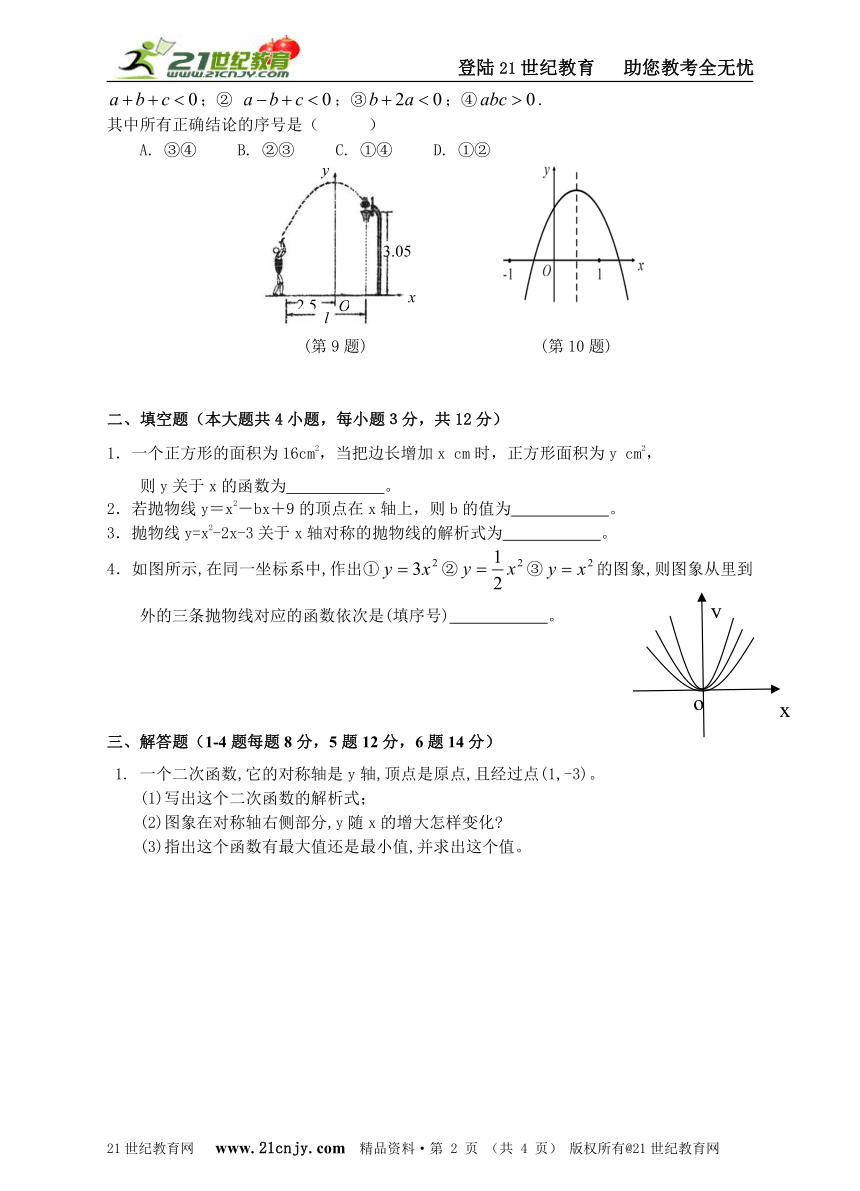
9.如图,小芳在某次投篮中,球的运动路线是抛物线y=-x2+3.5的一部分,若命中篮圈中心,则他与篮底的距离l是( )
A.3.5m B.4m C.4.5m D.4.6m
10.已知二次函数的图象如图所示,给出以下结论:① ;② ;③;④.
其中所有正确结论的序号是( )
A. ③④ B. ②③ C. ①④ D. ①②
(第9题) (第10题)
二、填空题(本大题共4小题,每小题3分,共12分)
1.一个正方形的面积为16cm2,当把边长增加x cm时,正方形面积为y cm2,
则y关于x的函数为 。
2.若抛物线y=x2-bx+9的顶点在x轴上,则b的值为 。
3.抛物线y=x2-2x-3关于x轴对称的抛物线的解析式为 。
4.如图所示,在同一坐标系中,作出①②③的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) 。
解答题(1-4题每题8分,5题12分,6题14分)
1. 一个二次函数,它的对称轴是y轴,顶点是原点,且经过点(1,-3)。
(1)写出这个二次函数的解析式;
(2)图象在对称轴右侧部分,y随x的增大怎样变化
(3)指出这个函数有最大值还是最小值,并求出这个值。
2.拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为m时,水面的宽度为多少米?
3. 如图二次函数的图象经过和两点,且交轴于点.
(1)试确定、的值;
(2)过点作轴交抛物线于点点为此抛物线的顶点,试确定的形状.
4. 已知二次函数中的满足下表:
… 0 1 2 …
… 4 0 0 …
求这个二次函数关系式.
5. 某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
6. 如图,已知一个三角形纸片,边的长为8,边上的高为,和都为锐角,为一动点(点与点不重合),过点作,交于点,在中,设的长为,上的高为.
(1)请你用含的代数式表示.
(2)将沿折叠,使落在四边形所在平面,设点落在平面的点为,与四边形重叠部分的面积为,当为何值时,最大,最大值为多少?
2.5m
3.05m
x
y
o
0
x
y
A
B
C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
二次函数单元测试卷
选择题(本大题共10小题,每小题3分,共30分)
1.下列函数不属于二次函数的是( )
A.y=(x-1)(x+2) B.y=(x+1)2 C. y=1-x2 D. y=2(x+3)2-2x2
2. y=mxm2+3m+2是二次函数,则m的值为( )
A、0,-3 B、0,3 C、0 D、-3
3. 抛物线的顶点坐标是( )
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
4. y=(x-1)2+2的对称轴是直线( )
A.x=-1 B.x=1 C.y=-1 D.y=1
5.已知二次函数的图象经过原点,则的值为 ( )
A. 0或2 B. 0 C. 2 D.无法确定
6. 二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
A. y=x2+3 B. y=x2-3 C. y=(x+3)2 D. y=(x-3)2
7.函数y=2x2-3x+4经过的象限是( )
A.一、二、三象限 B.一、二象限 C.三、四象限 D.一、二、四象限
8.下列说法错误的是( )
A.二次函数y=3x2中,当x>0时,y随x的增大而增大
B.二次函数y=-6x2中,当x=0时,y有最大值0
C.a越大图象开口越小,a越小图象开口越大
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
9.如图,小芳在某次投篮中,球的运动路线是抛物线y=-x2+3.5的一部分,若命中篮圈中心,则他与篮底的距离l是( )
A.3.5m B.4m C.4.5m D.4.6m
10.已知二次函数的图象如图所示,给出以下结论:① ;② ;③;④.
其中所有正确结论的序号是( )
A. ③④ B. ②③ C. ①④ D. ①②
(第9题) (第10题)
二、填空题(本大题共4小题,每小题3分,共12分)
1.一个正方形的面积为16cm2,当把边长增加x cm时,正方形面积为y cm2,
则y关于x的函数为 。
2.若抛物线y=x2-bx+9的顶点在x轴上,则b的值为 。
3.抛物线y=x2-2x-3关于x轴对称的抛物线的解析式为 。
4.如图所示,在同一坐标系中,作出①②③的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) 。
解答题(1-4题每题8分,5题12分,6题14分)
1. 一个二次函数,它的对称轴是y轴,顶点是原点,且经过点(1,-3)。
(1)写出这个二次函数的解析式;
(2)图象在对称轴右侧部分,y随x的增大怎样变化
(3)指出这个函数有最大值还是最小值,并求出这个值。
2.拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为m时,水面的宽度为多少米?
3. 如图二次函数的图象经过和两点,且交轴于点.
(1)试确定、的值;
(2)过点作轴交抛物线于点点为此抛物线的顶点,试确定的形状.
4. 已知二次函数中的满足下表:
… 0 1 2 …
… 4 0 0 …
求这个二次函数关系式.
5. 某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
6. 如图,已知一个三角形纸片,边的长为8,边上的高为,和都为锐角,为一动点(点与点不重合),过点作,交于点,在中,设的长为,上的高为.
(1)请你用含的代数式表示.
(2)将沿折叠,使落在四边形所在平面,设点落在平面的点为,与四边形重叠部分的面积为,当为何值时,最大,最大值为多少?
2.5m
3.05m
x
y
o
0
x
y
A
B
C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
