新课标A版选修四新课标A版选修4-4直线的极坐标方程
文档属性
| 名称 | 新课标A版选修四新课标A版选修4-4直线的极坐标方程 |
|
|
| 格式 | rar | ||
| 文件大小 | 139.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-16 00:00:00 | ||
图片预览





文档简介
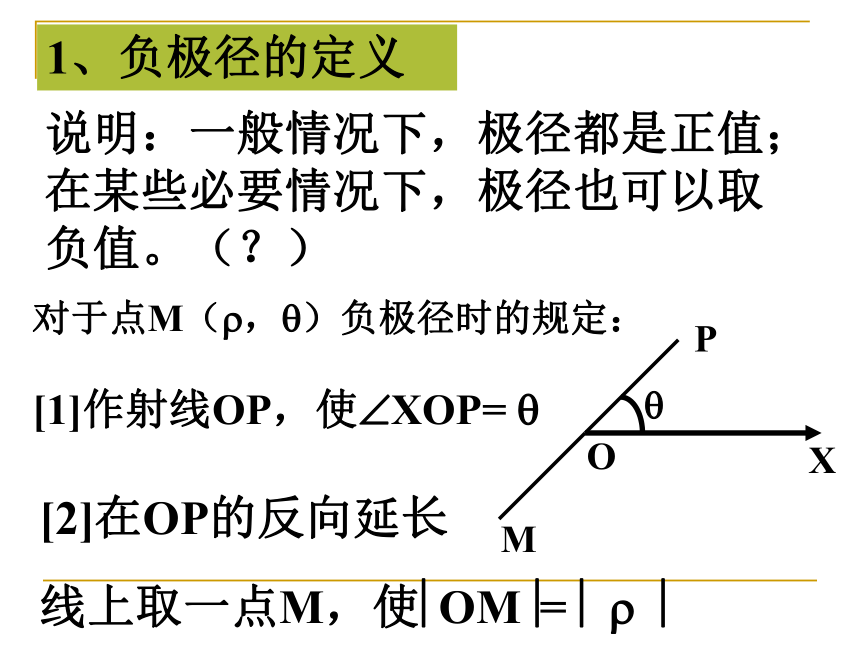
课件13张PPT。1、负极径的定义说明:一般情况下,极径都是正值;在某些必要情况下,极径也可以取负值。(?)对于点M(?,?)负极径时的规定:[1]作射线OP,使?XOP= ?[2]在OP的反向延长
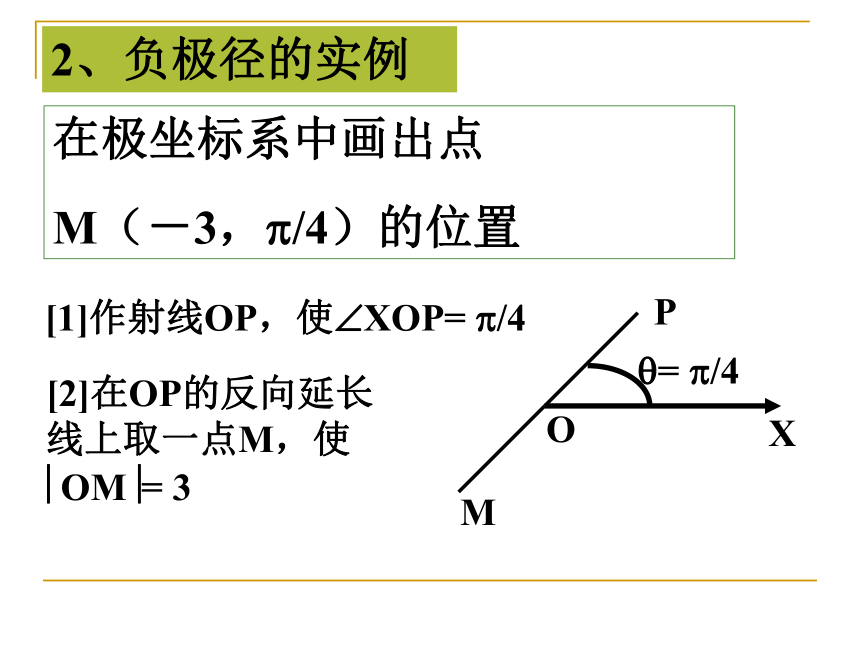
线上取一点M,使?OM?= ? ? ?2、负极径的实例在极坐标系中画出点
M(-3,?/4)的位置[1]作射线OP,使?XOP= ?/4 [2]在OP的反向延长线上取一点M,使?OM?= 3负极径小结:极径变为负,极角增加 ? 。答:(-6, +π)或(-6,- +π)特别强调:一般情况下(若不作特别说明时),认为? ≥ 0 。因为负极径只在极少数情况用。例题1:求过极点,倾角为 的射线的极坐标方程。分析:如图,所求的射线上任一点的极角都是 ,其极径可以取任意的非负数。故所求直线的极坐标方程为新课讲授1、求过极点,倾角为 的射线的极坐标方程。易得思考:2、求过极点,倾角为 的直线的极坐标方程。 和前面的直角坐标系里直线方程的表示形式比较起来,极坐标系里的直线表示起来很不方便,要用两条射线组合而成。原因在哪?为了弥补这个不足,可以考虑允许极径可以取全体实数。则上面的直线的极坐标方程可以表示为或新课引入:思考:在平面直角坐标系中1、过点(3,0)且与x轴垂直的直线方程为 ;过点(3,3)且与x轴垂直的直线方程为 x=3x=32、过点(a,b)且垂直于x轴的直线方程为_______x=a特点:所有点的横坐标都是一样,纵坐标可以取任意值。例题2、求过点A(a,0)(a>0),且垂直于极轴的直线L的极坐标方程。解:如图,设点为直线L上除点A外的任意一点,连接OM在 中有 即可以验证,点A的坐标也满足上式。求直线的极坐标方程步骤1、根据题意画出草图;2、设点 是直线上任意一点;3、连接MO;4、根据几何条件建立关于 的方 程,并化简;5、检验并确认所得的方程即为所求。练习:设点A的极坐标为 ,直线 过点A且与极轴所成的角为 ,求直线 的极坐标方程。 解:如图,设点为直线 上异于的点连接OM,在 中有 即显然A点也满足上方程。例题3设点P的极坐标为 ,直线 过点P且与极轴所成的角为 ,求直线 的极坐标方程。 则 由点P的极坐标知 由正弦定理得显然点P的坐标也是它的解。小结:直线的几种极坐标方程1、过极点2、过某个定点,且垂直于极轴3、过某个定点,且与极轴成一定
的角度
线上取一点M,使?OM?= ? ? ?2、负极径的实例在极坐标系中画出点
M(-3,?/4)的位置[1]作射线OP,使?XOP= ?/4 [2]在OP的反向延长线上取一点M,使?OM?= 3负极径小结:极径变为负,极角增加 ? 。答:(-6, +π)或(-6,- +π)特别强调:一般情况下(若不作特别说明时),认为? ≥ 0 。因为负极径只在极少数情况用。例题1:求过极点,倾角为 的射线的极坐标方程。分析:如图,所求的射线上任一点的极角都是 ,其极径可以取任意的非负数。故所求直线的极坐标方程为新课讲授1、求过极点,倾角为 的射线的极坐标方程。易得思考:2、求过极点,倾角为 的直线的极坐标方程。 和前面的直角坐标系里直线方程的表示形式比较起来,极坐标系里的直线表示起来很不方便,要用两条射线组合而成。原因在哪?为了弥补这个不足,可以考虑允许极径可以取全体实数。则上面的直线的极坐标方程可以表示为或新课引入:思考:在平面直角坐标系中1、过点(3,0)且与x轴垂直的直线方程为 ;过点(3,3)且与x轴垂直的直线方程为 x=3x=32、过点(a,b)且垂直于x轴的直线方程为_______x=a特点:所有点的横坐标都是一样,纵坐标可以取任意值。例题2、求过点A(a,0)(a>0),且垂直于极轴的直线L的极坐标方程。解:如图,设点为直线L上除点A外的任意一点,连接OM在 中有 即可以验证,点A的坐标也满足上式。求直线的极坐标方程步骤1、根据题意画出草图;2、设点 是直线上任意一点;3、连接MO;4、根据几何条件建立关于 的方 程,并化简;5、检验并确认所得的方程即为所求。练习:设点A的极坐标为 ,直线 过点A且与极轴所成的角为 ,求直线 的极坐标方程。 解:如图,设点为直线 上异于的点连接OM,在 中有 即显然A点也满足上方程。例题3设点P的极坐标为 ,直线 过点P且与极轴所成的角为 ,求直线 的极坐标方程。 则 由点P的极坐标知 由正弦定理得显然点P的坐标也是它的解。小结:直线的几种极坐标方程1、过极点2、过某个定点,且垂直于极轴3、过某个定点,且与极轴成一定
的角度
