平均变化率
图片预览





文档简介
课件24张PPT。1.1平均变化率石塔寺银杏树
树高:15米
树龄:1200年雨后春笋
高:15厘米
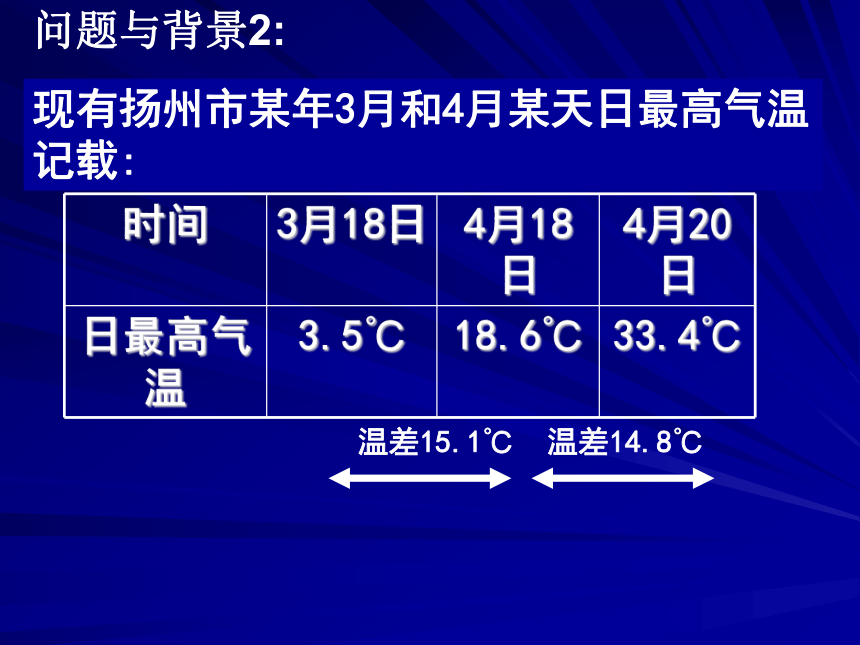
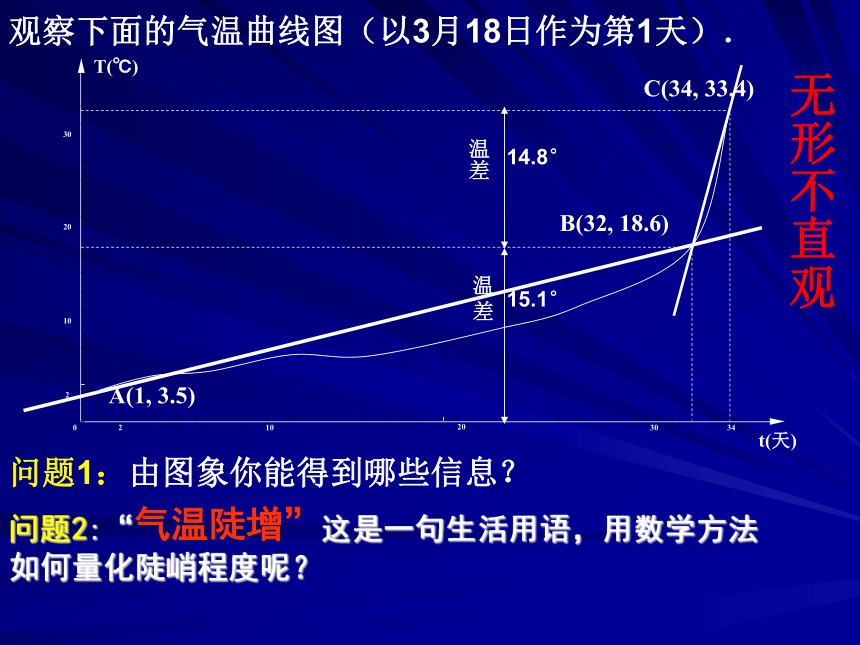
时间:两天问题与背景1:现有扬州市某年3月和4月某天日最高气温记载:温差15.1℃温差14.8℃问题与背景2:观察下面的气温曲线图(以3月18日作为第1天).问题1:由图象你能得到哪些信息?无形不直观21020300C(34, 33.4)T(℃)t(天)问题2:“气温陡增”这是一句生活用语,用数学方法如何量化陡峭程度呢?平均变化率的定义:一般地,函数 在区间 上的平均
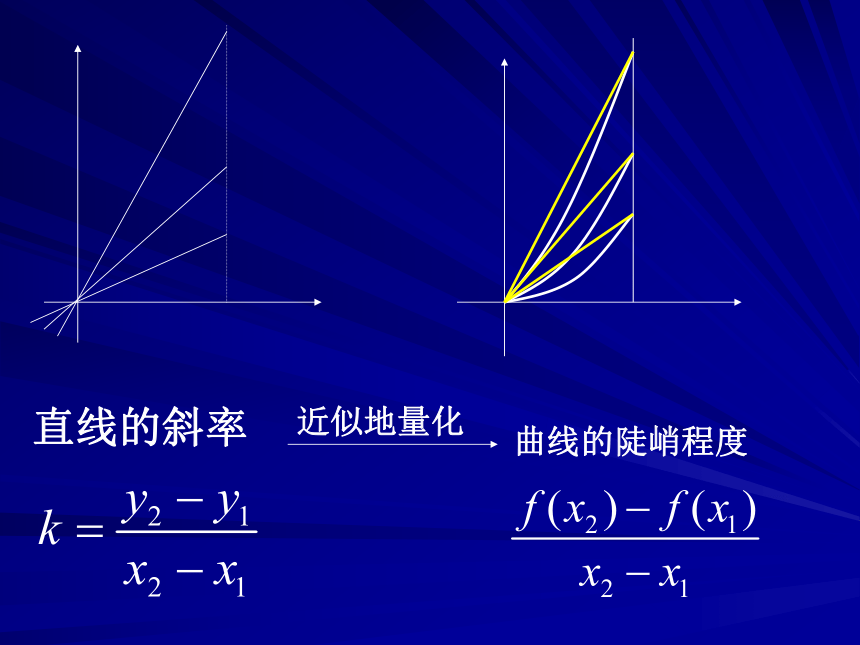
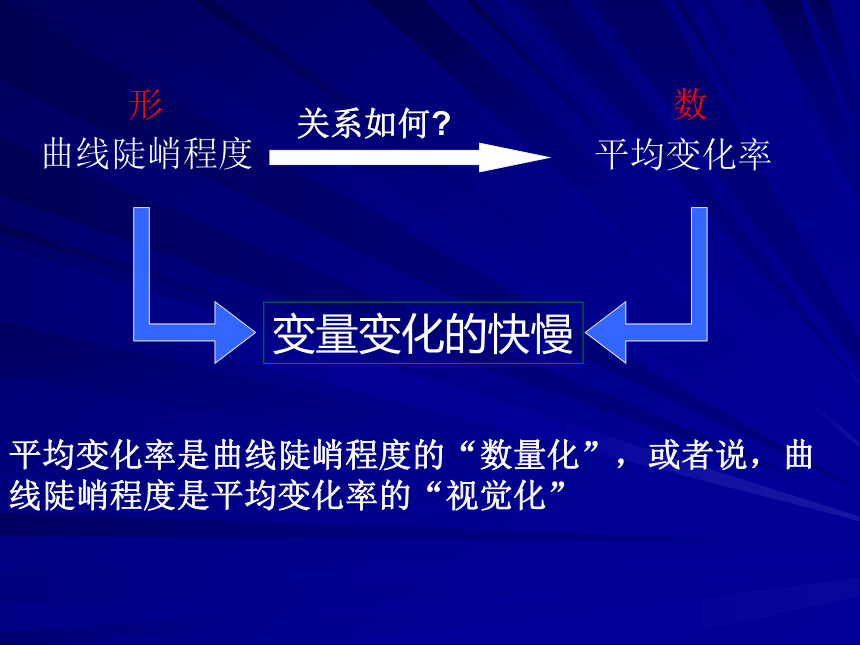
变化率为:数学应用:1:某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率。解:(1)从出生到第3个月,婴儿体重平均变化率为:(2)平均变化率是曲线陡峭程度的“数量化”,或者说,曲线陡峭程度是平均变化率的“视觉化”关系如何?1.试求出CD、DE段上的平均变化率.2.你是怎样理解“—”号的?2030342102030A(1, 3.5)B(32, 18.6)0C(34, 33.4)T(℃)t(天)图4-1-1210D(37,27.7)E(40,27.1)例2:水经过虹吸管从容器甲中流向容器乙,t秒后容器甲中水的体积V(t)=5e-0.1t
(单位cm3),计算第一个10秒内V的平均变化率.解:在区间[0,10]上,体积的平均变化率为:数学应用:问题引申1:怎样解释结果中的“-”号?
问题引申2:若研究对象改为乙,此时平均变化率的正负号如何?
问题引申3:试计算第二个10s内V的平均变化率并比较与前者的大小?结果说明了什么?(1)4
(2)3
(3)2.1
(4)2.00113例4:已知函数f(x)=2x+1,g(x)=-2x,
分别计算在区间[-3,-1],[0,5]上f(x)及g(x)的平均变化率.思考:从本例中你发现一次函数y=kx+b在区间[m,n]上的平均变化率有什么特点?对于f(x):平均变化率为2;
对于g(x):平均变化率为-2;练一练,你是最棒的!3.试计算正弦函数y=sinx在区间 上的平均变化率.思考:你认为“正弦函数y=sinx的值在区间 上没有变化”说法对吗?定义探索:
A:同学们,练习3说明了什么?你对平均变化率又有怎样的理解?Answer:平均变化率量化一段曲线的陡峭程度是“粗糙不精确的”回顾反思: 通过今天的学习,你有哪些收获? 1.平均变化率的定义:2.平均变化率的意义:平均变化率是 曲线陡峭程度的“数量化”4.数学建模:将实际问题转化为数学模型来加以解决3.数形结合的思想思考题:向高度为H的水瓶内匀速注水,注满为止.如果水深h与注水时间t的函数的图象如图所示,那么这个图所对应的水瓶的形状是什么?作业布置: 1. P7 页的第2,4题结合第4题能否找到一种较精确地刻画曲线上某一点处的变化趋势的方法呢?若能,则如何用数学语言来刻画?2.研究性作业:再见谢谢大家3.已知函数f(x)=ax2在区间[1,2]上的平均变化率
为 ,则在区间[-2,-1]上的平均变化率为 ( )
A. B. C. D. 练一练,你是最棒的!4.试计算正弦函数y=sinx在区间 上的平均变化率.思考:你认为“正弦函数y=sinx的值在区间 上没有变化”说法对吗?A想一想 “生于忧患,死于安乐”
美国康乃尔大学的研究人员曾经做过这样一个实验:把一只青蛙扔进一锅热水中,青蛙一下子受到强烈刺激,于是奋足一跳,跳出锅外,成功保住了性命,而把另外一只青蛙放进一锅冷水中,然后慢慢加热,开始水是冰凉的,青蛙觉得很舒服,后来水温逐渐升高直至青蛙再难忍受才意识到危险;这时青蛙才努力想跳出热锅,但为时已晚,最后青蛙被煮死了。
树高:15米
树龄:1200年雨后春笋
高:15厘米
时间:两天问题与背景1:现有扬州市某年3月和4月某天日最高气温记载:温差15.1℃温差14.8℃问题与背景2:观察下面的气温曲线图(以3月18日作为第1天).问题1:由图象你能得到哪些信息?无形不直观21020300C(34, 33.4)T(℃)t(天)问题2:“气温陡增”这是一句生活用语,用数学方法如何量化陡峭程度呢?平均变化率的定义:一般地,函数 在区间 上的平均
变化率为:数学应用:1:某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率。解:(1)从出生到第3个月,婴儿体重平均变化率为:(2)平均变化率是曲线陡峭程度的“数量化”,或者说,曲线陡峭程度是平均变化率的“视觉化”关系如何?1.试求出CD、DE段上的平均变化率.2.你是怎样理解“—”号的?2030342102030A(1, 3.5)B(32, 18.6)0C(34, 33.4)T(℃)t(天)图4-1-1210D(37,27.7)E(40,27.1)例2:水经过虹吸管从容器甲中流向容器乙,t秒后容器甲中水的体积V(t)=5e-0.1t
(单位cm3),计算第一个10秒内V的平均变化率.解:在区间[0,10]上,体积的平均变化率为:数学应用:问题引申1:怎样解释结果中的“-”号?
问题引申2:若研究对象改为乙,此时平均变化率的正负号如何?
问题引申3:试计算第二个10s内V的平均变化率并比较与前者的大小?结果说明了什么?(1)4
(2)3
(3)2.1
(4)2.00113例4:已知函数f(x)=2x+1,g(x)=-2x,
分别计算在区间[-3,-1],[0,5]上f(x)及g(x)的平均变化率.思考:从本例中你发现一次函数y=kx+b在区间[m,n]上的平均变化率有什么特点?对于f(x):平均变化率为2;
对于g(x):平均变化率为-2;练一练,你是最棒的!3.试计算正弦函数y=sinx在区间 上的平均变化率.思考:你认为“正弦函数y=sinx的值在区间 上没有变化”说法对吗?定义探索:
A:同学们,练习3说明了什么?你对平均变化率又有怎样的理解?Answer:平均变化率量化一段曲线的陡峭程度是“粗糙不精确的”回顾反思: 通过今天的学习,你有哪些收获? 1.平均变化率的定义:2.平均变化率的意义:平均变化率是 曲线陡峭程度的“数量化”4.数学建模:将实际问题转化为数学模型来加以解决3.数形结合的思想思考题:向高度为H的水瓶内匀速注水,注满为止.如果水深h与注水时间t的函数的图象如图所示,那么这个图所对应的水瓶的形状是什么?作业布置: 1. P7 页的第2,4题结合第4题能否找到一种较精确地刻画曲线上某一点处的变化趋势的方法呢?若能,则如何用数学语言来刻画?2.研究性作业:再见谢谢大家3.已知函数f(x)=ax2在区间[1,2]上的平均变化率
为 ,则在区间[-2,-1]上的平均变化率为 ( )
A. B. C. D. 练一练,你是最棒的!4.试计算正弦函数y=sinx在区间 上的平均变化率.思考:你认为“正弦函数y=sinx的值在区间 上没有变化”说法对吗?A想一想 “生于忧患,死于安乐”
美国康乃尔大学的研究人员曾经做过这样一个实验:把一只青蛙扔进一锅热水中,青蛙一下子受到强烈刺激,于是奋足一跳,跳出锅外,成功保住了性命,而把另外一只青蛙放进一锅冷水中,然后慢慢加热,开始水是冰凉的,青蛙觉得很舒服,后来水温逐渐升高直至青蛙再难忍受才意识到危险;这时青蛙才努力想跳出热锅,但为时已晚,最后青蛙被煮死了。
