指数函数
图片预览


文档简介
(共21张PPT)
3.1.2
指
数
函
数
指
数
函
数
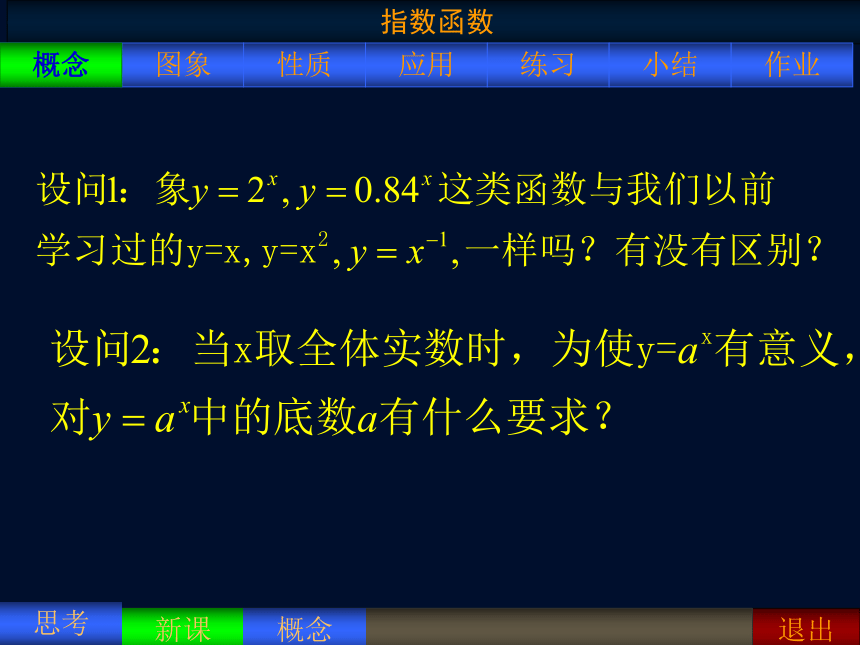
问题2
新课
思考
概念
概念
思考
概念
概念
新课
1.某种细胞分裂时,由1个分裂成两 个,两个分裂成4个……,一个这样的细胞分裂x次后,得到的细胞个数y与x的函数关系是 。
2. 某种放射性物质不断变化为其它物质,每经过 1 年剩留的这种物质是原来的84﹪。问这种物质的剩留量经过x年后还剩下多少?(设原来的质量为1)
问题2
新课
概念
概念
思考
概念
一般地,函数
叫做
指数函数,
其中 x 是自变量,
函数的定义域是R。
问题1
问题2
概念
图象
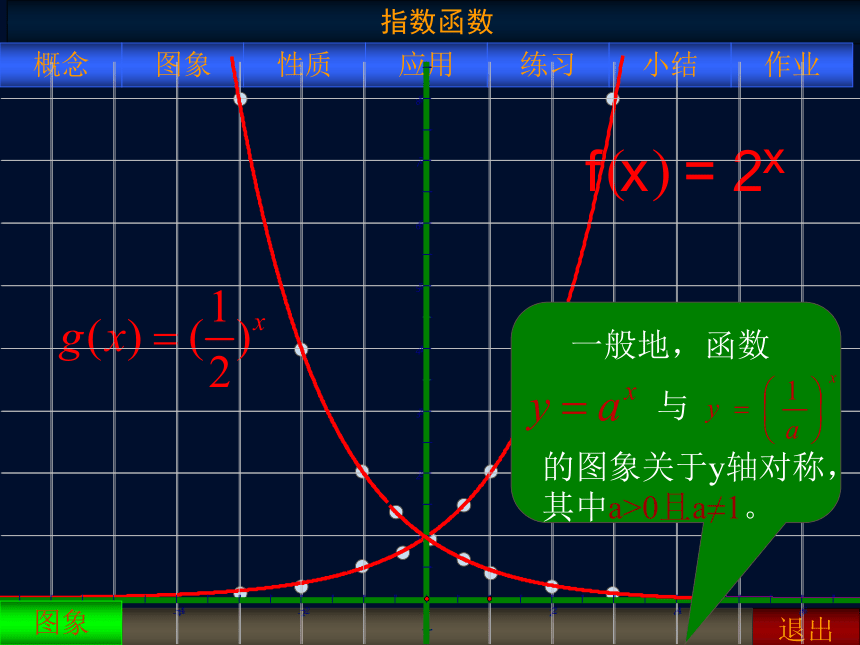
画出函数 与 的图象。
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
…
3
2
1
0.5
0
-0.5
-1
-2
-3
…
x
列表
图象
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
f
x
(
)
=
2
x
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
一般地,函数
与
的图象关于y轴对称,其中a>0且a≠1。
图象
图 象
性 质
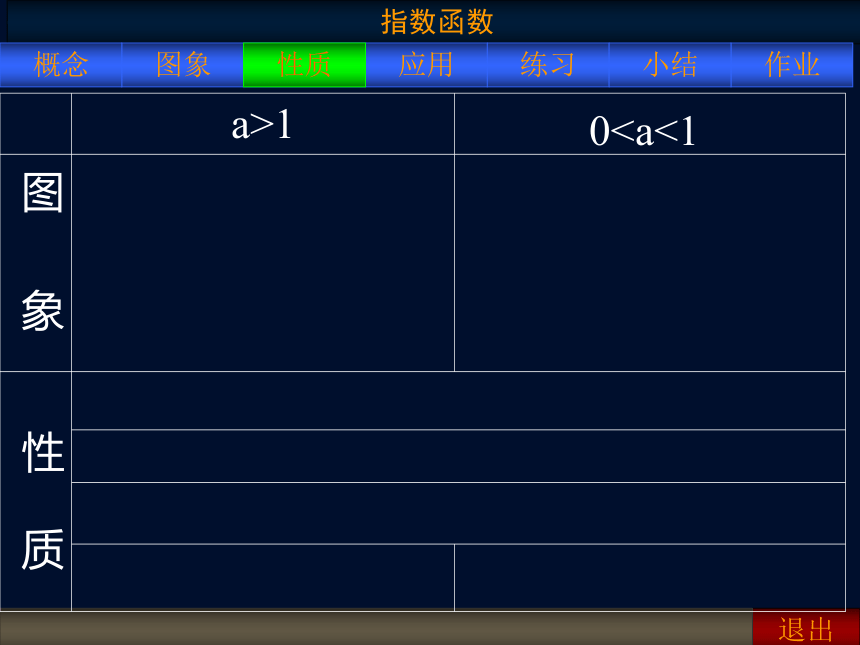
a>1
0性质
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
性质
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
当 x < 0 时,y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,y < 1。
性质
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
当 x < 0 时,y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,y < 1。
性质
应用
例1
练习
练习1
练习2
2.练习:
(1,+ )
(0, + )
[1, + )
(0,1]
(-1/2,0)
练习
练习2
练习1
小结
一般地,函数
叫做
指数函数,
其中 x 是自变量。
函数的定义域是R。
概念
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
概念
图象与性质
小结
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
当 x < 0 时,y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,y < 1。
概念
图象与性质
小结
作业
课本P93:习题 B:2、3.
思考题:A先生从今天开始每天给你10万元,而你第一天给A先生1元,第二天给A先生2元,第三天给A先生4元,第四天给A先生8元……
(1)A先生要和你签订15天的合同,你同意签订这个合同吗?
(2)A先生要和你签订30天的合同,你同意签订这个合同吗?
再见!
3.1.2
指
数
函
数
指
数
函
数
问题2
新课
思考
概念
概念
思考
概念
概念
新课
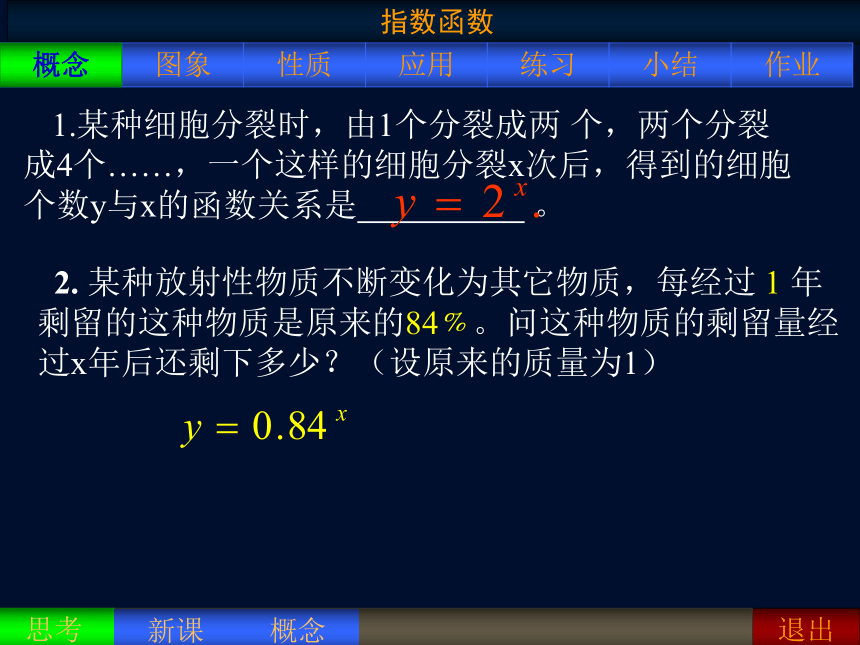
1.某种细胞分裂时,由1个分裂成两 个,两个分裂成4个……,一个这样的细胞分裂x次后,得到的细胞个数y与x的函数关系是 。
2. 某种放射性物质不断变化为其它物质,每经过 1 年剩留的这种物质是原来的84﹪。问这种物质的剩留量经过x年后还剩下多少?(设原来的质量为1)
问题2
新课
概念
概念
思考
概念
一般地,函数
叫做
指数函数,
其中 x 是自变量,
函数的定义域是R。
问题1
问题2
概念
图象
画出函数 与 的图象。
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
…
3
2
1
0.5
0
-0.5
-1
-2
-3
…
x
列表
图象
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
f
x
(
)
=
2
x
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
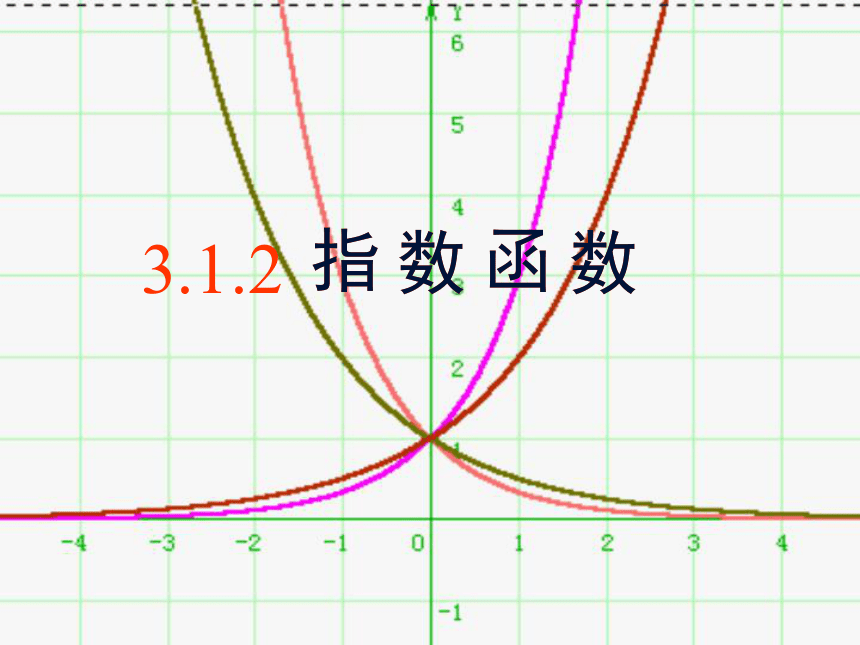
一般地,函数
与
的图象关于y轴对称,其中a>0且a≠1。
图象
图 象
性 质
a>1
0
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
性质
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
当 x < 0 时,y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,y < 1。
性质
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
当 x < 0 时,y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,y < 1。
性质
应用
例1
练习
练习1
练习2
2.练习:
(1,+ )
(0, + )
[1, + )
(0,1]
(-1/2,0)
练习
练习2
练习1
小结
一般地,函数
叫做
指数函数,
其中 x 是自变量。
函数的定义域是R。
概念
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
概念
图象与性质
小结
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
必过 点:
在 R 上是
在 R 上是
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
当 x < 0 时,y < 1;
当 x > 0 时,y > 1.
当 x < 0 时,y > 1;
当 x > 0 时,y < 1。
概念
图象与性质
小结
作业
课本P93:习题 B:2、3.
思考题:A先生从今天开始每天给你10万元,而你第一天给A先生1元,第二天给A先生2元,第三天给A先生4元,第四天给A先生8元……
(1)A先生要和你签订15天的合同,你同意签订这个合同吗?
(2)A先生要和你签订30天的合同,你同意签订这个合同吗?
再见!
