复数的几何意义
图片预览



文档简介
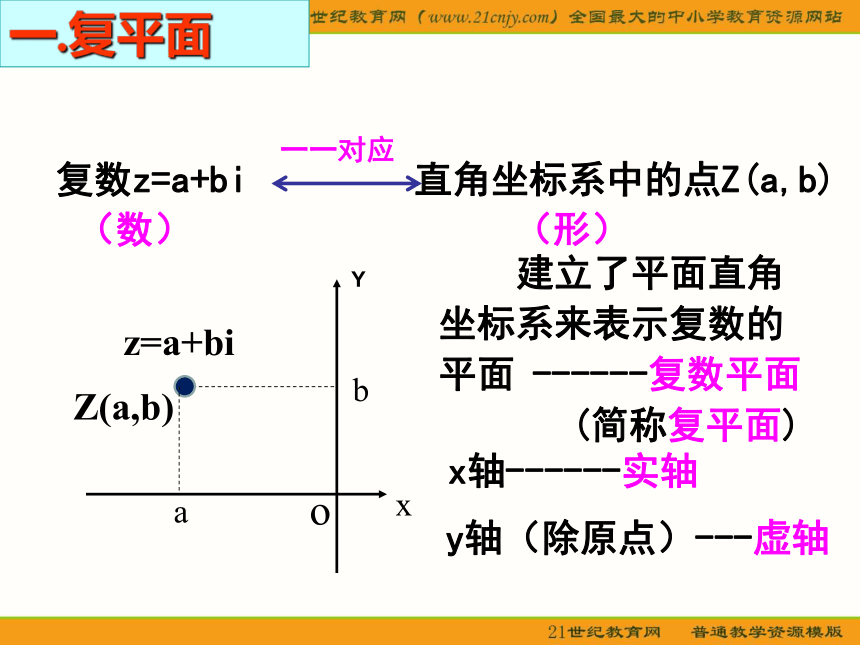
课件15张PPT。3.1 复数的概念Z=a+bi(a, b∈R)实部!虚部!复数的代数形式:一个复数由有序实数对 (a,b)确定实数可以用数轴上的点来表示。实数 数轴上的点 一一对应 (数)(形)类比实数的表示,可以用直角坐标系中的点的点来表示复数一.复平面x轴------实轴y轴(除原点)---虚轴例1、在复平面内表示下列复数
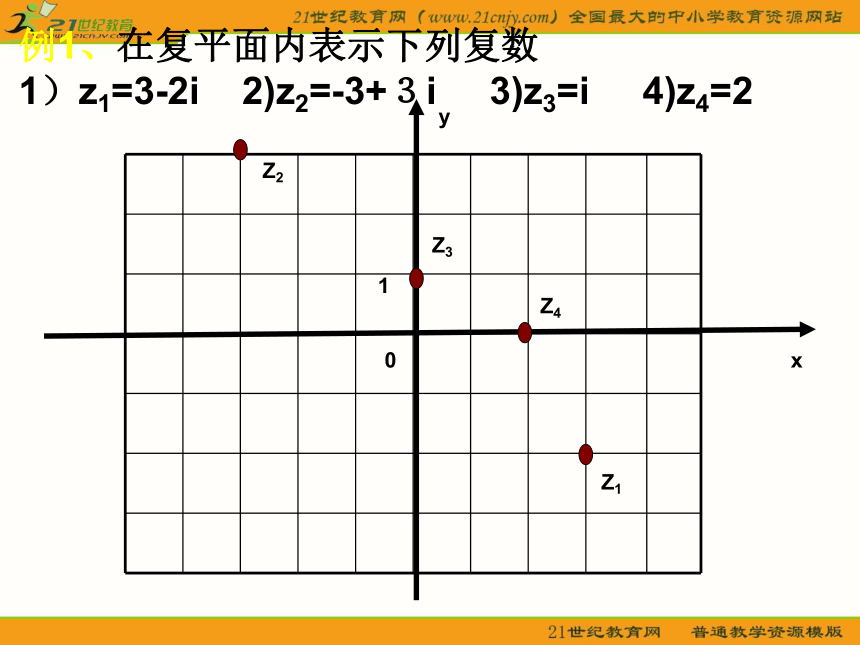
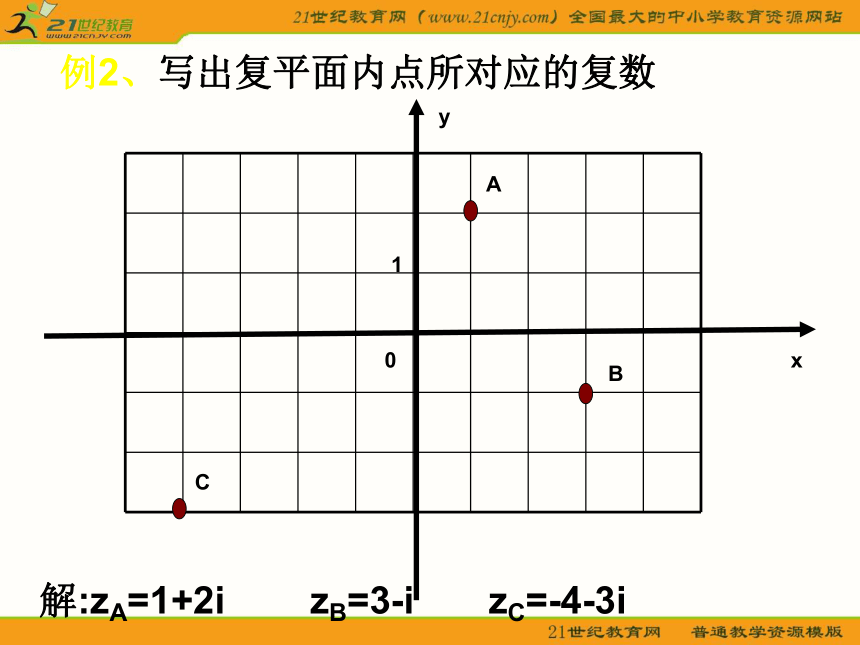
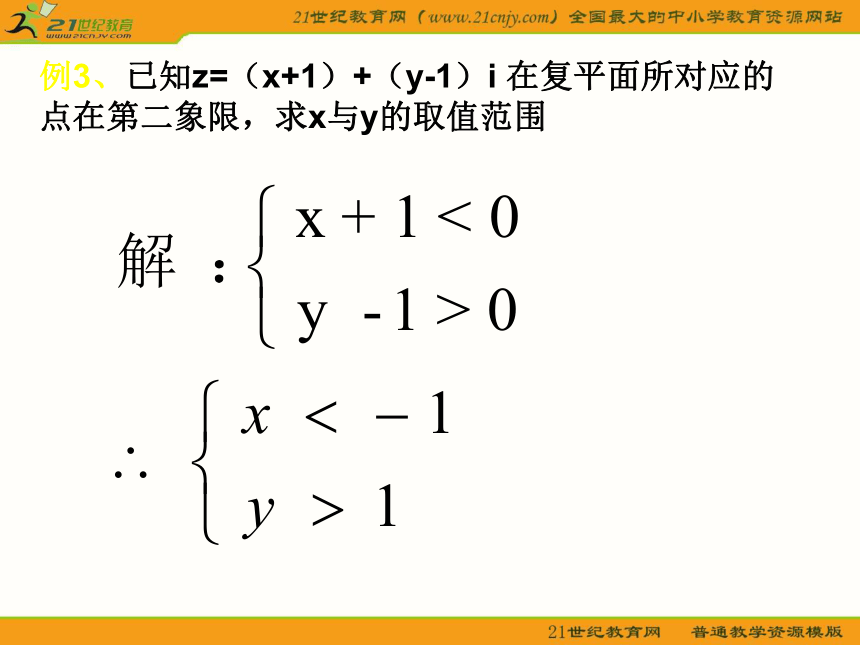
1)z1=3-2i 2)z2=-3+3i 3)z3=i 4)z4=2x0yZ1Z2Z3Z41例2、写出复平面内点所对应的复数0yxABC1解:zA=1+2i zB=3-i zC=-4-3i例3、已知z=(x+1)+(y-1)i 在复平面所对应的点在第二象限,求x与y的取值范围例4、已知复数z=(m2+m-2)-mi在复平面内所对应的点位于第四象限,求实数m的取值范围一种重要的数学思想:数形结合思想二、复数的向量表示xyobaZ(a,b)z=a+bi三、复数的摸向量 的模叫做复数z=a+bi的模,记做
复数的模的几何意义:
复数z=a+bi在复平面所对应的点Z(a,b)到原点的距离
例4、已知复数z 1=3+2i,z2=-2+4i,比较这两个复数模的大小解:因为复数的模是实数,所以可以比较大小练习:已知复数 的模为5,求k的值总结:1、复平面及其相关定义2、复数的向量表示3、复数的模及其几何意义练习思考:(1)满足 的z值有几个?
(2)满足 复数z对应的点在复平面上将构成怎样的图形?谢 谢 指 教
1)z1=3-2i 2)z2=-3+3i 3)z3=i 4)z4=2x0yZ1Z2Z3Z41例2、写出复平面内点所对应的复数0yxABC1解:zA=1+2i zB=3-i zC=-4-3i例3、已知z=(x+1)+(y-1)i 在复平面所对应的点在第二象限,求x与y的取值范围例4、已知复数z=(m2+m-2)-mi在复平面内所对应的点位于第四象限,求实数m的取值范围一种重要的数学思想:数形结合思想二、复数的向量表示xyobaZ(a,b)z=a+bi三、复数的摸向量 的模叫做复数z=a+bi的模,记做
复数的模的几何意义:
复数z=a+bi在复平面所对应的点Z(a,b)到原点的距离
例4、已知复数z 1=3+2i,z2=-2+4i,比较这两个复数模的大小解:因为复数的模是实数,所以可以比较大小练习:已知复数 的模为5,求k的值总结:1、复平面及其相关定义2、复数的向量表示3、复数的模及其几何意义练习思考:(1)满足 的z值有几个?
(2)满足 复数z对应的点在复平面上将构成怎样的图形?谢 谢 指 教
