函数的最值与导数
图片预览


文档简介
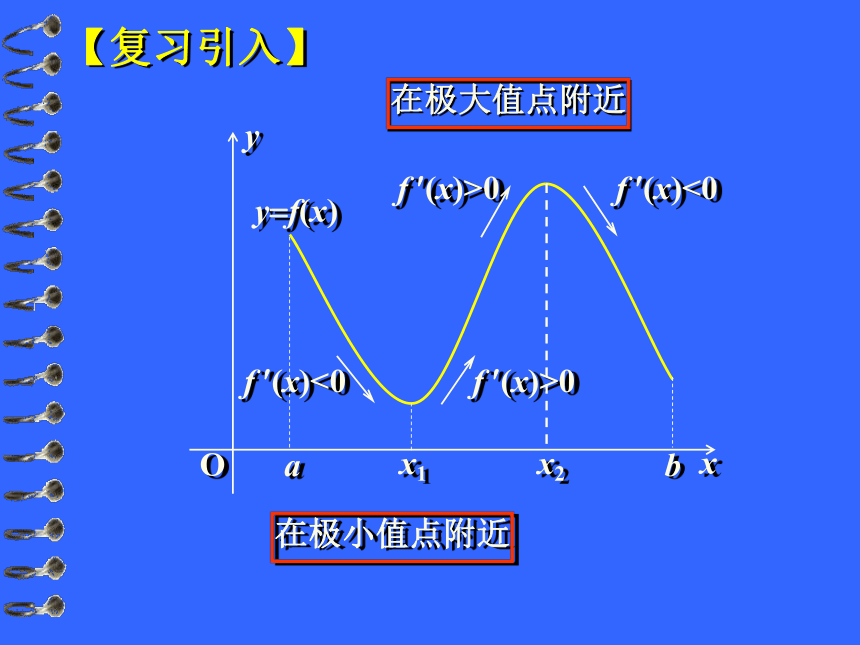
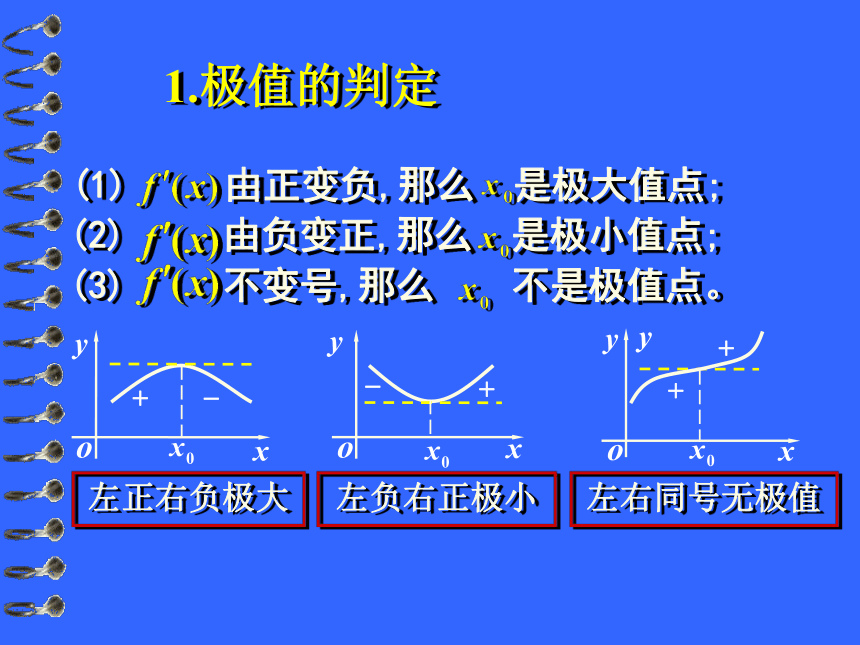
课件10张PPT。函数的最值与导数 f ?(x)<0 f ?(x)>0 f ?(x)>0 f ?(x)<0在极大值点附近在极小值点附近【复习引入】左正右负极大左负右正极小左右同号无极值(2) 由负变正,那么 是极小值点;(3) 不变号,那么 不是极值点。(1) 由正变负,那么 是极大值点;1.极值的判定(1) 确定函数的定义域 (一般可省) ;2.求可导函数 f (x) 的极值点和极值的步骤:(2) 求出导数 f ′(x); (3) 令f ′(x)=0,解方程; 列表:把定义域划分为部分区间,
考察每个部分区间内 f ′(x) 的符号,
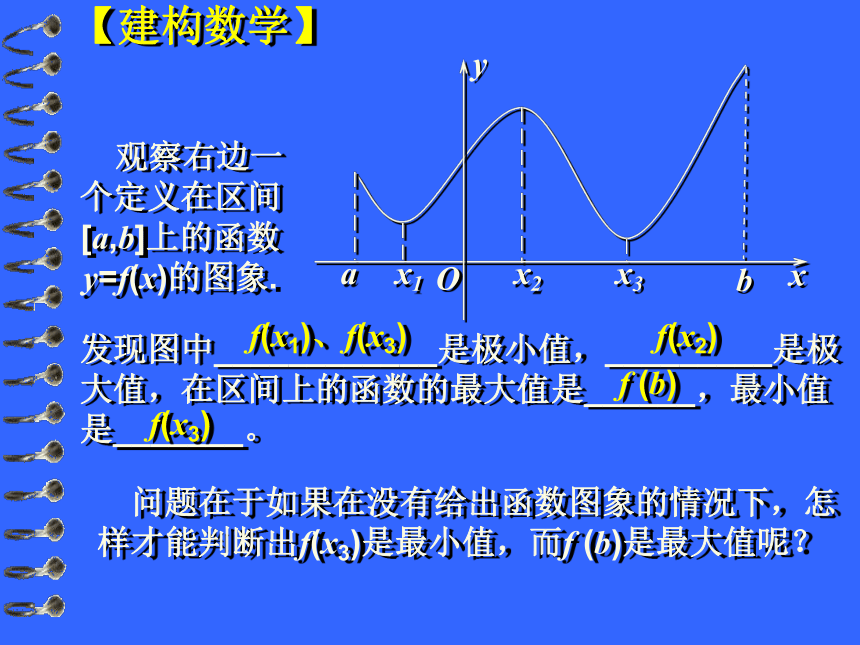
判断f (x)的单调性从而确定极值点;(5)下结论,写出极值。 观察右边一个定义在区间[a,b]上的函数y=f(x)的图象.发现图中____________是极小值,_________是极大值,在区间上的函数的最大值是______,最小值是_______。f(x1)、f(x3)f(x2)f (b)f(x3) 问题在于如果在没有给出函数图象的情况下,怎 样才能判断出f(x3)是最小值,而f (b)是最大值呢? 【建构数学】设函数f(x)在[a,b]上有定义,则求f(x)
在[a,b]上的最大值与最小值的步骤如下:①求y=f(x)在(a,b)内的极值(极大值与极小值); ②将函数y=f(x)的各极值与f(a)、f(b)作比较,其中最大的一个为最大值,最小的一个为最小值。注意1) 函数的最值概念是全局性的2) 函数的最大值(最小值)唯一3) 函数的最大值大于等于最小值4) 函数的最值可在端点处取得例1:求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值。解:令 ,解得x=-1,0,1。当x变化时, 的变化情况如下表:从上表可知,最大值是13,最小值是4。1345↗4↘130-0+0-2(1,2)1(0,1)0(-1,0)-1(-2,-1)-2【数学运用】+↘↗例2:求函数 y = x3 + 3 x2-9x在[-4 , 4 ]上
的最大值和最小值。函数在[-4 , 4 ]上的最大值为 f (4) =76,最小值为 f (1)=-5 。思考:设 ,函数 的最
大值为1,最小值为 ,求常数 a,b。 b=1小 结
考察每个部分区间内 f ′(x) 的符号,
判断f (x)的单调性从而确定极值点;(5)下结论,写出极值。 观察右边一个定义在区间[a,b]上的函数y=f(x)的图象.发现图中____________是极小值,_________是极大值,在区间上的函数的最大值是______,最小值是_______。f(x1)、f(x3)f(x2)f (b)f(x3) 问题在于如果在没有给出函数图象的情况下,怎 样才能判断出f(x3)是最小值,而f (b)是最大值呢? 【建构数学】设函数f(x)在[a,b]上有定义,则求f(x)
在[a,b]上的最大值与最小值的步骤如下:①求y=f(x)在(a,b)内的极值(极大值与极小值); ②将函数y=f(x)的各极值与f(a)、f(b)作比较,其中最大的一个为最大值,最小的一个为最小值。注意1) 函数的最值概念是全局性的2) 函数的最大值(最小值)唯一3) 函数的最大值大于等于最小值4) 函数的最值可在端点处取得例1:求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值。解:令 ,解得x=-1,0,1。当x变化时, 的变化情况如下表:从上表可知,最大值是13,最小值是4。1345↗4↘130-0+0-2(1,2)1(0,1)0(-1,0)-1(-2,-1)-2【数学运用】+↘↗例2:求函数 y = x3 + 3 x2-9x在[-4 , 4 ]上
的最大值和最小值。函数在[-4 , 4 ]上的最大值为 f (4) =76,最小值为 f (1)=-5 。思考:设 ,函数 的最
大值为1,最小值为 ,求常数 a,b。 b=1小 结
