指数函数的图象和性质

课件18张PPT。指数函数的图象和性质第一课时 我是电脑病毒，在传播
时我可以由一个复制成二个，
二个复制成四个，……，我
复制x次后，得到的病毒个数
y与x有怎样的函数关系？
如果做不出，可要小心你
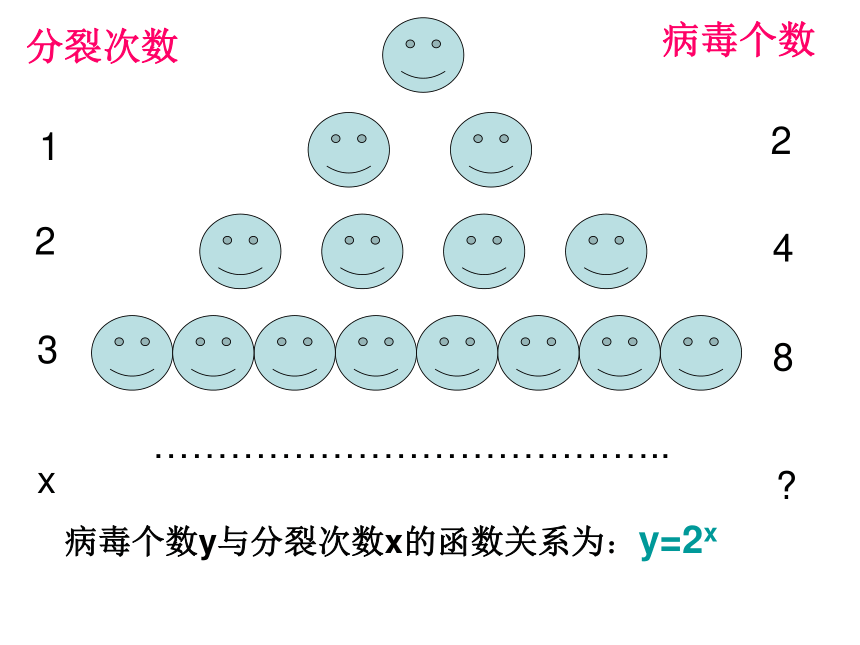
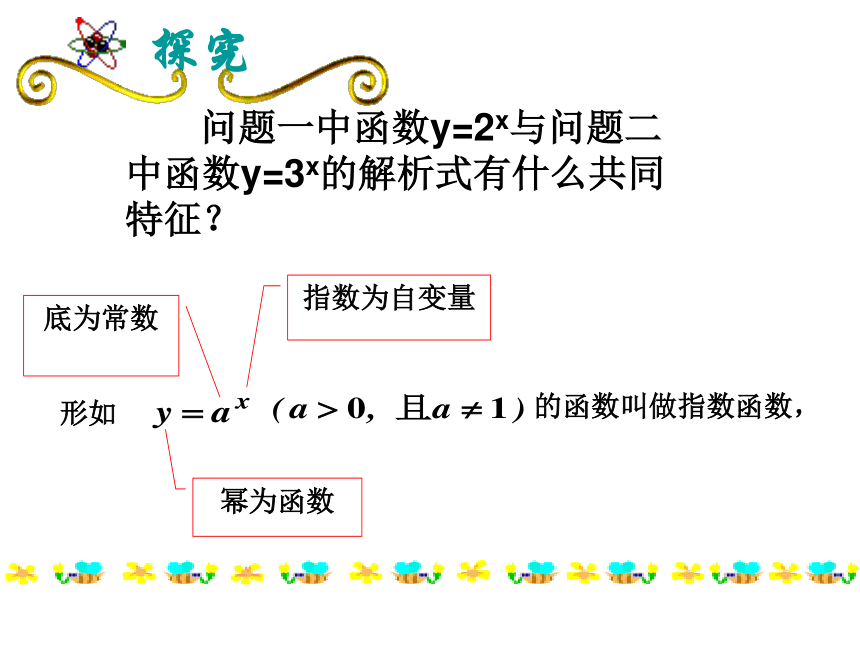
的电脑哦！问题一分裂次数病毒个数123248…………………………………..x?病毒个数y与分裂次数x的函数关系为：y=2x问题二 铀核裂变能产生巨大的能量，它的裂变方式称为链式反应，假定1个中子击打1个铀核，此中子被吸收产生能量并释放出3个中子，这3个中子又打中另外3个铀核产生3倍的能量并释放出9个中子，这9个中子又击中9个铀核……这样的击打进行了x次后释放出的中子数y与x的关系是：y=3x（x∈N*）探究 问题一中函数y=2x与问题二中函数y=3x的解析式有什么共同特征？
指数为自变量幂为函数底为常数函数叫做指数函数，为自变量，定义域为 。其中指数函数定义(1)如果a<0, 比如y=(-4)x，这时对于x=1／4,x=1／2等，在实数范围内函数值不存在；
(2)如果a=0，当x>0时, y=0;当x≤0时，y无意义。
(3)如果a=1，y=1，是个常值函数，没有研究的必要；
(4)如果01即a>0且a≠1，x可以是任意实数。
* 因为指数概念已经扩充到整个实数范围，所以在a>0且a≠1的前提下，x可以是任意实数,即指数函数的定义域为R。下列函数中，哪些是指数函数？
我是我不是?怎样得到指数函数图像?
指数函数图像的特点?
通过图像，你能发现指数函数的哪 些性质?思考分组画出下列四个函数的图象：
(1)y=2x (2)y=(1／2)x
(3)y=3x (4)y=(1／3)x 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(010 0 时，y > 1.
当 x < 0 时，. 0< y < 1
当 x < 0 时，y > 1；
当 x > 0 时， 0< y < 1。底互为倒数的两个函数图像关于y轴对称 在第一象限沿箭头方向底增大深入探究 你还能发现指数函数图象和底数的关系吗？例题讲解 例1：已知指数函数f(x)=ax(a>0且a≠1)的
图象经过点（2，16），求f(0),f(1),f(-3)的值。解：∵ f(x)的图象过点（2，16），∴ f(2)=16即a2=16,
又a>0且a≠1∴ a=4 ,f(x)=4x.∴ f(0)=40=1,f(1)=41=4,f(-3)=4-3=1／64.例2：某种放射性物质不断变化为其他物质，每经过一年剩留的这种物质变为原来的84%。画出这种物质的剩留量随时间变化的图象，并从图象上求出经过多少年，剩留量是原来的一半（保留一个有效数字）？解：设这种物质最初的质量是1，经过x年后，剩留量是y。经过1年，剩留量经过2年，剩留量…………一般地，经过x年，剩留量
根据这个函数关系可以列表如下： 答：约经过4年，剩留量是原来的一半。课堂练习1、求下列函数的定义域：
2、函数y=a2x-3+3恒过定点 。3、如图是指数函数①，②③，④的图象，则a,b,c,d的大小关系是（　　）
A．
B．C．
D．B（3／2，4）通过本节课的学习，你学到了哪些知识？
你又掌握了哪些学习数学方法？
你能将指数函数的学习与实际生活联系起来吗？ 课堂小结作业必做题 p59:A组5,6
选做题 p60:B组3.想一想 A先生从今天开始每天给你10万元,而你承担如下任务:第一天给A先生1元,第二天给A先生2元,,第三天给A先生4元,第四天给A先生8元,依次下去…那么,A先生要和你签定15天的合同,你同意吗?又A先生要和你签定30天的合同,你能签这个合同吗? 今天我们所学的性质是由观察图像得到的，那么这些性质能否通过推理的方法得到呢？思考双峰一中 吴科文谢谢大家