演绎推理
图片预览







文档简介
课件20张PPT。演 绎 推 理小明是一名高二年级的学生,17岁,迷恋上网络,沉迷于虚拟的世界当中。由于每月的零花钱不够用,便向亲戚要钱,但这仍然满足不了需求,于是就产生了歹念,强行向路人抢取钱财。在被抓住后小明却说我是未成年人而且就抢了50元,这应该不会很严重吧???
《刑法》规定年龄起点为14周岁以上,以非法占有为目的,使用暴力、胁迫或其他方法,强行劫取公私财物的行为,无论数额大小,均是犯抢劫罪。 请同学们当回大法官:
如果你是法官,你会如何判决呢?小明到底是不是犯了抢劫罪呢?你的依据是什么?
因为《刑法》规定年龄14周岁以上, …强行劫取公私财物的行为,无论数额大小,均是犯抢劫罪。
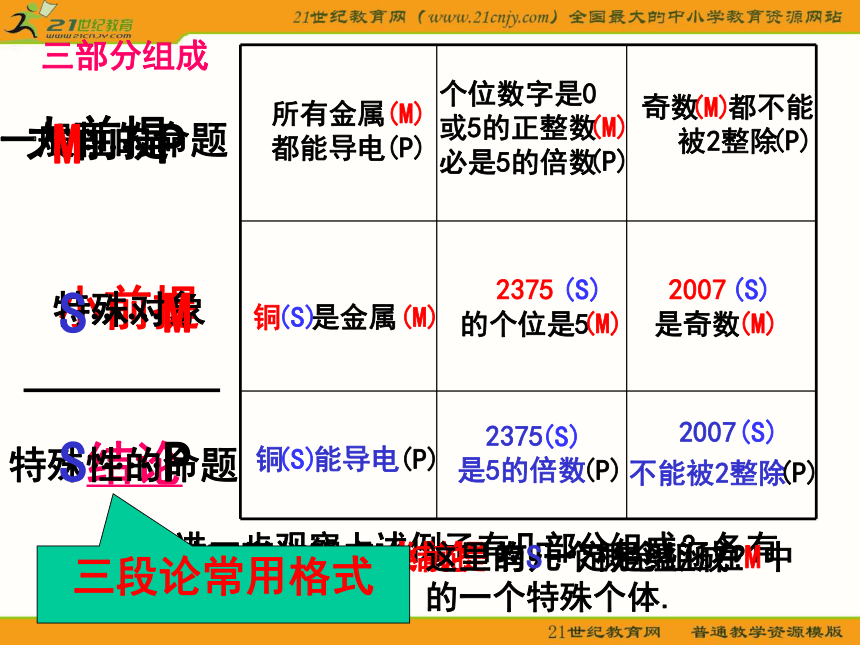
小明犯了抢劫罪。 而小明超过14周岁,强行向路人抢取钱财50元。 观察与思考1.所有的金属都能导电, 2.个位数字是0或5的正整数必是5的倍数, 3.所有奇数都不能被2整除, 所以,铜能够导电.铜是金属, 所以,2375是5的倍数.2375的个位是5,2007是奇数,所以2007不能被2整除.观察上述例子有什么共同特点?1,由一般到特殊的推理,2007不能被2整除2375是5的倍数铜能导电我们把这种推理称为演绎推理.铜是金属2007是奇数2375的个位是5进一步观察上述例子有几部分组成?各有什么特点?大前提小前提结论一般性的命题特殊性的命题特殊对象2007
不能被2整除铜 能导电奇数 都不能被2整除2007
是奇数个位数字是0或5的正整数必是5的倍数
铜 是金属(S)(M)(P)所有金属
都能导电2375 的个位是52375
是5的倍数(P)(P)(P)(P)(P)(M)(M)(M)(M)(M)(S)(S)(S)(S)(S)请同学们观察 有几个概念组成?
前提大小结论M……PS……MS……P三段论常用格式这里的S一定是蕴涵在M中的一个特殊个体.三部分组成“三段论”是演绎推理的一般模式,包括:
(1)大前提——已知的一般原理;
(2)小前提——所研究的特殊情况;
(3)结 论——根据一般原理,对特殊
情况做出的判断。
2、三段论例1:把下列推理恢复成完全的三段论:
(1)等边三角形内角和是180° 。
大前提:所有三角形内角和是180°,
(2) 是有理数。大前提:所有的循环小数都是有理数, 小前提: 是循环小数,小前提:等边三角形是三角形,结论:所以等边三角形内角和是180°。结论: 所以 是有理数。解:解:错因:大前提是错误的,所以结论是错误的。
① 因为指数函数 是增函数,
而 是指数函数,
所以 是增函数。 演绎推理的结论一定正确吗? 判断下列推理是否正确,如果错误,请指出错因.②整数是自然数,-3是整数,-3是自然数;③无理数是无限小数,是无限小数,是无理数.错因:大前提错误错因:推理形式错误2007不能被2整除2375是5的倍数铜能导电大前提小前提结论在演绎推理中,只要前提和推理形式是正确的,结论必定正确。奇数都不能被2整除铜是金属2375的个位
是5④例2如图,D,E,F分别是BC,CA,AB上的点, ∠BFD=∠A,DE∥BA, 求证:ED=AF.}四边形AFDE是平行四边形ED=AF∠BFD=∠ADF∥EADE∥BA证明:ABCDEF例2如图,D,E,F分别是BC,CA,AB上的点, ∠BFD=∠A,DE∥BA, 求证:ED=AF.证:(1)同位角相等,两直线平行,
∠BFD与∠A是同位角且 ∠BFD=∠A,
所以,DF∥EA.
(2)两组对边分别平行的四边形是平行四边形
DF∥EA 且DE∥BA
所以,四边形AFDE是平行四边形.
(3)平行四边形的对边相等,
ED和AF为平行四边形的对边.
所以,ED=AF. 大前提大前提大前提小前提小前提
小前提
结论结论结论练习:已知a,b,m均为正实数,b﹤a, 求证:证: b﹤a
m﹥0}mb﹤maab+mb﹤ab+mab(a+m) ﹤a(b+m)a(a+m) ﹥0}又 通过以上的学习我们思考一下,演绎推理有哪些特点?1.由一般推演到特殊的推理过程;2.只要前提正确,推理形式正确,结论一定正确;3.它可以作为数学证明工具;4.但演绎推理是一种收敛性思维方式,它较少创造性.演绎推理特点
常用形式——三段论
证明问题
合情推理与演绎推理的区别(难点)(重点)(重点)四、小结 演绎推理与合情推理的区别:由特殊到一般的推理。由特殊到特殊的推理。
由一般到特殊的推理。
结论不一定正确,有待进一步证明。 在前提和推理形式都正确的前提下,得到的结论一定正确。 1、教材71页第5题
2、找一个你感兴趣的数学定义、公式或定理,探究它的来源,你也可以通过翻阅书籍、上网查找资料寻求依据。五、作业1掌握以下知识:
1、什么是演绎推理?
2、什么是三段论?
3、合情推理与演绎推理有哪些区别?
4、你能举出一些在生活和学习中有关演绎
推理的例子吗?课后作业2:在数列{an}中,
试猜想这个数列的通项公式;
并用演绎推理证明你的猜想。思考题:欢迎各位专家和同仁莅临指导!谢谢
《刑法》规定年龄起点为14周岁以上,以非法占有为目的,使用暴力、胁迫或其他方法,强行劫取公私财物的行为,无论数额大小,均是犯抢劫罪。 请同学们当回大法官:
如果你是法官,你会如何判决呢?小明到底是不是犯了抢劫罪呢?你的依据是什么?
因为《刑法》规定年龄14周岁以上, …强行劫取公私财物的行为,无论数额大小,均是犯抢劫罪。
小明犯了抢劫罪。 而小明超过14周岁,强行向路人抢取钱财50元。 观察与思考1.所有的金属都能导电, 2.个位数字是0或5的正整数必是5的倍数, 3.所有奇数都不能被2整除, 所以,铜能够导电.铜是金属, 所以,2375是5的倍数.2375的个位是5,2007是奇数,所以2007不能被2整除.观察上述例子有什么共同特点?1,由一般到特殊的推理,2007不能被2整除2375是5的倍数铜能导电我们把这种推理称为演绎推理.铜是金属2007是奇数2375的个位是5进一步观察上述例子有几部分组成?各有什么特点?大前提小前提结论一般性的命题特殊性的命题特殊对象2007
不能被2整除铜 能导电奇数 都不能被2整除2007
是奇数个位数字是0或5的正整数必是5的倍数
铜 是金属(S)(M)(P)所有金属
都能导电2375 的个位是52375
是5的倍数(P)(P)(P)(P)(P)(M)(M)(M)(M)(M)(S)(S)(S)(S)(S)请同学们观察 有几个概念组成?
前提大小结论M……PS……MS……P三段论常用格式这里的S一定是蕴涵在M中的一个特殊个体.三部分组成“三段论”是演绎推理的一般模式,包括:
(1)大前提——已知的一般原理;
(2)小前提——所研究的特殊情况;
(3)结 论——根据一般原理,对特殊
情况做出的判断。
2、三段论例1:把下列推理恢复成完全的三段论:
(1)等边三角形内角和是180° 。
大前提:所有三角形内角和是180°,
(2) 是有理数。大前提:所有的循环小数都是有理数, 小前提: 是循环小数,小前提:等边三角形是三角形,结论:所以等边三角形内角和是180°。结论: 所以 是有理数。解:解:错因:大前提是错误的,所以结论是错误的。
① 因为指数函数 是增函数,
而 是指数函数,
所以 是增函数。 演绎推理的结论一定正确吗? 判断下列推理是否正确,如果错误,请指出错因.②整数是自然数,-3是整数,-3是自然数;③无理数是无限小数,是无限小数,是无理数.错因:大前提错误错因:推理形式错误2007不能被2整除2375是5的倍数铜能导电大前提小前提结论在演绎推理中,只要前提和推理形式是正确的,结论必定正确。奇数都不能被2整除铜是金属2375的个位
是5④例2如图,D,E,F分别是BC,CA,AB上的点, ∠BFD=∠A,DE∥BA, 求证:ED=AF.}四边形AFDE是平行四边形ED=AF∠BFD=∠ADF∥EADE∥BA证明:ABCDEF例2如图,D,E,F分别是BC,CA,AB上的点, ∠BFD=∠A,DE∥BA, 求证:ED=AF.证:(1)同位角相等,两直线平行,
∠BFD与∠A是同位角且 ∠BFD=∠A,
所以,DF∥EA.
(2)两组对边分别平行的四边形是平行四边形
DF∥EA 且DE∥BA
所以,四边形AFDE是平行四边形.
(3)平行四边形的对边相等,
ED和AF为平行四边形的对边.
所以,ED=AF. 大前提大前提大前提小前提小前提
小前提
结论结论结论练习:已知a,b,m均为正实数,b﹤a, 求证:证: b﹤a
m﹥0}mb﹤maab+mb﹤ab+mab(a+m) ﹤a(b+m)a(a+m) ﹥0}又 通过以上的学习我们思考一下,演绎推理有哪些特点?1.由一般推演到特殊的推理过程;2.只要前提正确,推理形式正确,结论一定正确;3.它可以作为数学证明工具;4.但演绎推理是一种收敛性思维方式,它较少创造性.演绎推理特点
常用形式——三段论
证明问题
合情推理与演绎推理的区别(难点)(重点)(重点)四、小结 演绎推理与合情推理的区别:由特殊到一般的推理。由特殊到特殊的推理。
由一般到特殊的推理。
结论不一定正确,有待进一步证明。 在前提和推理形式都正确的前提下,得到的结论一定正确。 1、教材71页第5题
2、找一个你感兴趣的数学定义、公式或定理,探究它的来源,你也可以通过翻阅书籍、上网查找资料寻求依据。五、作业1掌握以下知识:
1、什么是演绎推理?
2、什么是三段论?
3、合情推理与演绎推理有哪些区别?
4、你能举出一些在生活和学习中有关演绎
推理的例子吗?课后作业2:在数列{an}中,
试猜想这个数列的通项公式;
并用演绎推理证明你的猜想。思考题:欢迎各位专家和同仁莅临指导!谢谢
