新课标人教B版必修1第二章函数函数的单调性
文档属性
| 名称 | 新课标人教B版必修1第二章函数函数的单调性 |

|
|
| 格式 | rar | ||
| 文件大小 | 390.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-22 00:00:00 | ||
图片预览




文档简介
课件13张PPT。
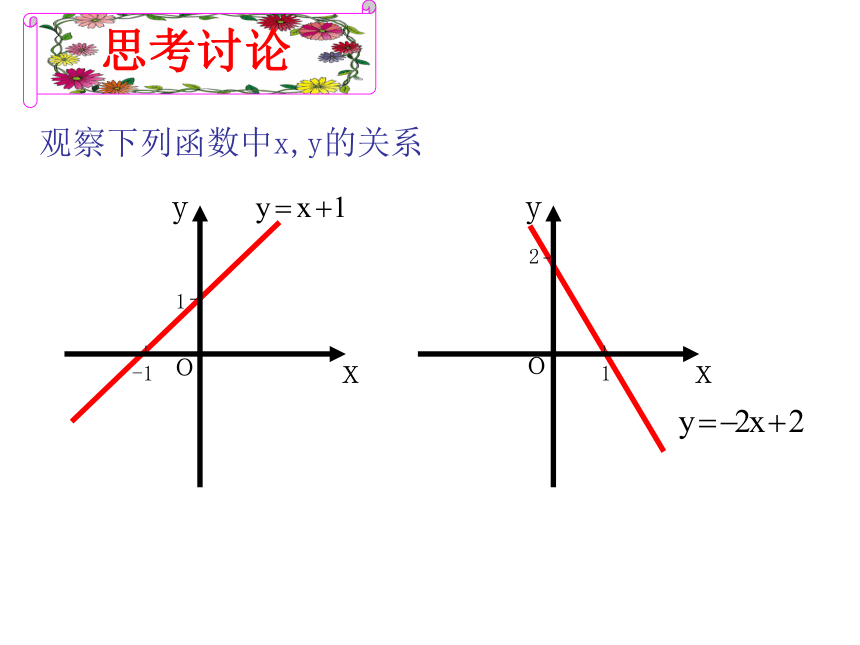
函数的单调性观察下列函数中x,y的关系思考讨论在 上,
y随x的增大而减小在 上,
y随x的增大而减小 函数f (x)在给定区间上为增函数。如何用x与 f(x)来表述上升的图象?如何用x与 f(x)来表述下降的图象? 函数f (x)在给定区间上为减函数。y=f(x)yx0x1x2f(x1)f(x2)
设函数y=f(x)的定义域为I, 如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2,当x1 如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2,当x1f(x2),那么就说函数f(x)在区间D上是减函数注意:(1)函数的单调性也叫函数的增减性;(2)函数的单调性是对某个区间而言的,它是个局部概
念。这个区间是定义域的子集。(3)单调区间:针对自变量 x 而言的。
若函数在此区间上是增函数,则为单调递增区间;
若函数在此区间上是减函数,则为单调递减区间.例1 如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,函数y=f(x)是增函数还是减函数. 解:函数f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中f(x)在区间[-5,-2),[1,3)上是减函数,
在区间[-2,1),[3,5]上是增函数.例题赏析(1)根据函数图像,指出函数在哪些区间上是减函数.(2)根据函数图像,指出函数在哪些区间上是增函数. 注意!用逗号间隔开演练反馈例2 证明函数 在R上是增函数.证明:设 是R上的任意两个实数,且 则:在R上是增函数. 例题赏析【判断函数单调性的步骤】1、设任意x1,x2属于给定区间,且x1 f(x1)-f(x2) >0,则f(x)为减函数.(通分、因式分解、配方)(取值)(作差化简)(定号)(结论) 证明函数 在(0,+ )上是减函数.证明:设 是 上的任意两个实数,
且 则: 所以函数 在(0,+ )上是减函数.演练反馈
课堂小结:
本节课我们学习了函数单调性的知识,同学们要切记:单调性是对某个区间而言的,同时在理解定义的基础上,要掌握证明函数单调性的方法步骤,正确进行判断和证明。课后作业:
P46 习题2.3 4、6
函数的单调性观察下列函数中x,y的关系思考讨论在 上,
y随x的增大而减小在 上,
y随x的增大而减小 函数f (x)在给定区间上为增函数。如何用x与 f(x)来表述上升的图象?如何用x与 f(x)来表述下降的图象? 函数f (x)在给定区间上为减函数。y=f(x)yx0x1x2f(x1)f(x2)
设函数y=f(x)的定义域为I, 如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2,当x1
念。这个区间是定义域的子集。(3)单调区间:针对自变量 x 而言的。
若函数在此区间上是增函数,则为单调递增区间;
若函数在此区间上是减函数,则为单调递减区间.例1 如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,函数y=f(x)是增函数还是减函数. 解:函数f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中f(x)在区间[-5,-2),[1,3)上是减函数,
在区间[-2,1),[3,5]上是增函数.例题赏析(1)根据函数图像,指出函数在哪些区间上是减函数.(2)根据函数图像,指出函数在哪些区间上是增函数. 注意!用逗号间隔开演练反馈例2 证明函数 在R上是增函数.证明:设 是R上的任意两个实数,且 则:在R上是增函数. 例题赏析【判断函数单调性的步骤】1、设任意x1,x2属于给定区间,且x1
且 则: 所以函数 在(0,+ )上是减函数.演练反馈
课堂小结:
本节课我们学习了函数单调性的知识,同学们要切记:单调性是对某个区间而言的,同时在理解定义的基础上,要掌握证明函数单调性的方法步骤,正确进行判断和证明。课后作业:
P46 习题2.3 4、6
