用字母表示数

课题：3.1字母表示数
教学目标：
一、知识目标
1．知道在现实情境中字母表示数的意义。
2．会用字母表示一些简单问题中的数量关系和变化规律。
3．在探索规律的过程中感受从具体到抽象的归纳思想方法。
二、能力目标
1．经历字母表示数的过程，会用字母表示规律。
2．引导学生探索、归纳，提高学生分析问题，解决问题的能力。
三、情感目标
1．通过师生交往、互动，激发学生探究数学问题的兴趣，养成自主学习的好习惯。
2．在活动中，学会与他人交流与合作。
教学重点：体会字母表示数的意义，会用字母表示数量关系
教学难点：探索用代数式来表示规律的过程
教学过程：
一、创设情景，揭示课题
1．观察图片，说出它们表示的意义（学生举例）。在生活中常用图标表示某种意义，给我们的生活带来了方便。
2．唱儿歌：一只青蛙一张嘴，两只眼睛四条腿，扑通一声跳下水……
提问：两只青蛙呢？……
八只青蛙呢？……
十六只青蛙呢？……
同学们唱到这里就有一点困难了，但是儿歌还能继续唱下去，想一想你能用一句话把这首儿歌唱完吗？思考一下，并与同桌交流。
二、温故知新
1．由于学生小学时已经初步涉及用字母表示数（如用字母表示运算律、面积、周长等），通过回顾由此增强学生对“字母表示数”的感性认识：字母不但可以表示数，而且可以简明地表达数学公式，用以揭示数学规律。
请同学们观察下面的式子：
加法交换律：a + b = b + a 乘法交换律：a×b = b×a
2．姐姐的年龄比弟弟大四岁，求姐姐的年龄。
弟弟的年龄 1 2 7 13
姐姐的年龄 5 6 11 17
你能用一个式子来表示姐弟年龄的关系吗？
3．带领同学们一起回忆长方形和圆的周长、面积公式。
问：同学们感受到字母表示数的优越性了吗？请谈谈你的感受。
设计一组练习，在老师的指导之下，逐步学会用字母表示数和数量关系。
小明今年岁，小明比小丽大2岁，小丽今年（ ）岁 。
小丽5走了，那么她的平均速度是（ ）
一件羊毛衫标价元，按标价的8折出售，则这件羊毛衫的售价是（ ）元。
某城市5年前人均收入为元，预计今年人均收入是5年前的2倍多500元，那么今年人均收入将达（ ）元。
某城市市区人口万人，市区绿地面积万平方米，则平均每个人拥有绿地（ ）平方米
如图，这个三角形的面积是（ ）
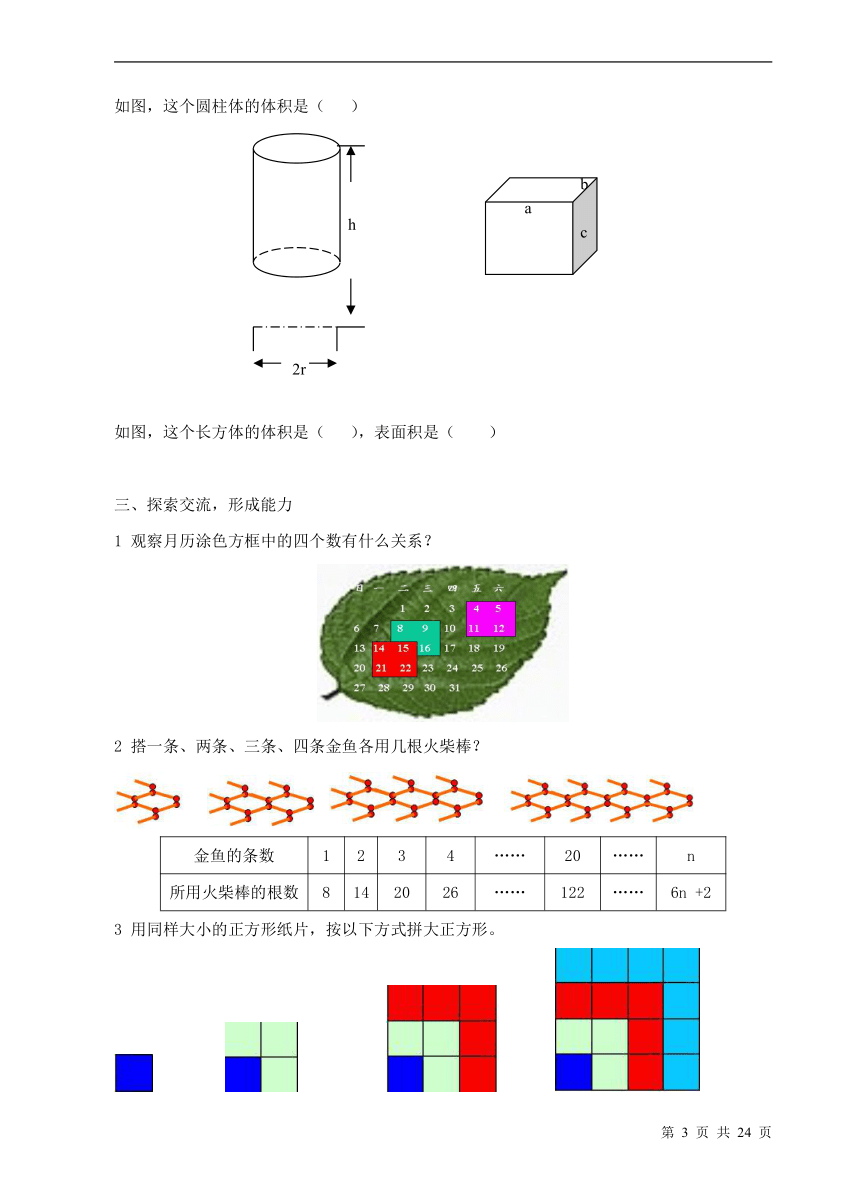
如图，这个圆柱体的体积是（ ）
如图，这个长方体的体积是（ ），表面积是（ ）
三、探索交流，形成能力
1 观察月历涂色方框中的四个数有什么关系？
2 搭一条、两条、三条、四条金鱼各用几根火柴棒？
金鱼的条数 1 2 3 4 …… 20 …… n
所用火柴棒的根数 8 14 20 26 …… 122 …… 6n +2
3 用同样大小的正方形纸片，按以下方式拼大正方形。
第一个图形有1个小正方形
第二个图形比第一个多（ ）小正方形
第三个图形比第二个多（ ）小正方形
第四个图形比第三个多（ ）小正方形
想一想：第5个图形比第4个多几个小正方形？
请在方格纸上画出第9个图形并验证你的猜想。
请问：第10个图形比第4个多几个小正方形？
第100个图形比第99个多几个小正方形？
第n 个图形比第n -1个多几个小正方形？
小组讨论，师生互动，全班交流。
“学生讨论”给予较充分的时间，使其经历探索规律的过程进一步感知用字母表示书、数给研究问题带来的方便，从而体会到用字母表示数的意义所在。
四、课堂练习：P80 练一练
五、归纳小结，整体把握
师生共同小结，用字母表示数的意义。用字母表示一些简单问题中的数量关系和变化规律。
六、布置作业
P81 习题3.1 1、2
七、教后反思：
课题：3.2代数式
教学目标：
一、知识目标：
1、在具体情景中进一步理解字母表示数的意义
2、能解释一些简单代数式的实际背景或几何意义，发展符号感
3、在具体情景中，能求出代数式的值，并解释它的实际意义
二、能力目标：
经历语言与代数式相互转化的过程，发展学生联想、类比能力，培养学生用数学语言进行表达和交流的能力
三、情感目标
在与他人交流的过程中，感受数学活动的生动魅力，激发学生学习数学的兴趣
教学重点：对代数式意义的理解，分析问题中的数量关系，列出代数式
教学难点：正确规范书写代数式和叙述代数式的意义
教学过程：
一、 创设情境
1. 小明去买苹果，苹果每千克1.5元，他买了a 千克，一共用去多少钱？
学生解答 1.5a
2. 请学生模仿列举日常生活中的例子，其他学生给以解答
从而得到以下式子：30a 、 9b 、 2ab+2bc +2ac 、abc
（为下面代数式的教学作铺垫）
二、探究新课
观察：30a、9b、2ab+2bc+2ac、abc…我们把这些式子都称为代数式
（1）引入代数式定义：像n、-2 、、0.8a、、2n +500、abc、2ab+2bc +2ac
等式子都是代数式。单独一个数或一个字母也是代数式。
（2）议一议
①薯片每袋a 元， 9折优惠，虾条每袋b 元8折优惠，两种食品各买一袋共需几元？
②一个长方形的宽是a m ，长是宽的2倍，这个长方形的长是多少？面积是多少？
③小明的爸爸携带了35kg的行李乘飞机，他的机票价是m 元，需付多少元行李费？
④环形花坛铺草坪，大圆半径为Rm，小圆半径为rm，需要草皮多少平方米？
3. 让学生先观察：30a 、 9b …你发现了什么？它们有什么公同的特征？
（引导学生说出它们都是字母与数相乘）
1）引入单项式定义：像0.9a，0.8b，2a，2a2，15×1.5%m等都是数与字母的积，这样的代数式叫单项式。单独一个数或一个字母也是单项式。
2）单项式中的数字因数叫做这个单项式的系数。
3）单项式中所有字母的指数的和叫做它的次数。
4. 观察2ab+2bc +2ac，n – 2…（引入多项式）
1）几个单项式的和叫做多项式。其中的每个单项式叫做多项式的一个项。
2）次数最高项的次数叫做这个多项式的次数。
5．小结
通过观察我们知道单项式和多项式都是代数式.
单项式和多项式统称整式
6. 举例
（1）某超市8月份营业额为m万元，9月份营业额比8月份增加了，该超市9月份营业额为多少万元？
（2）林老师用分期付款的方法购买汽车：首期付款a元，以后每月付款1500元，直至付清欠款，x个月后，林老师共付款多少元？
解：（1）该超市9月份营业额为万元；（2）林老师共付款（a+1500x）元。
注意：列代数式时，数字与字母、字母与字母相乘，乘号通常用·表示或省略不写，并且把数字写在字母的前面，除法运算通常写成分数的形式。
7. 做一做 列代数式：
1）苹果a元/kg，橘子b元/kg，买5kg苹果、8kg橘子应付多少元？
2）小明每步走am，小亮每步走bm，小明、小亮从小桥的两端相向而行，小明走5步、小亮走8步两人相遇，小桥长多少？
3）a 个三棱柱，b 个六棱柱共多少个面？
8. 议一议
1）从上面的“做一做“中你能发现什么？并与同学交流。
（引导学生说出同一个代数式可以表示不同意义的数量关系）
2）你能举例说明代数式2(x+y)表示的实际意义吗？
三、课堂练习：P85 练一练
四、总结
问题一 写出一些代数式，并指出哪些是单项式？哪些是多项式？说明单项式与多项式的联系与区别。
问题二 你能说出其中一个代数式的实际意义吗？
五、作业
P86 习题3.2 1
六、教后反思
课题：3.3 代数式的值（第1课时）
教学目标：
一、知识目标：
1、会求代数式的值，感受代数式求值可以理解为一个转换过程或某种算法
2、会利用代数式求值推断代数式所反映的规律
3、能理解代数式值的实际意义
二、能力目标：
通过代数式求值的教学活动，渗透数学中的函数思想，培养学生解决实际问题能力。
三、情感目标：
让学生体会从生活中发现数学和应用数学解决生活中问题的过程，品尝成功的喜悦，激发学生应用数学的兴趣
教学重点：求代数式的值
教学难点：利用代数式求值推断代数式所反映的规律。
教学过程：
一、创设情境：
1.求下图三角形的面积：
生：三角形的面积=
2．继续求下图三角形的面积
生：三角形的面积==9
3．用字母a表示三角形的底，h表示三角形的高，求当a=6，h=3时，三角形的面积。
三角形的面积== 9
4．揭示新课
（这节课我们就来学习3.3 代数式的值）
二、探索新知
1．师生共同学习例1
当a=-2、b=-3时，求代数式2a2-3ab+b2的值。
教师写出例1的全部过程（主要规范学生做此类题目的格式）
解：当a=-2、b=-3时,
2a2-3ab+b2
=2×(-2)2-3×(-2)×(-3)+(-3)2
=2×4-3×(-2)×(-3)+9
=8-18+9
=-1
2．补充例题
当x=2、y=-3时，求代数式-3x3-5y2的值。（由学生仿照例1完成）
解：当x=2、y=-3时，
-3x3-5y2
=-3×23-5×(-3)2
=-3×8-5×9
=-24-45
=-69
3．议一议
x -4 -3 -2 -1 0 1 2 3 4
2x+5
2(x+5)
先让学生完成表格
从这张表格上你获得了哪些信息？
(1)随着值的逐渐增大，两个代数式的值怎样变化？
(2)当代数式2x +5的值为25时，代数式2（x +5）的值是多少
4．巩固练习
（1）完成练一练 1.填表
x -1 0 0 9
x2
3x+1
x2+2x+1
（2）剪绳子：
1）将一根绳子对折1次再从中剪一刀，绳子变成（ ）段；将一根绳子对折2次再从中剪一刀，绳子变成（ ）段；将一根绳子对折3次再从中剪一刀，绳子变成（ ）段；
2）将一根绳子对折n 次再从中剪一刀，绳子变成（ ）段；
3) 根据（2）的结论，将一根绳子对折10 次再从中剪一刀，绳子变成（ ）段；
（探索本题中的规律较为困难，教学中让学生具体地“做” 用绳子、剪刀操作，然后再分析、思考。）
（3）用火柴棒按下图的方式搭正方形
1）搭n 个这样的正方形需要（ ）根火柴棒；
2) 搭100 个这样的正方形需要（ ）根火柴棒；
三、小结
通过本节课的学习，你学到了什么？还有什么疑问？
四、 布置作业
P91 习题3.3 1
五、教后反思：
课题：3.3代数式的值（第2课时）
教学目标：
1．能读懂计算程序图（框图），会按照规定的程序计算代数式的值，会按照要求设计简单的计算程序，初步感受“算法”的思想。
2. 在计算代数式的值的过程中，感受数量的变化及其联系。
教学重点：
会按照规定的程序计算代数式的值，会按照要求设计简单的计算程序。
教学难点：
初步感受“算法”的思想。
教学过程：
一、创设情境
小明的爸爸存入3年期的教育储蓄8650元（3年期教育储蓄的年利率为2.52%，免缴利息税），到期后本息和（本金与利息的和）自动转存3年期的教育储蓄，像这样至少要储蓄几次才能使本息和超过10 000元。请你用如图所示的程序，用计算器帮小明的爸爸算一算。
分析：小明的爸爸存入3年期教育储蓄8650元，到期后的本息和为多少？如果不满10 000元，再将所得的本息和续存3年期教育储蓄；到期后的本息和能满10 000元吗？如果不满，再继续储蓄……直至超过10 000元。
师：如何简明地表示这样的计算过程呢？
（引导学生讨论交流，继而组织学生阅读课本的计算框图，并向学生说明设计计算框图的规范要求）
二、探究感悟
师生共同操作“做一做”
1）按计算程序计算并填写下表：（程序—代数式—求值）
输入 -2.5 -0.49 0 1.99
输出
2）请你先设计出计算代数式3x2-5的值的计算程序（设计计算程序即：回忆有理数混合运算顺序）再计算并填写下表：（代数式—程序—求值）
x -1 0 1
3x2-5
三、巩固练习
(1) 练一练1.填表：
x -2 -1 0 1 2
2(x-3)
-5(x+1)
(2) 在下列计算程序中填写适当的数或转换步骤：
四、小结
（本节内容实际在复习有理数混合运算的运算顺序）
1．如果先给你计算程序，第一步把计算程序要表达的代数式表示出来。第二步实质在做求代数式值的工作。
2．如果给你代数式让你设计计算程序，只要严格按照有理数混合运算的运算顺序再结合设计计算框图的规范要求来设计。
3．通过本节课的学习你收获了哪些？还有什么疑问？
五、布置作业
P92 习题3.3 2、3、4
六、课后反思
课题：3.4 合并同类项（第1课时）
教学目标：
1、了解同类项的概念,能识别同类项.
2、会合并同类项.
3、知道合并同类项所依据的运算律.
教学重点：会合并同类项.
教学难点：知道合并同类项所依据的运算律.
教学过程：
一、创设情境
1、星期天，小明上街买了4个苹果，8个橘子，7个香蕉。妈妈不知道小明已经买了水果，于是，下班后妈妈从街上又买来5个苹果 ，10个橘子，6个香蕉，问：苹果，橘子，香蕉一共各有多少个？
生：4个苹果 + 5个苹果 = 9个苹果
8个橘子 + 10个橘子 = 18个橘子
7个香蕉 + 6个香蕉 = 13个香蕉
师：你们是根据什么来求和的？（引导学生说出苹果是一类，橘子是一类，香蕉是一类）
2、下图为某学校校园的总体规划图（单位：m），试计算这个学校的占地面积。
小丽说：学校的占地面积可以用代数式表示为100a+200a+240b+60b
小明说：也可以表示为(100+200)a+(240+60)b
可以看出：100a+200a+240b+60b=(100+200)a+(240+60)b
由此可知：计算100a+200a，可以先把它们的系数相加，再乘a；
计算240b+60b，可以先把它们的系数相加，再乘b。
引入新课：这节课我们就来学习3.4合并同类项
二、探索新课:
1. 议一议：
100a 和200a 、240b 和60b 、5ab2和-13ab2、-9x2y3和5x2y3有什么共同特点？
1）所含字母相同
2）相同字母的指数相同
2. 揭示定义：
所含字母相同，并且相同字母的指数相同，向这样的项是同类项。
3. 做一做：把下列各式的同类项合并成一项，并说出你计算的理由：
(1) 7a -3a=
(2) 4x2+2x2=
(3) 5ab2-13ab2=
(4) -9x2y3+5x2y3=
(学生先“做“，在“做”中不断感受，再明晰法则。其意图是引导学生经历“从感性到理性”的认识过程，更好地理解、掌握合并同类项法则。)
把同类项合并成一项叫做合并同类项
揭示合并同类项的法则：同类项的系数相加，所得的结果作为系数，字母和字母的指数不变。
4. 例1：合并同类项：
（1）-3x+2y-5x-7y；
解：-3x+2y-5x-7y
=(-3x-5x)+(2y-7y) 加法交换律
=(-3-5)x+(2-7)y 合并同类项法则、有理数加法法则
=-8x-5y
(括号内的说理,只在课堂上结合具体的计算进行口头训练,对学生的课外作业不必这样要求.)
（2）a2-3ab+5-a2-3ab-7
解：a2-3ab+5-a2-3ab-7
=(a2-a2)+(-3ab-3ab)+(5-7)
=(1-1)a2+(-3-3)ab+(-2)
=-6ab-2
5．练一练：P96
三、小结
(1) 本节课你学到了哪些知识 (生: 同类项,合并同类项)
(2) 请你举例说明同类项.
(3) 举例说明怎样合并同类项.
四、布置作业
P97 习题3.4 2
五、教后反思
课题：3.4 合并同类项（第2课时）
教学目标：
1、了解同类项的概念,能识别同类项.
2、会合并同类项，并将数值代入求值.
3、知道合并同类项所依据的运算律.
教学重点：会合并同类项，并将数值代入求值.
教学难点：知道合并同类项所依据的运算律.
教学过程：
一、创设情境
1、所含字母相同，并且相同字母的指数相同，向这样的项是同类项。
2、把同类项合并成一项叫做合并同类项。
3、合并同类项的法则：同类项的系数相加，所得的结果作为系数，字母和字母的指数不变。
二、探索新课:
1、例2 合并同类项5m3-3m2n-m3+2nm2-7+2m3中的同类项。
解：5m3-3m2n-m3+2nm2-7+2m3
=(5m3-m3+2m3)+( -3m2n+2m2n)-7
=(5-1+2)m3+(-3+2)m2n-7
=6m3-m2n-7
2、做一做：
求代数式2x3-5x2+x3+9x2-3x3-2的值，其中x=1。与同学交流你的做法。
解：2x3-5x2+x3+9x2-3x3-2
=2x3+x3-3x3-5x2+9x2-2
=(2+1-3)x3+(-5+9)x2-2
=4x2-2
当x=1时
原式=4×12-2=4-2=2
3、总结：
求代数式的值时，如果代数式中含有同类项，通常先合并同类项再代入数值进行计算。
4、练一练：
P97 练一练1、2
P98 4
1、合并同类项：
(1) a2-3a+5+a2+2a-1
(2) -2x3+5x2-0.5x3-4x2-x3
(3) 5a2-2ab+3b2+ab-3b2-5a2
(4) 5x3-4x2y+2xy2-3x2y-7xy2-5x3
2、求下列各式的值：
(1) 6y2-9y+5-y2+4y-5y2，其中
(2) 3a2+2ab-5a2+b2-2ab+3b2，其中a=-1，
三、小结
本节课你学到了哪些知识
四、布置作业
P98 习题3.4 3、5
五、教后反思
课题：3.5 去括号(第1课时)
教学目标：
1、会用去括号进行简单的运算。
2、经历得出去括号法则的过程，了解去括号法则的依据。
教学重点：
经历得出去括号法则的过程，了解去括号法则的依据。
教学难点：
经历得出去括号法则的过程，了解去括号法则的依据。
教学过程：
一、创设情境：
问：防护林带有多长？水渠有多长？
防护林带长为(3a+3a+4b+4b)+(a+b)
水渠长为(3a+3a+3a+4b+4b)-(a+b)
问：怎样去掉这2个式子中的括号呢？
二、填表导入：
a b c a+(-b+c) a-b+c a-(-b+c) a+b-c
-5 2 -1
-6 -4 3
-9.5 -5 -7
从这张表中你发现了什么？请与同学交流。（组织学生讨论交流，鼓励学生用自己的语言叙述去括号法则）
（教学中可以赋予a,b,c更多的值进行计算，以使学生确信a+(-b+c)与a-b+c的值相等，a-(-b+c)与a+b-c的值相等。）
思考：去括号前后，括号里各项的符号有什么变化？
三、揭示新课
1.师生共同揭示去括号法则：
括号前面是“+”号，把括号和它前面的“+”号去掉，括号里各项的符号都不改变。
括号前面是“-”号，把括号和它前面的“-”号去掉，括号里各项的符号都要改变。
2.试一试
(1)计算：
1) （3a +3a +4b +4b）+ (a+b)
2) （3a +3a +4b +4b）—(a+b)
（本题实际解决课前留下的疑问“怎样去掉这两个式子中的括号呢？”）
(2)根据运算律去括号：
1) a+(-b-c)
2) a-(-b-c)
（强调“去括号”实际上就是应用乘法分配律）
3.例1先去括号，再合并同类项：
(1) 5a-(2a-4b)
解：5a-(2a-4b)
=5a-2a+4b
=3a+4b
(2) 2x2+3(2x-x2)
解：2x2+3(2x-x2)
=2x2+6x-3x2 括号内每项都要乘3
=-x2+6x
（教师示范解答过程，指导格式）
4.小结
在进行去括号时，要利用去括号的法则，弄清括号前面是“+”号还是“—”号。
四、课堂小结：
（1）去括号法则的依据实际上就是乘法对加法的分配律
（2）去括号时应注意括号前面是“+”号还是“—”号。
（3）在去掉括号后，如有同类项，则要把同类项合并。
通过本节课的学习你还有那些疑问？
五、布置作业：
P102 习题3.5 1
六、教后反思：
课题：4.5 去括号（第2课时）
教学目标：
1.会进行简单的整式加，减运算。
2.经历观察、归纳等教学活动过程，发展学生的合作精神和有条理的思考和探究的能力。
教学重点：
进行简单的整式加，减运算。
教学难点：
在活动中发展学生的合作精神及探索问题的能力
教学过程：
一、动手操作
1.准备三张如下图所示的卡片
用它们拼成各种形状不同的四边形，并计算它们的周长。
（鼓励学生把长方形和等腰三角形拼成各种图形，分别计算出它们的周长和面积）
这2个四边形周长的和是：
(4a+2b)+(2a+4b)=4a+2b+2a+4b=6a+6b
这2个四边形周长的差是：
(4a+2b)-(2a+4b)=4a+2b-2a-4b=2a-2b
2.教师揭示以上这些工作实际上是在进行整式的加减运算
3.回顾以上过程
思考：整式的加减运算要进行哪些工作？
生1：“去括号”
生2：“合并同类项”
师生小结：整式的加减实际上是“去括号”和“合并同类项”法则的综合应用，
二、揭示如何进行整式的加减运算
进行整式的加减运算时，如果有括号先去括号，再合并同类项。
1、例2 求2a2-4a+1与-3a2+2a-5的差.
（本题首先带领学生根据题意列出式子，强调要把两个代数式看成整体，列式时应加上括号）
解：(2a2-4a+1)-(-3a2+2a-5)
=2a2-4a+1+3a2-2a+5
=5a2-6a+6
拓展练习
求多项式2x-3y+7与6x-5y-2的和.
提问：你有哪些计算方法？
（可引导学生进行竖式计算，并在练习中注意竖式计算过程中需要注意什么？）
(1) (2x-3y+7)+(6x-5y-2)
(2) (-3x2-x+2)+(4x2+3x-5)
(3) (4a2-3a)+(2a2+a-1)
(4) (x2+5xy-y2)-(x2+3xy-2y2)
(5) 2(1-a+a2)-3(2-a-a2)
2、例3先化简下式，再求值：5(3a2b-ab2)-4(-ab2+3a2b)，其中a=-2，b=3
做此类题目应先与学生一起探讨一般步骤：
1、去括号；
2、合并同类项；
3、代入求值。
解：5(3a2b-ab2)-4(-ab2+3a2b)
=15a2b-5ab2+4ab2-12a2b
=3a2b-ab2
当a=-2，b=3时
原式=3×(-2)2×3-(-2)×32=36+18=54
三、课堂练习：P102 练一练
四、课堂小结
1.进行整式的加减运算时，如果有括号先去括号，再合并同类项。
2.进行化简求值计算时（1）去括号。（2）合并同类项。（3）代入求值
3.通过本节课的学习你还有哪些疑问？
五、布置作业：P103 习题3.5 2、3、4
六、课后反思
1×2=2×1
1×= × 1
1 +2 = 2 + 1;
(-4)+2.6=2.6+(-4);
h
a
a
b
c
h
2r
每位旅客免费携带20kg行李，超重部分每千克按飞机票价格的1.5%付行李费。
35kg
a
h
6
3
输入8500
×(1+3.24%×3)
>10000
输出
是
否
输入x
×3
-5
输出____
输入x
输出3x2-5
输入____
+1
( )2
输出25
输入2
输出-15
输入2
( )2
+1
输出______
教学区
操 场
学生活动中心
图
书
馆
a
b
60
240
200
100
蓄水池
农 田
3a
4b
b
a
防护林
水渠
a
a
a
b
b
b
b
b
b
a
a
a
a
a
a
a
b
b
b
b
b
b
b
b
周长=(b+a+b)+a+a+a
=b+a+b+a+a+a
=4a+2b
周长=(b+a)+(b+a)+b+b
=b+a+b+a+b+b
=2a+4b
第 1 页 共 24 页