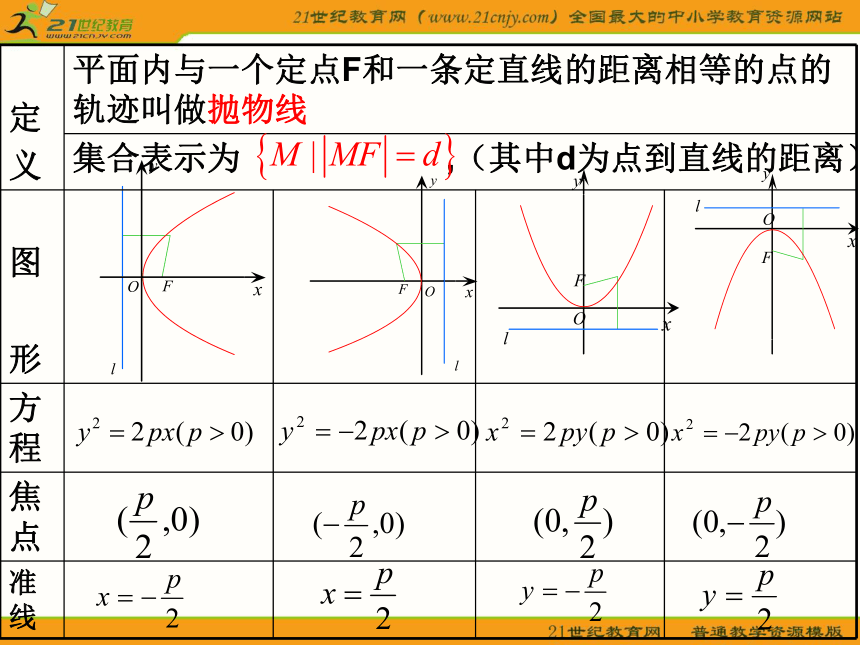
抛物线的简单几何性质
图片预览







文档简介
课件27张PPT。圆锥曲线抛物线的简单几何性质思维
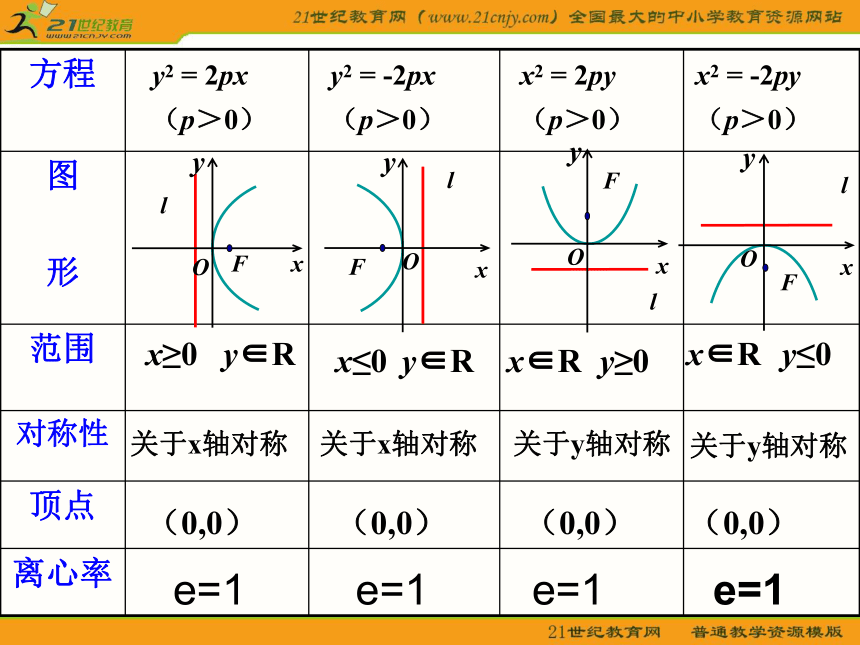
导图学习目标1.类比椭圆学习掌握抛物线的 简单几何性质2.自觉运用抛物线的几何性质 解答抛物线的有关问题3.在对抛物线几何性质的讨论中,注意数与形的结合与转化 练习: 填出下列抛物线的焦点坐标和准线方程 y轴的右侧X轴正向右上方和右下方抛物线的轴x1.范围:2.对称性:抛物线的顶点焦点的距离和它到准线的距离的比,3.顶点:4.离心率:此抛物线的顶点为坐标原点 y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0) e=1 e=1 e=1 e=1例1、已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M ,求它的标准方程.解:∵抛物线关于x轴对称,顶点在坐标原点,经过点M , ∴设它的标准方程为∵点M在抛物线上,∴
即p=2 ,∴所求抛物线方程是以y2=4x思考:顶点在坐标原点,对称轴是坐标轴,并且经过点M 的抛物线有几条?求出它们的标准方程.抛物线标准方程的求法:①直接法、②待定系数法——先定位、后定量先定位后定量练习:求满足下列条件的抛物线的方程 (1)顶点在原点,焦点是(0,-4)(2)顶点在原点,准线是x=4(3)焦点是F(0,5),准线是y=-5(4)顶点在原点,焦点在x轴上,
过点A(-2,4)例2.斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长.解:由抛物线 ,得 ∴焦
点F的坐标为(1,0),由(1)代入(2),得,∵斜率为1的直线 经过抛物线的焦点F,
∴直线 的方程为由∴由两点间的距离公式,得线段AB的长为8例2.斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点, 求线段AB的长.B’A’解:由抛物线 ,得 ∴焦
点F的坐标为(1,0),由(1)代入(2),得,∵斜率为1的直线 经过抛物线的焦点F,
∴直线 的方程为由设A,B两点到准线的距离分别是线段AB的长为8例2.斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点, 求线段AB的长.焦点弦的长的求法:到焦点的距离转为到准线的距离l通径这条弦通常称为结论:①求弦长一般要解方程组,
用韦达定理来求,若直线的斜率
为 ,则弦长公式为|AB|=③过抛物线焦点的直线截得的 弦称为焦点弦②抛物线上的点与焦点的连线
称为焦半径,它的长转为到
焦点的距离,|PF|=弦长|AB|=|AF|+|BF| =变式练习: 已知过抛物线 的焦点F弦长为36,求弦所在的直线方程, ,即∴弦所在的直线方程为小结:本节主要学习内容1、抛物线的简单几何性质的探究2、根据抛物线的几何性质求抛物线的标准方程3、对焦半径公式的应用和焦点弦的理解,在解题过程中必须明白数形结合的思想的重要性。范围
对称性
顶点
离心率抛物线标准方程的求法:
直接法、待定系数法
——先定位、后定量
抛物线上 的点(x0,y0)与焦点的连线通常称为焦半径,焦半径的长等于
焦点弦的长的求法:到焦点的距离转为到准线的距离检测练习:
1.根据下列条件,求抛物线的方程.
(1)顶点在原点,对称轴是x轴,
顶点到焦点的距离等于8.
(2)顶点在原点,焦点在y轴
上,且过P(4,2)点.
(3)顶点在原点,焦点在y轴上,
其上点P(m,-3)到焦点距离为5
,(1)(2)(3)2.过抛物线直线交抛物线于两点,如果那么(A)10 (B)8 (C)6 (D)4的焦点作为( )B3.过抛物线焦点F的直线与抛物线
交于A、B两点,若A、B在准线上的
射影是A1,B1,则∠A1FB1等于
4.抛物线顶点在原点,以坐标轴
为对称轴,过焦点且与y轴垂直的
弦长为16,求抛物线方程.
90°5.若抛物线 上一点M到准线及对称轴的距离分别是10和6,求点M的横坐标和的 值9,2或1,18 谢
谢
导图学习目标1.类比椭圆学习掌握抛物线的 简单几何性质2.自觉运用抛物线的几何性质 解答抛物线的有关问题3.在对抛物线几何性质的讨论中,注意数与形的结合与转化 练习: 填出下列抛物线的焦点坐标和准线方程 y轴的右侧X轴正向右上方和右下方抛物线的轴x1.范围:2.对称性:抛物线的顶点焦点的距离和它到准线的距离的比,3.顶点:4.离心率:此抛物线的顶点为坐标原点 y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0) e=1 e=1 e=1 e=1例1、已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M ,求它的标准方程.解:∵抛物线关于x轴对称,顶点在坐标原点,经过点M , ∴设它的标准方程为∵点M在抛物线上,∴
即p=2 ,∴所求抛物线方程是以y2=4x思考:顶点在坐标原点,对称轴是坐标轴,并且经过点M 的抛物线有几条?求出它们的标准方程.抛物线标准方程的求法:①直接法、②待定系数法——先定位、后定量先定位后定量练习:求满足下列条件的抛物线的方程 (1)顶点在原点,焦点是(0,-4)(2)顶点在原点,准线是x=4(3)焦点是F(0,5),准线是y=-5(4)顶点在原点,焦点在x轴上,
过点A(-2,4)例2.斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长.解:由抛物线 ,得 ∴焦
点F的坐标为(1,0),由(1)代入(2),得,∵斜率为1的直线 经过抛物线的焦点F,
∴直线 的方程为由∴由两点间的距离公式,得线段AB的长为8例2.斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点, 求线段AB的长.B’A’解:由抛物线 ,得 ∴焦
点F的坐标为(1,0),由(1)代入(2),得,∵斜率为1的直线 经过抛物线的焦点F,
∴直线 的方程为由设A,B两点到准线的距离分别是线段AB的长为8例2.斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点, 求线段AB的长.焦点弦的长的求法:到焦点的距离转为到准线的距离l通径这条弦通常称为结论:①求弦长一般要解方程组,
用韦达定理来求,若直线的斜率
为 ,则弦长公式为|AB|=③过抛物线焦点的直线截得的 弦称为焦点弦②抛物线上的点与焦点的连线
称为焦半径,它的长转为到
焦点的距离,|PF|=弦长|AB|=|AF|+|BF| =变式练习: 已知过抛物线 的焦点F弦长为36,求弦所在的直线方程, ,即∴弦所在的直线方程为小结:本节主要学习内容1、抛物线的简单几何性质的探究2、根据抛物线的几何性质求抛物线的标准方程3、对焦半径公式的应用和焦点弦的理解,在解题过程中必须明白数形结合的思想的重要性。范围
对称性
顶点
离心率抛物线标准方程的求法:
直接法、待定系数法
——先定位、后定量
抛物线上 的点(x0,y0)与焦点的连线通常称为焦半径,焦半径的长等于
焦点弦的长的求法:到焦点的距离转为到准线的距离检测练习:
1.根据下列条件,求抛物线的方程.
(1)顶点在原点,对称轴是x轴,
顶点到焦点的距离等于8.
(2)顶点在原点,焦点在y轴
上,且过P(4,2)点.
(3)顶点在原点,焦点在y轴上,
其上点P(m,-3)到焦点距离为5
,(1)(2)(3)2.过抛物线直线交抛物线于两点,如果那么(A)10 (B)8 (C)6 (D)4的焦点作为( )B3.过抛物线焦点F的直线与抛物线
交于A、B两点,若A、B在准线上的
射影是A1,B1,则∠A1FB1等于
4.抛物线顶点在原点,以坐标轴
为对称轴,过焦点且与y轴垂直的
弦长为16,求抛物线方程.
90°5.若抛物线 上一点M到准线及对称轴的距离分别是10和6,求点M的横坐标和的 值9,2或1,18 谢
谢
