函数y=asin(ωx+φ)的图象
文档属性
| 名称 | 函数y=asin(ωx+φ)的图象 |

|
|
| 格式 | rar | ||
| 文件大小 | 296.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-23 00:00:00 | ||
图片预览








文档简介
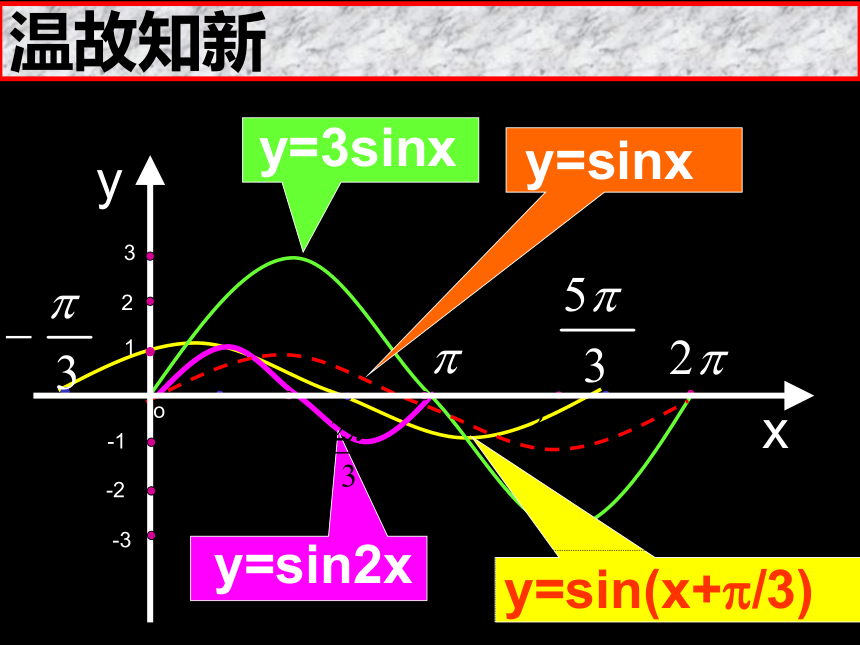
课件32张PPT。高一数学人民教育出版社中学数学室 编著一、简要复习y=Asinx、y=sinωx、y=sin(x+φ)的图象 (1)y=sin(x+?/3)
(2)y=sin2x
(3)y=3sinx 请同学们作出下面函数简图温故知新 y=sin2xy=3sinxy=sinxy=sin(x+?/3)xyo321-3-2-1参数φ, ω, A 在图象变换中的作用ΦωA (1)画出函数 y=Asin(ωx+φ) 的图象 (2)讨论函数
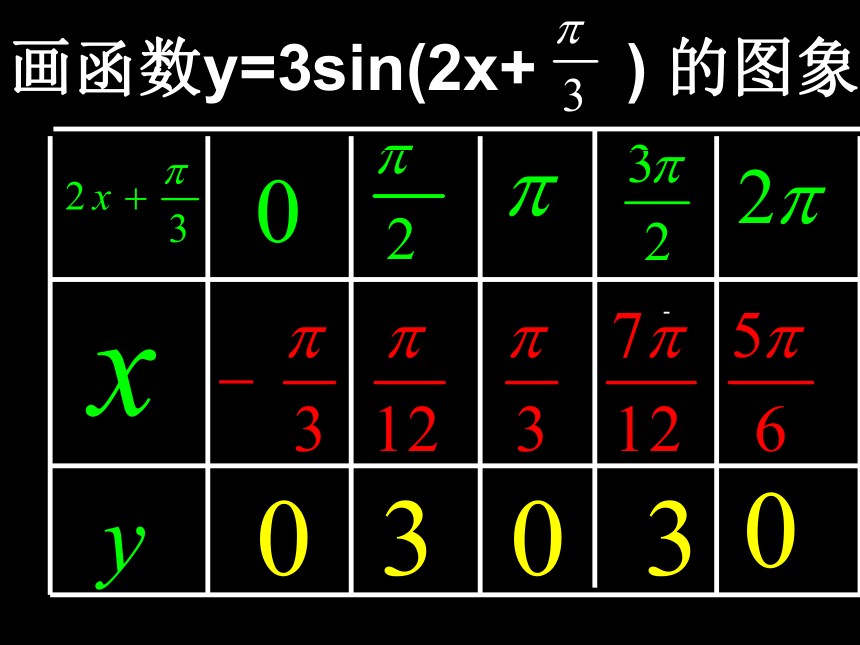
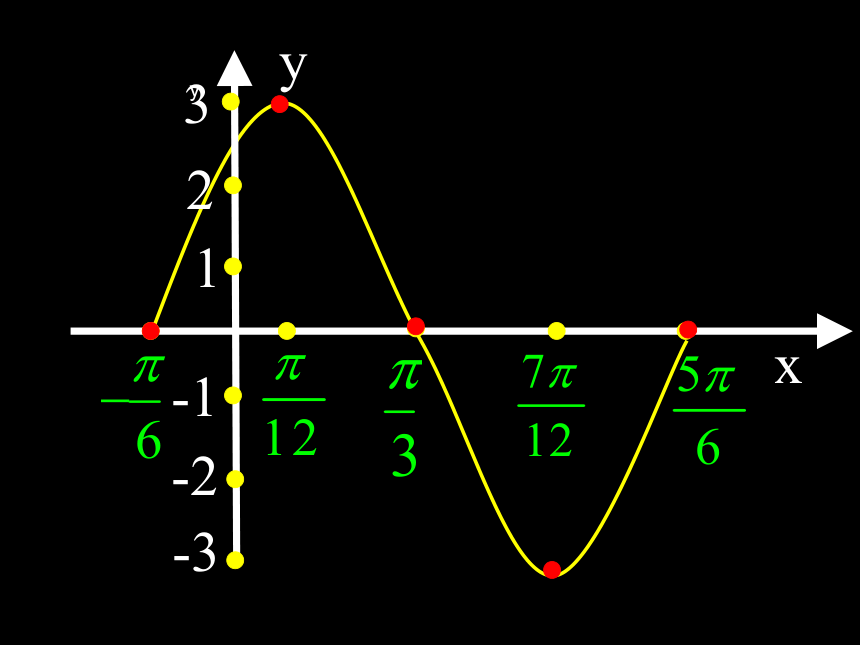
y=Asin(ωx+φ)图象的变换 二、本节例题讲解作函数 y = 3sin(2 + )的简图画函数y=3sin(2x+ ) 的图象- 函数 y = 3sin(2 + )
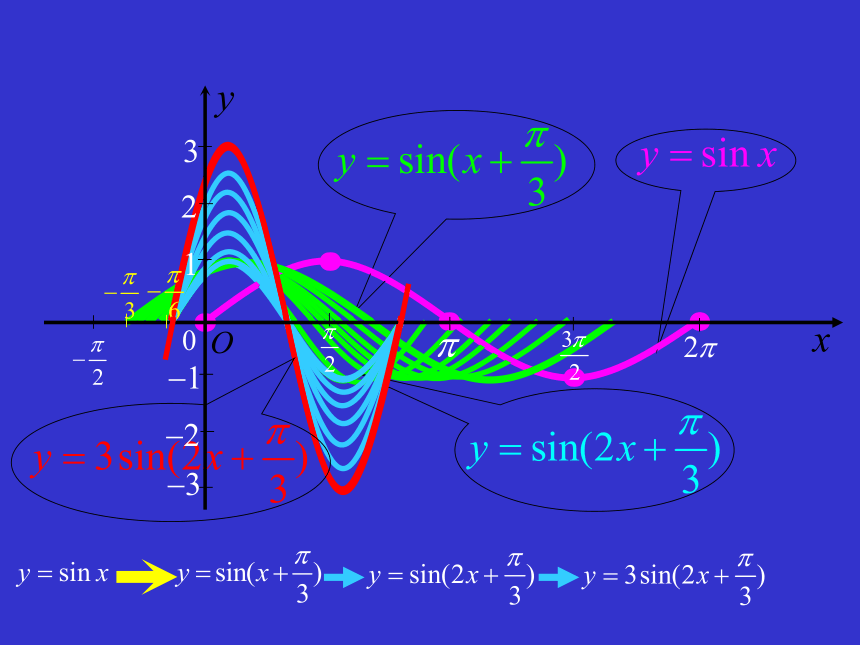
的图象,怎样由正弦曲线变换得到? 由以上图形的变化过程总结出此图像变化的基本步骤:函数 y=Sinxy=Sin(x+ ) 的图象y=Sin(2x+ ) 的图象y=3Sin(2x+ ) 的图象 总结由函数y=Asin(ωx+φ)y=sinx得出
的一般规律:y=Sin(? x+ ? ) 的图象函数 y=Sinxy=ASin(?x+ ? )的图象y=Sin(x+ ? ) 的图象(1)、为何不能由函数Y=sin2x的图像向左平移π/3个单位得到函数的Y=sin(2x+π/3)图像?(2)、由函数Y=sin2x的图像怎样移动可以得到Y =sin(2x+ π /3)图像?函数 y=Sinxy=Sin2x的图象y=Sin(2x+ ) 的图象y=3Sin(2x+ ) 的图象 总结由函数y=Asin(ωx+φ)y=sinx得出
的一般规律:y=Sin(? x+ ? ) 的图象函数 y=Sinxy=ASin(?x+ ? )的图象y=Sin(? x) 的图象当函数y=Asin(ωx+φ),(A>0,ω>0),x ∈[0,+∞)表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做这个振动的振幅;往复振动一次所需要的时间T=2π/ω,它叫做振动的周期;单位时间内往复振动的次数f=1/T=ω/2π,它叫做振动的频率;ωx+φ叫做相位,φ叫做初相(即当x=0时的相位).(1)为了得到函数y=3sin(x-π/5),x∈R的图象,只需把C上所有的点( )
(A)向左平行移动π/5个单位长度
(B)向右平行移动π/5个单位长度
(C)向左平行移动2π/5个单位长度
(D)向右平行移动2π/5个单位长度D 已知函数y=3sin(x+π/5),x∈R的图象为C. (2)为了得到函数y=3sin(2x+π/5),x∈R的图象,只需把C上所有的点( )
(A)横坐标伸长到原来的2倍,纵坐标不变
(B)横坐标缩短到原来的1/2倍,纵坐标不变
(C)纵坐标伸长到原来的2倍,横坐标不变
(D)纵坐标伸长到原来的1/2倍,横坐标不变B 已知函数y=3sin(x+π/5),x∈R的图象为C.(3)为了得到函数y=4sin(x+π/5),x∈R的图象,只需把C上所有的点( )
(A)横坐标伸长到原来的4/3倍,纵坐标不变
(B)横坐标缩短到原来的3/4倍,纵坐标不变
(C)纵坐标伸长到原来的4/3倍,横坐标不变
(D)纵坐标伸长到原来的3/4倍,横坐标不变C练习3:
用五点法作出函数的图象
并说明这个图象可由余弦函数的图象经过如何变换得到?2、函数 y = sinx 的图象与函数 y=Asin(?x+?)的图象间的变换关系。4、函数 y=Acos(?x+?) 的相关问题同样处理。3、函数y=Asin(?x+?)中A、?、?的物理意义书面作业题:
课本76页 2. (3)、(4) 3课后作业题:
本节内容所对配套练习题再见谢谢大家y=Sin(? x+ ? ) 的图象函数 y=Sinxy=ASin(?x+ ? )的图象y=Sin(x+ ? ) 的图象y=Sin(? x+ ? ) 的图象函数 y=Sinxy=ASin(?x+ ? )的图象y=Sin(? x) 的图象
(2)y=sin2x
(3)y=3sinx 请同学们作出下面函数简图温故知新 y=sin2xy=3sinxy=sinxy=sin(x+?/3)xyo321-3-2-1参数φ, ω, A 在图象变换中的作用ΦωA (1)画出函数 y=Asin(ωx+φ) 的图象 (2)讨论函数
y=Asin(ωx+φ)图象的变换 二、本节例题讲解作函数 y = 3sin(2 + )的简图画函数y=3sin(2x+ ) 的图象- 函数 y = 3sin(2 + )
的图象,怎样由正弦曲线变换得到? 由以上图形的变化过程总结出此图像变化的基本步骤:函数 y=Sinxy=Sin(x+ ) 的图象y=Sin(2x+ ) 的图象y=3Sin(2x+ ) 的图象 总结由函数y=Asin(ωx+φ)y=sinx得出
的一般规律:y=Sin(? x+ ? ) 的图象函数 y=Sinxy=ASin(?x+ ? )的图象y=Sin(x+ ? ) 的图象(1)、为何不能由函数Y=sin2x的图像向左平移π/3个单位得到函数的Y=sin(2x+π/3)图像?(2)、由函数Y=sin2x的图像怎样移动可以得到Y =sin(2x+ π /3)图像?函数 y=Sinxy=Sin2x的图象y=Sin(2x+ ) 的图象y=3Sin(2x+ ) 的图象 总结由函数y=Asin(ωx+φ)y=sinx得出
的一般规律:y=Sin(? x+ ? ) 的图象函数 y=Sinxy=ASin(?x+ ? )的图象y=Sin(? x) 的图象当函数y=Asin(ωx+φ),(A>0,ω>0),x ∈[0,+∞)表示一个振动量时,A就表示这个量振动时离开平衡位置的最大距离,通常把它叫做这个振动的振幅;往复振动一次所需要的时间T=2π/ω,它叫做振动的周期;单位时间内往复振动的次数f=1/T=ω/2π,它叫做振动的频率;ωx+φ叫做相位,φ叫做初相(即当x=0时的相位).(1)为了得到函数y=3sin(x-π/5),x∈R的图象,只需把C上所有的点( )
(A)向左平行移动π/5个单位长度
(B)向右平行移动π/5个单位长度
(C)向左平行移动2π/5个单位长度
(D)向右平行移动2π/5个单位长度D 已知函数y=3sin(x+π/5),x∈R的图象为C. (2)为了得到函数y=3sin(2x+π/5),x∈R的图象,只需把C上所有的点( )
(A)横坐标伸长到原来的2倍,纵坐标不变
(B)横坐标缩短到原来的1/2倍,纵坐标不变
(C)纵坐标伸长到原来的2倍,横坐标不变
(D)纵坐标伸长到原来的1/2倍,横坐标不变B 已知函数y=3sin(x+π/5),x∈R的图象为C.(3)为了得到函数y=4sin(x+π/5),x∈R的图象,只需把C上所有的点( )
(A)横坐标伸长到原来的4/3倍,纵坐标不变
(B)横坐标缩短到原来的3/4倍,纵坐标不变
(C)纵坐标伸长到原来的4/3倍,横坐标不变
(D)纵坐标伸长到原来的3/4倍,横坐标不变C练习3:
用五点法作出函数的图象
并说明这个图象可由余弦函数的图象经过如何变换得到?2、函数 y = sinx 的图象与函数 y=Asin(?x+?)的图象间的变换关系。4、函数 y=Acos(?x+?) 的相关问题同样处理。3、函数y=Asin(?x+?)中A、?、?的物理意义书面作业题:
课本76页 2. (3)、(4) 3课后作业题:
本节内容所对配套练习题再见谢谢大家y=Sin(? x+ ? ) 的图象函数 y=Sinxy=ASin(?x+ ? )的图象y=Sin(x+ ? ) 的图象y=Sin(? x+ ? ) 的图象函数 y=Sinxy=ASin(?x+ ? )的图象y=Sin(? x) 的图象
