函数的单调性

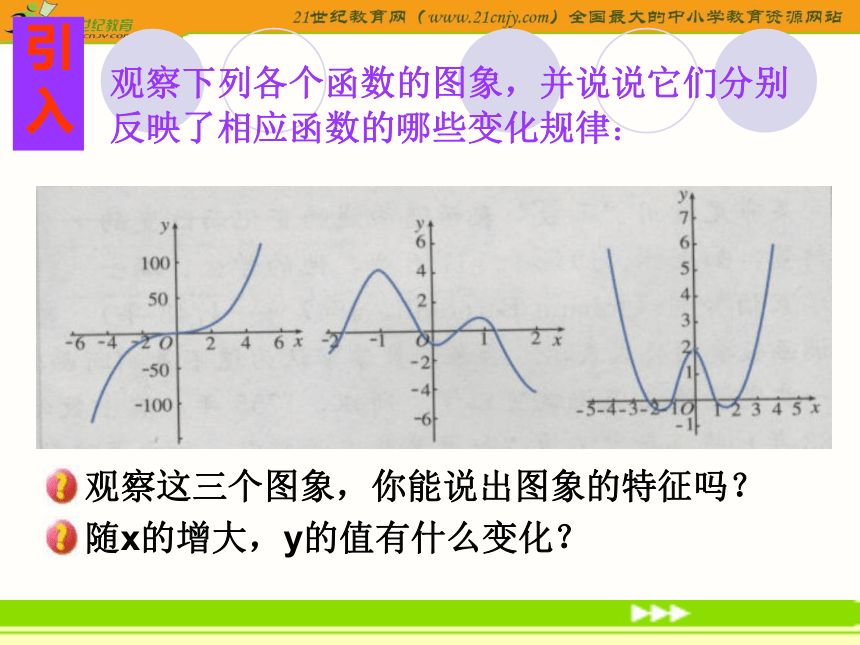
课件18张PPT。函数的单调性观察下列各个函数的图象，并说说它们分别反映了相应函数的哪些变化规律： 引 入画出下列函数的图象，观察其变化规律： f(x) = xf(x) = x21、从左至右图象上升还是下降 ____?
2、在区间 ________上，随着x的
增大，f(x)的值随着 ______ ．1、在区间 ____ 上，f(x)的值随着x的增大而 ______．
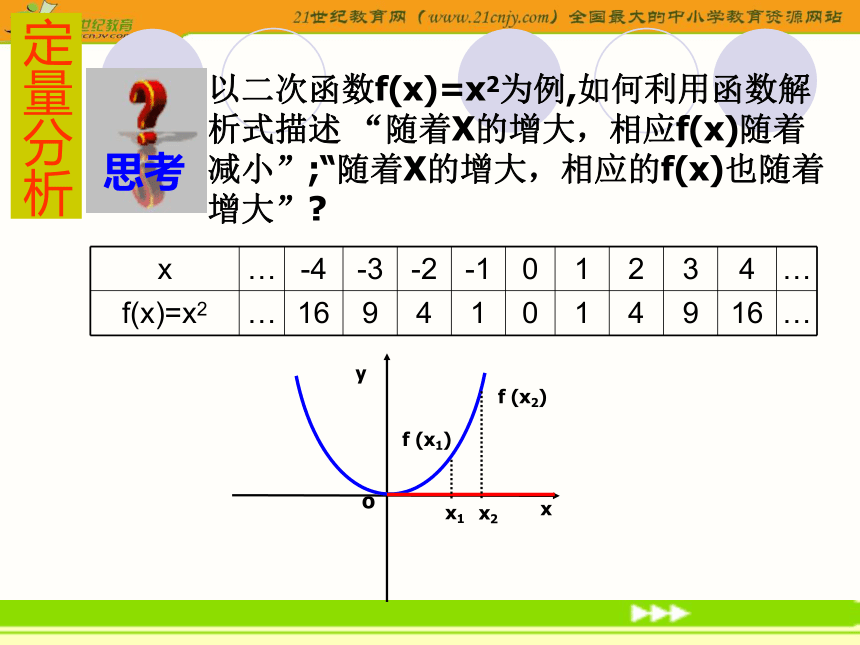
2、 在区间 _____ 上，f(x)的值随着x的增大而 _____． 上升(-∞,+∞)增大(-∞,0]减小(0,+∞)增大直观认识以二次函数f(x)=x2为例,如何利用函数解析式描述 “随着X的增大，相应f(x)随着减小”;“随着X的增大，相应的f(x)也随着增大”?定量分析说一说 在区间(0,+ ∞)上任取两个x1，x2得到f(x1)=x12 ,f(x2)=x22，当x1f(x2) 分别是增函数和减函数. 如果函数y=f(x)在某个区间上是增函数或是减函数，那么就说函数y=f(x)在这一区间具有（严格的）单调性，区间D叫做y=f(x)的单调区间. 函数的单调性定义说出下列三类函数的单调性在(-∞,+∞)是减函数
在(-∞,0)和(0,+∞)是减函数在(-∞,+∞)是增函数在(-∞,0)和(0,+∞)是增函数例1　　如图定义在闭区间 [-5，5] 上的函数y= f(x) 的图象，根据图象说出 y= f(x)的单调区间，以及在每一单调区间上 , y= f(x)是增函数还是减函数?　解：函数y= f(x)的单调区间有[-5，2），[-2，1），[1，3），[3，5]。其中 y= f(x)在区间[-5，2）， [1，3）上是减函数，在[-2，1）， [3，5]是增函数。练习注意：函数y= f(x)在[-5，2）∪[1，3）上不是减函数。可以说：函数y= f(x)在[-5，2）和[1，3）上是减函数若函数在两个区间上都是减函数，则在它们的并集上不一定是减函数.证明：根据单调性的定义，设V1，V2是定义域(0，+∞)上的任意两个实数，且V10, V2- V1 >0取值定号结论作差
变形例２ 练 习判断函数单调性的方法步骤 1、 任取x1，x2∈D，且x12、 作差f(x1)－f(x2)；
3、 变形（通常是因式分解和配方）；
4 、定号（即判断差f(x1)－f(x2)的正负）；
5、 下结论（即指出函数f(x)在给定的区间D上的单调性）． 利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤：　思考？ 画出反比例函数的图象．
1 、这个函数的定义域是什么？
2 、它在定义域I上的单调性怎样？证明　　　　　　　　　　　 你的结论． 定义域：(-∞,0)υ(0,+∞)思考： 解:证明：函数f(x)=1/x 在(0，+∞)上是减函数。证明：设x1,x2是(0，+∞)上任意两个实数，
且x1增（减）函数的图象有什么特点？如何根据图象指出单调区间？
怎样用定义证明函数的单调性？ 课堂小结1、书面作业：课本P4３习题1．3（A组）
　　第３、４题。　　　　 作 业谢谢　再见