高中数学课件2.1.2《离散型随机变量的分布列(二)》课件(新人教A版选修2-3)
文档属性
| 名称 | 高中数学课件2.1.2《离散型随机变量的分布列(二)》课件(新人教A版选修2-3) |  | |
| 格式 | rar | ||
| 文件大小 | 568.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-23 21:04:00 | ||
图片预览




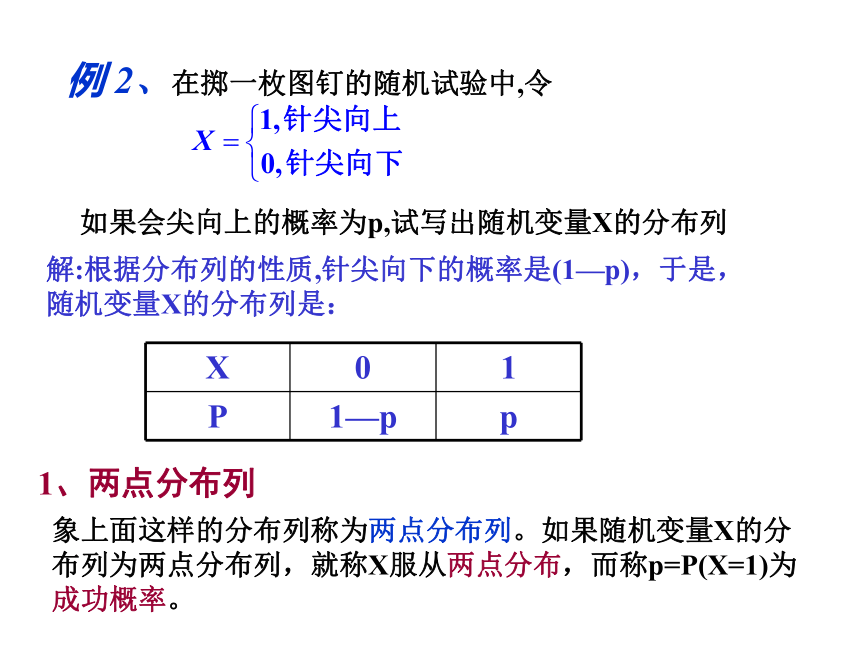


文档简介
课件14张PPT。离散型随机变量的分布列(2)回顾复习 如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量.1. 随机变量 对于随机变量可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.2.离散型随机变量3、离散型随机变量的分布列的性质:例1:已知随机变量 的分布列如下:-2-13210分别求出随机变量⑴;⑵的分布列.解:且相应取值的概率没有变化例1:已知随机变量 的分布列如下:-2-13210分别求出随机变量⑴;⑵的分布列.解:解:根据分布列的性质,针尖向下的概率是(1—p),于是,随机变量X的分布列是:1、两点分布列象上面这样的分布列称为两点分布列。如果随机变量X的分布列为两点分布列,就称X服从两点分布,而称p=P(X=1)为成功概率。练习:1、在射击的随机试验中,令X= 如
果射中的概率为0.8,求随机变量X的分布列。0,射中,
1,未射中2、设某项试验的成功率是失败率的2倍,用随机变量 去描述1次试验的成功次数,则失败率p等于( )
A.0 B. C. D.C例3:在含有5件次品的100件产品中,任取3件,试求:
(1)取到的次品数X的分布列;
(2)至少取到1件次品的概率.解:(1)从100件产品中任取3件结果数为从100件产品中任取3件,其中恰有K件次品的结果为 那么从100件产品中任取3件, 其中恰好有K件次品的概率为 一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件产品数,则事件{X=k}发生的概率为2、超几何分布称分布列为超几何分布例4:在某年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有10个红球和个20白球,这些球除颜色外完全相同。一次从中摸出5个球,至少摸到3个红球就中奖。求中奖的概率。例5:袋中有个5红球,4个黑球,从袋中随机取球,设取到一个红球得1分,取到一个黑球得0分,现从袋中随机摸4个球,求所得分数X的概率分布列。练:
盒中装有一打(12个)乒乓球,其中9个新的,3个旧的,从盒中任取3个来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量。求X的分布列。例6:在一次英语口语考试中,有备选的10道试题,已知某考生能答对其中的8道试题,规定每次考试都从备选题中任选3道题进行测试,至少答对2道题才算合格,求该考生答对试题数X的分布列,并求该考生及格的概率。例7:袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 。现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取到的机会是等可能的,用 表示取球终止时所需要的取球次数。
(1)求袋中原有白球的个数;
(2)求随机变量 的概率分布;
(3)求甲取到白球的概率。练习 从1~10这10个数字中随机取出5个数字,令
X:取出的5个数字中的最大值.试求X的分布列.具体写出,即可得 X 的分布列:解: X 的可能取值为5,6,7,8,9,10. 并且=——求分布列一定要说明 k 的取值范围!例 8、从一批有10个合格品与3个次品的产品中,一件一件的抽取产品,设各个产品被抽到的可能性相同,在下列两种情况下,分别求出取到合格品为止时所需抽取次数 的分布列。
(1)每次取出的产品都不放回该产品中;
(2)每次取出的产品都立即放回该批产品中,然后
再取另一产品。变式引申:1、某射手射击目标的概率为0.9,求从开始射击到击中目标所需的射击次数 的概率分布。
2、数字1,2,3,4任意排成一列,如果数字k 恰好在第k个位置上,则称有一个巧合,求巧合数 的分布列。一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球的个数是绿球个数的两倍,黄球个数是绿球个数的一半,现从该盒中随机取出一球,若取出红球得1分,取出绿 球得0分,取出黄球得-1分,试写出从该盒内随机取出一球所得分数ξ的分布列.
果射中的概率为0.8,求随机变量X的分布列。0,射中,
1,未射中2、设某项试验的成功率是失败率的2倍,用随机变量 去描述1次试验的成功次数,则失败率p等于( )
A.0 B. C. D.C例3:在含有5件次品的100件产品中,任取3件,试求:
(1)取到的次品数X的分布列;
(2)至少取到1件次品的概率.解:(1)从100件产品中任取3件结果数为从100件产品中任取3件,其中恰有K件次品的结果为 那么从100件产品中任取3件, 其中恰好有K件次品的概率为 一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件产品数,则事件{X=k}发生的概率为2、超几何分布称分布列为超几何分布例4:在某年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有10个红球和个20白球,这些球除颜色外完全相同。一次从中摸出5个球,至少摸到3个红球就中奖。求中奖的概率。例5:袋中有个5红球,4个黑球,从袋中随机取球,设取到一个红球得1分,取到一个黑球得0分,现从袋中随机摸4个球,求所得分数X的概率分布列。练:
盒中装有一打(12个)乒乓球,其中9个新的,3个旧的,从盒中任取3个来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量。求X的分布列。例6:在一次英语口语考试中,有备选的10道试题,已知某考生能答对其中的8道试题,规定每次考试都从备选题中任选3道题进行测试,至少答对2道题才算合格,求该考生答对试题数X的分布列,并求该考生及格的概率。例7:袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 。现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取到的机会是等可能的,用 表示取球终止时所需要的取球次数。
(1)求袋中原有白球的个数;
(2)求随机变量 的概率分布;
(3)求甲取到白球的概率。练习 从1~10这10个数字中随机取出5个数字,令
X:取出的5个数字中的最大值.试求X的分布列.具体写出,即可得 X 的分布列:解: X 的可能取值为5,6,7,8,9,10. 并且=——求分布列一定要说明 k 的取值范围!例 8、从一批有10个合格品与3个次品的产品中,一件一件的抽取产品,设各个产品被抽到的可能性相同,在下列两种情况下,分别求出取到合格品为止时所需抽取次数 的分布列。
(1)每次取出的产品都不放回该产品中;
(2)每次取出的产品都立即放回该批产品中,然后
再取另一产品。变式引申:1、某射手射击目标的概率为0.9,求从开始射击到击中目标所需的射击次数 的概率分布。
2、数字1,2,3,4任意排成一列,如果数字k 恰好在第k个位置上,则称有一个巧合,求巧合数 的分布列。一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球的个数是绿球个数的两倍,黄球个数是绿球个数的一半,现从该盒中随机取出一球,若取出红球得1分,取出绿 球得0分,取出黄球得-1分,试写出从该盒内随机取出一球所得分数ξ的分布列.
