13.2 不等式的基本性质

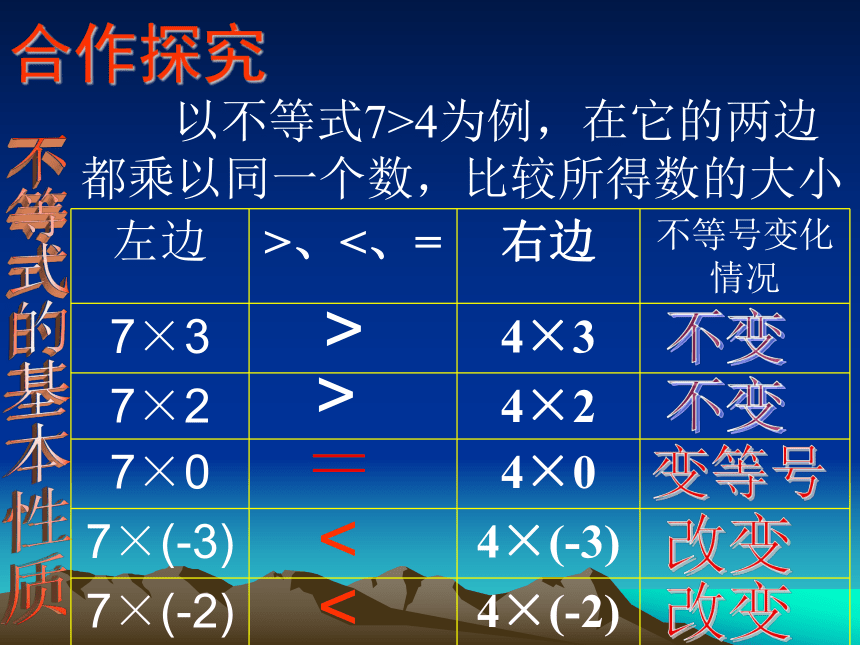
课件12张PPT。13.2不等式的基本性质规律探讨仿照下表，分组探讨不等式的性质1： 不等式的两边都加上（或减去）同一个数，不等号的方向不变．由上面的探讨我们可以得出：这个性质可以用数学语言表示为：＜＞合作探究不等式的基本性质 以不等式7>4为例，在它的两边
都乘以同一个数，比较所得数的大小>>＝<<不变不变变等号改变改变合作探究 不等式的性质2：如果a>b，
并且c>0，那么ac>bc． 不等式的性质3：如果a>b，
并且c<0，那么ac个正数，不等号方向不变；
　　不等式两边都乘以(或除以)同一
个负数，不等号方向改变．正数不变负数改变知识巩固：
1.用“＞”或“＜”在横线上填空，并在题后
括号内填写理由.
∵a＞b (2)∵ a＞b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m＞5n (4)∵4x＞5x
∴ -m ( ) ∴ x 0( )
(5)∵ ＜ (6)∵a-1＜8
∴ a 2b( ) ∴ a 9( ) ＞＞＞＜＜＜不等式基
本性质1不等式基
本性质3不等式基
本性质3不等式基
本性质1不等式基
本性质2不等式基
本性质1创新运用例1：已知a>b，判断下列不等式变形是
　　否正确，试说明理由．(2) ac2>bc2 ( )(3) a(c2+1)>b(c2+1) ( )达标反馈(1)．用“>”、“<”号填空② a>0，b>0，则ab 0③ 当a<0时，b 0时，ab<0<>>>达标反馈 (2)判断下列解不等式的过程是否正
确，若不正确，请改正．① -3x>7
-3x×(- 　 )>7×(- )x> -<<≤≤解 （1）根据不等式的性质1，两边都加上2得：
x－2＋2＜3＋2
即 x ＜5
（2）根据不等式的性质1，两边都减去5 x 得：
6 x －5 x ＜（5 x －1）－5 x
即 x ＜－1 根据不等式的基本性质，把下列不等式化成 x＜ 或 x＞ 的形式：
（1） x －2＜ 3 （2） 6 x ＜ 5 x －1
（3） x ＞5 （4） －4 x ＞3达标反馈课堂回顾在不等式两边同乘以(或除以)同一个正数，不等号方向不变，也就是说，如果a>b，并且c>0，那么，ac>bc；
在不等式两边同乘以(或除以)同一个负数，不等号方向改变，也就是说，如果a>b，并且c<0，那么ac比较运用不等式性质2或3时，与方程变形的联系与区别：在不等式的两边同乘以(或除以)一个不为0的数，注意乘数(或除数)的符号，正确确定不等号的方向．内容总结：作业 习题:1、2