5.2.1代数式

课件17张PPT。§5.2 代数式（1）第5章 代数式与函数的初步认识 （1）在用字母表示数时，字母与字母之间的 乘号，一般省略不写，或者乘号用“?” 表示。如第一题中的a乘以b一般写为ab或a?b。
（2）数字与字母相乘，数字一般放在字母的前面。如：2a
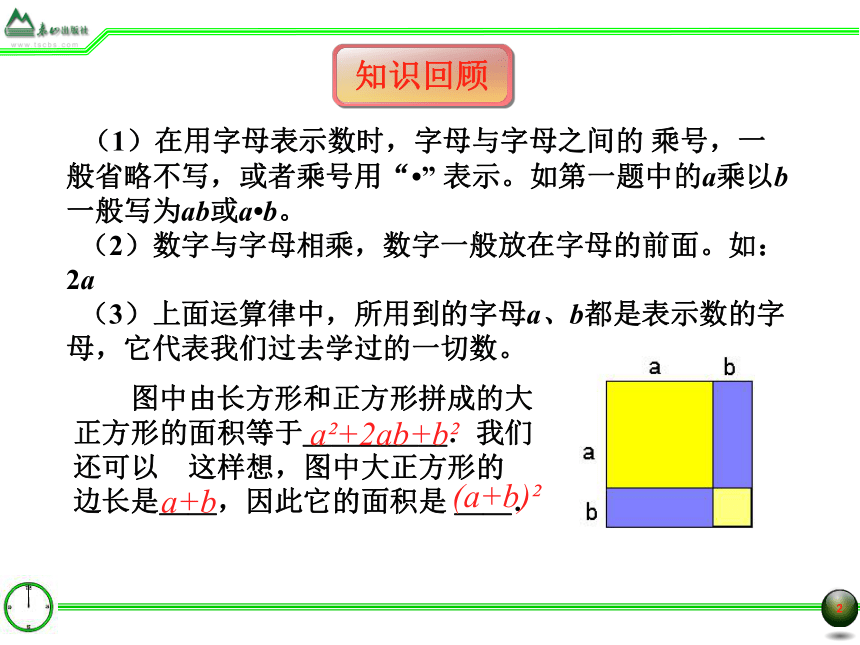
（3）上面运算律中，所用到的字母a、b都是表示数的字母，它代表我们过去学过的一切数。 图中由长方形和正方形拼成的大正方形的面积等于＿＿＿＿＿．我们还可以　这样想，图中大正方形的　边长是＿＿，因此它的面积是 ＿＿．
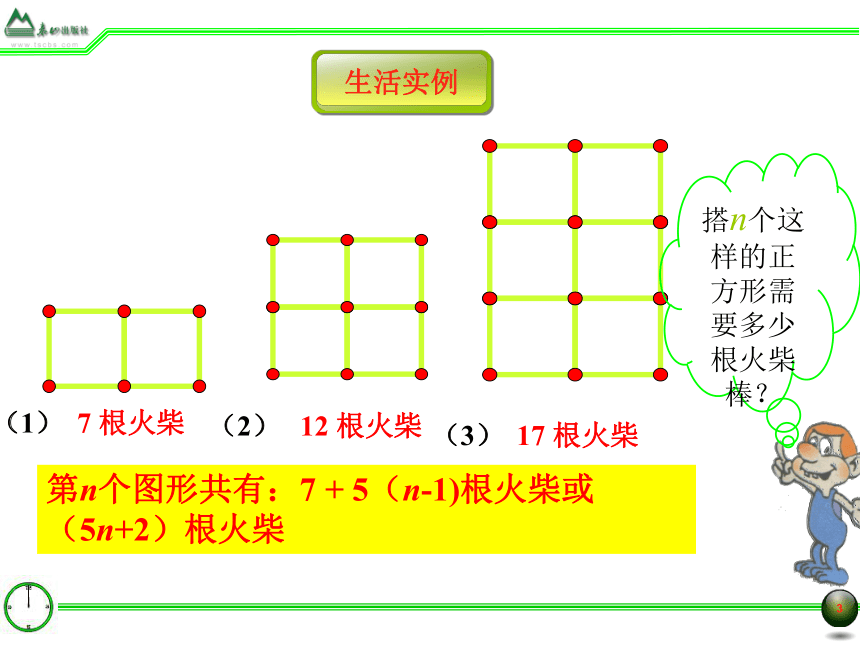
a2+2ab+b2a+b(a+b)2搭n个这样的正方形需要多少根火柴棒？第n个图形共有：7 + 5（n-1)根火柴或（5n+2）根火柴用字母表示数量关系:
1.大西洋是世界第二大洋。据测量，他的东西宽度每年
增加4厘米，经过n年将增加 厘米。
2.长方形的长和宽分别是a和b，正方形的边长是c，长
方形与正方形面积的和是 。
3.小亮用t秒走了s米，他的速度是为 米/秒.
4.小彬拿166元钱去买钢笔，买了单价为5元的钢笔n支
则剩下的钱为 元，他最多能买这种钢笔 支.
4n166－5n33ab+ 像5n+2 、4n、ab+ 、 、166－5n 、33的这样式子叫
代数式
注意：
1. 单独一个数或一个字母也是代数式。
2.式子不含“=”、“>”、“<”、“≤”、“≥” (1) a×b 通常写作 a·b 或 ab(3)如：a×3通常写作3a代数式的规范写法：｛(2) 1÷a 通常写作练习：判断下列式子哪些是代数式，哪些不是。答： （1）、（2）、（3）、（5）、（10）是代数式；
（4）、（6）、（7）、（8）、（9）不是。例1 .设字母a表示甲数，用代数式表示下列各题中的乙数：
（1）乙数比甲数大3的 （2）甲乙两数的和为10
（3）甲数是乙数的5倍 （4）乙数比甲数的平方少2解:（1）a+3 （2）10－a（4） （3） （1）3x+2y（2）3（x－5）像“x的3倍与y的2倍的和”、“x与5的差的3倍”等用文字表述数量关系的语言称为自然语言，而通过例1和例2我们把他们转化成了数学语言。可以看出在描述问题时数学语言比自然语言更简单明确。
解答一个含有数量关系的问题时，只要把问题中的自然语言译成数学语言就行了！

1.选择题：
（1）下列结论中正确的是（ ）
A.a是代数式，1不是代数式 B.1是代数式，a不是代数式
C.1与a都不是代数式 D.1与a都是代数式
（2）代数式2(m+n)的意义是（ ）
A.2m与n的和 B.m的2倍与n的和
C.m与n的和的2倍 D.m与n的2倍
2.用代数式表示：
（1）x的2倍与y的一半的差 （2）x的n倍与-1的和
DC3.将下列代数式用自然语言表示：
（1）5-4a （2）(a+b)(a-b)
4.电教室里的座位的排数是m,用代数式表示：
（1）若每排座位数是排数的 倍，则电教室里共有多少个座位？
（2）若第一排的座位数是a，并且后一排总比前一排的座位数多1个，则电教室里第m排有多少个座位？4题解:（1） m×m= m2（每排座位数： m）(2) a+m-1aa+1a +1 +1a +1 +1第1排第2排第3排第m排m-1{……+ …+1你做对了吗？例3用代数式表示：（1）某数的3倍与2的差的平方
（2）三个连续偶数的和解 （1）如果把某数用x表示，那么某数的3倍与2的差的平方可以表示为
（2）如果用2n（n为整数）表示中间的一个偶数，那么三个连续偶数可以表示为2n-2，2n,2n+2。
三个连续偶数的和是(2n-2)+2n+(2n+2)。某数用x表示，偶数用2n表示，奇数可以怎么表示呢？ 奇数可以表示为2n+1（n为整数）！！
例4.请对代数式a+2的实际意义作出解释。 解（1 ）某班原有学生a人，本学期又转来2人。
本学期这个班共有学生(a+2人) 解（2 ）一个圆的半径为a厘米，将半径增加2
厘米，圆的半径为(a+2)厘米。 你还能做出什么解释？
组内交流。
1.某地区夏季高山上的温度从山脚处开始每升 高100米降低0.7oC。如果山脚温度是28oC，那么山上300米处的温度为________一般地，山上x米处的温度为_____________.
2.学校体育器材室共有a个篮球，排球的数量比篮球数量的2倍少1个，排球共有______个；
3. ⑴ 一个两位数的个位数字是a，十位数字是b，这个两位数可表示为 ；
⑵ 如何用代数式表示一个三位数？
4.（1） a、b两数的平方和减去他们乘积的2倍；
（2） a、b两数的和的平方减去他们的差的平方；
（3） a、b两数的和与他们的差的乘积25.9oC(28—0.7x)oC10b+a2a-11、什么是代数式？怎么书写？2．怎样列代数式？
3．列代数式的关键是什么？
对于较复杂的数量关系，应按下述规律列代数式：
(1)列代数式，要以不改变原题叙述的数量关系为准(代数式的形式不唯一)；
(2)要善于把较复杂的数量关系，分解成几个基本的数量关系；
(3)把用日常生活语言叙述的数量关系，列成代数式，是为今后学习列方程解应用题做准备．要求学生一定要牢固掌握．
今天这节课，我们有哪些收获？
1、用代数式表示：
(1)体校里男生人数占学生总数的60%，女生人数是a，学生总数是多少？
(2)体校里男生人数是x，女生人数是y，教练人数与学生人数之比是1：10，教练人数是多少？
2、已知一个长方形的周长是24厘米，一边是a厘米，
求：(1)这个长方形另一边的长；
(2)这个长方形的面积．
3、对代数式a+b的实际意义作出解释。
4、课本第108页B组，2题和3题。
谢谢大家！！