§5.9.1实数

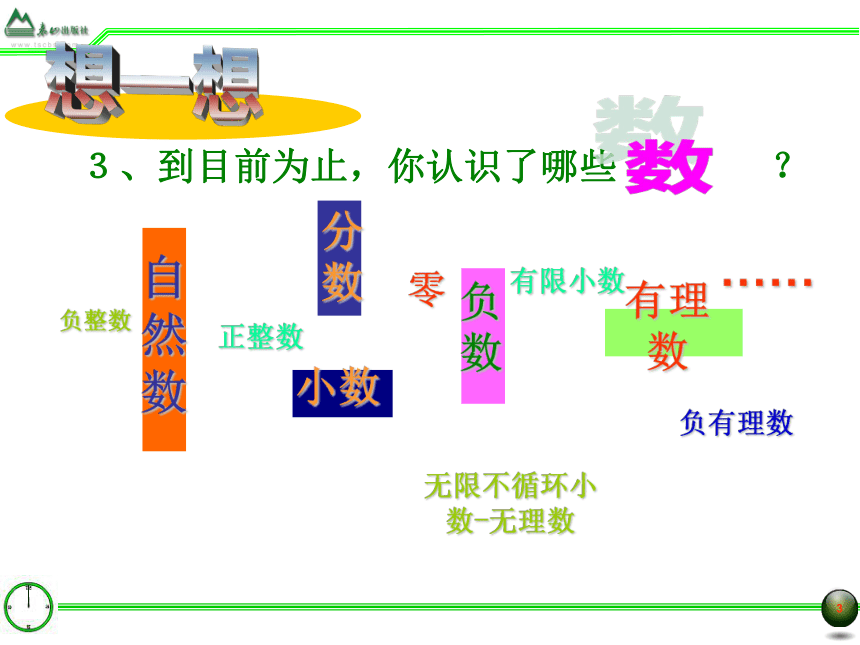
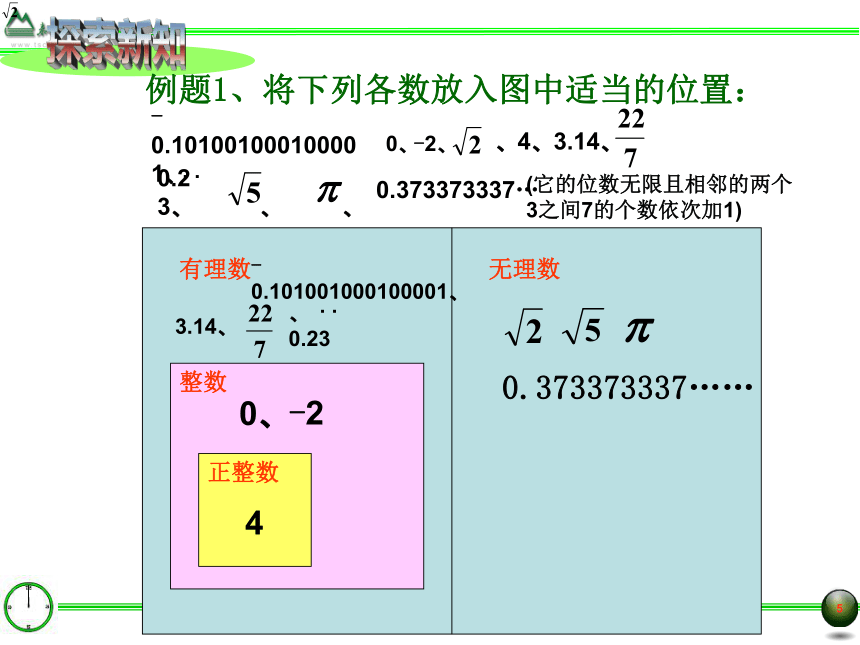
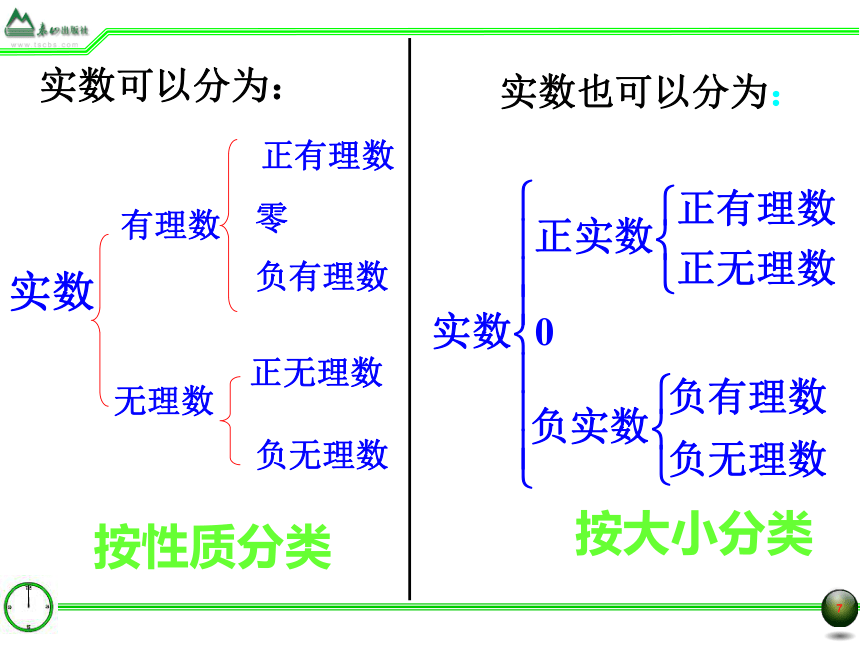
课件21张PPT。§5.9实数第五章：实数想一想自然数 分数负数 有理数 小数负整数 正整数 零 有限小数 无限不循环小数-无理数负有理数 …… 想一想以生命为代价de发现　　　毕达哥拉斯（Pythagoras）学派 “万物皆为数”（指有理数） 希帕斯（Hippasus）发现了一种实际存在的量，却不能表示为两个整数的比 这意味着什么？ 0.23、 、 、探索新知例题1、将下列各数放入图中适当的位置： -0.101001000100001、　 、 4、 3.14、0.373373337……40、-2-0.101001000100001、3.14、0.373373337…(它的位数无限且相邻的两个3之间7的个数依次加1)0、-2、. .无限不循环的小数无理数：实数也可以分为： 实数有理数无理数正有理数零负有理数正无理数负无理数实数可以分为：按性质分类按大小分类
例如：圆周率 及一些含有 的数都是无理数
像 的数是无理数。
有一定的规律，但不循环的无限小数都是无理数。例如：
0.1010010001…〔两个1之间依次多1个0〕
—234.232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
探索新知例题2 判断下列说法是否正确，并说明理由：练一练1、试一试：把下面实数的分类图填写完整： 实数整数无理数有理数（无限不循环小数）（q=1）（q≠1）分数自然数负整数（p≥0）（p＜0）练一练2、你能写出在4和5之间的一个无理数吗？ 你能写多少个？和你的同伴交流一下吧！写出十个数，包括有理数
和无理数。你来当老师练习1、在下列数中： 负有理数是：________________
正无理数是：___________________________
, ,练习2、填空：
（1） 的相反数是__________
（2） 的相反数是
（3） ___________
（4）绝对值等于 的数是 _________ 在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。议一议你能在数轴上表示 ?实数和数轴上的点是一一对应的。小结： 这节课你有什么收获？作业：习题5.9 T1,2,3；