9.2 30°、45°、60°角的三角比
文档属性
| 名称 | 9.2 30°、45°、60°角的三角比 |

|
|
| 格式 | rar | ||
| 文件大小 | 208.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-24 00:00:00 | ||
图片预览



文档简介
课件12张PPT。§9.2 30°、45°、60°角的三角比第9章 解直角三角形温故知新1. ∠ A的正弦:∠A的余弦:∠A的正切:锐角A的正弦、余弦、正切统称锐角A的三角比.2.一个锐角的三角比只与它的大小有关.实验与探究(1)sin45°,cos45 °,tan45 °的值分别是多少?在Rt△ABC中,∠C=90°, ∠A=45° .
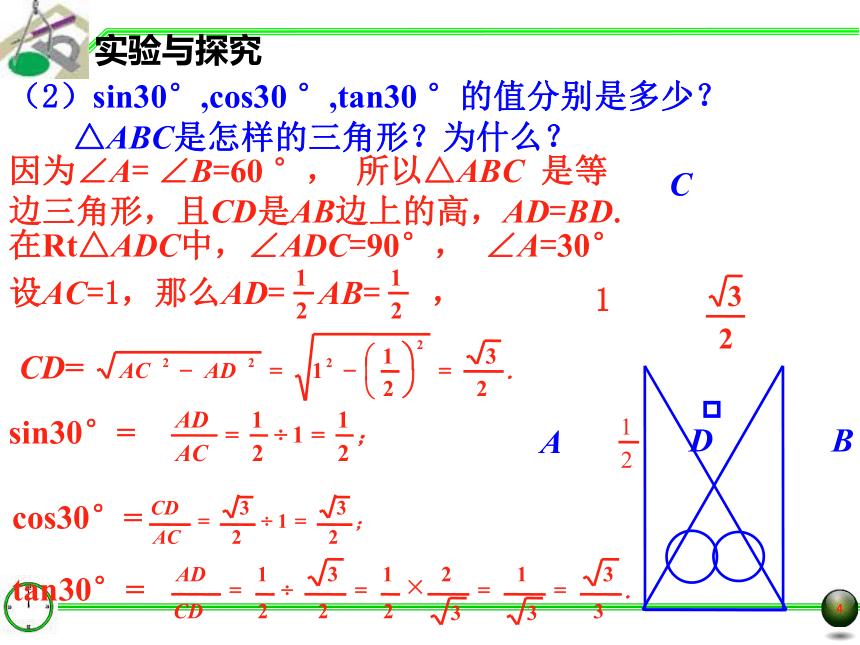
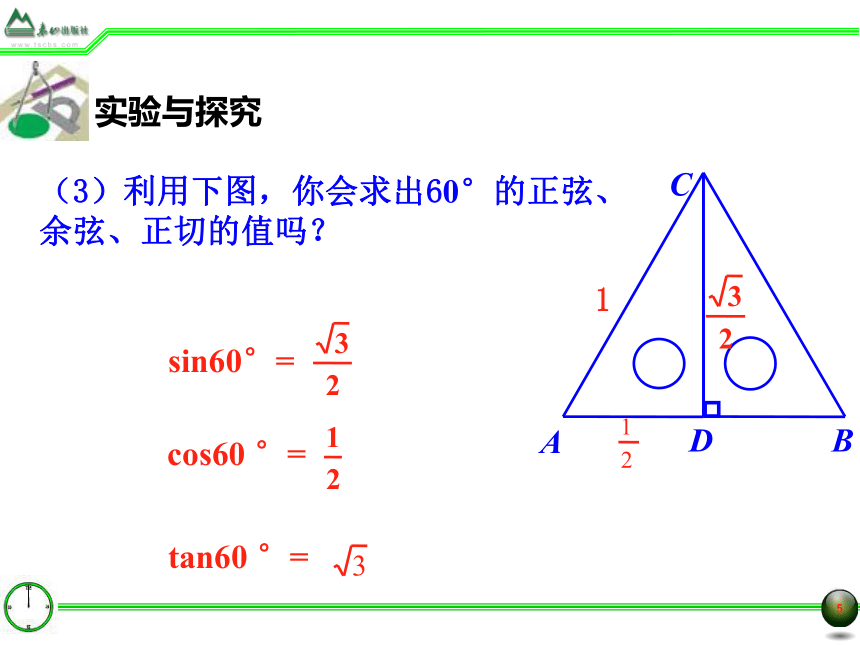
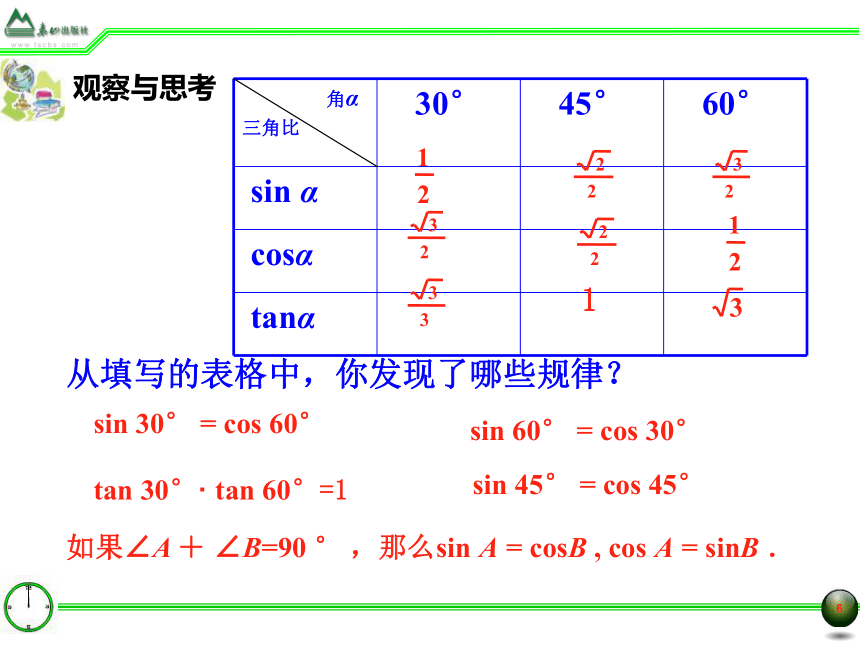
设AC=1,那么BC=AC=1,所以11实验与探究(2)sin30°,cos30 °,tan30 °的值分别是多少?在Rt△ADC中,∠ADC=90°, ∠A=30°1△ABC是怎样的三角形?为什么?因为∠A= ∠B=60 °, 所以△ABC 是等边三角形,且CD是AB边上的高,AD=BD.1实验与探究(3)利用下图,你会求出60°的正弦、余弦、正切的值吗?观察与思考1从填写的表格中,你发现了哪些规律?sin 30° = cos 60°sin 60° = cos 30°tan 30°· tan 60°=1 sin 45° = cos 45°如果∠A + ∠B=90 ° ,那么sin A = cosB , cos A = sinB .例题讲解例1求下列各式的值:
(1)sin30°·cos45° (2)tan45 °-cos60°.当A,B都是锐角时,如果sinA=sinB或cosA=cosB或tanA=tanB,那么A=B 如图,作边长为1 的正方形ABCD .延长边CB 到D ′ ,使B D ′= B D,连接D D ′ .你能利用这个图形求出22 . 5°角的正切的值吗?试一试.(1)sin30°-cos30°=________; (2) ·tan60 °=_____.(1)sin30°+cos60°; (2)tan30 °· tan60 °;
(3) 2sin60°- tan30 °;(4) sin45°· cos45°+ tan45 °.2.求下列各式的值:1.求下列各式的值:(1)1;(2)1;如果∠A + ∠B=90 ° ,那么sin A = cosB , cos A = sinB .1.特殊角的三角函数.2.已知特殊三角函数值,会求特殊角.1课堂小结作业必做题:课本P68 A组 1、2题
选做题:课本P68 B组 1、2、3、4题同学们,
再见!
设AC=1,那么BC=AC=1,所以11实验与探究(2)sin30°,cos30 °,tan30 °的值分别是多少?在Rt△ADC中,∠ADC=90°, ∠A=30°1△ABC是怎样的三角形?为什么?因为∠A= ∠B=60 °, 所以△ABC 是等边三角形,且CD是AB边上的高,AD=BD.1实验与探究(3)利用下图,你会求出60°的正弦、余弦、正切的值吗?观察与思考1从填写的表格中,你发现了哪些规律?sin 30° = cos 60°sin 60° = cos 30°tan 30°· tan 60°=1 sin 45° = cos 45°如果∠A + ∠B=90 ° ,那么sin A = cosB , cos A = sinB .例题讲解例1求下列各式的值:
(1)sin30°·cos45° (2)tan45 °-cos60°.当A,B都是锐角时,如果sinA=sinB或cosA=cosB或tanA=tanB,那么A=B 如图,作边长为1 的正方形ABCD .延长边CB 到D ′ ,使B D ′= B D,连接D D ′ .你能利用这个图形求出22 . 5°角的正切的值吗?试一试.(1)sin30°-cos30°=________; (2) ·tan60 °=_____.(1)sin30°+cos60°; (2)tan30 °· tan60 °;
(3) 2sin60°- tan30 °;(4) sin45°· cos45°+ tan45 °.2.求下列各式的值:1.求下列各式的值:(1)1;(2)1;如果∠A + ∠B=90 ° ,那么sin A = cosB , cos A = sinB .1.特殊角的三角函数.2.已知特殊三角函数值,会求特殊角.1课堂小结作业必做题:课本P68 A组 1、2题
选做题:课本P68 B组 1、2、3、4题同学们,
再见!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
