10.3方差与标准差（1）

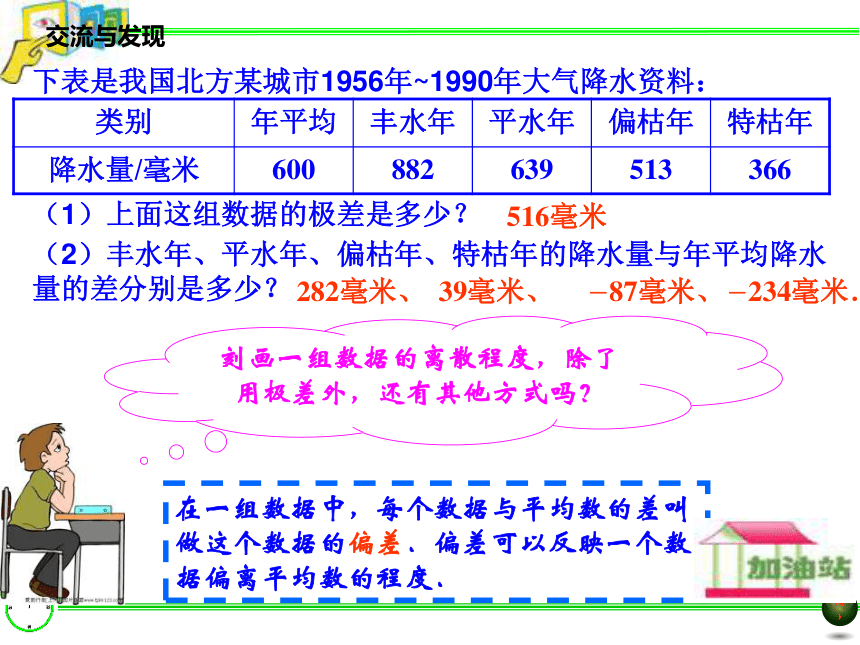
课件14张PPT。§10.3 方差与标准差（1）第10章 数据离散程度的度量温故知新1.一组数据中的最大数据与最小数据的差称为极差，即极差＝最大数据一最小数据．2.极差反映一组数据的波动范围，用极差描述这组数据的离散程度简单明了．极差越大，数据的离散程度越大．3.由于极差忽视了一组数据中所有数据之间的差异，仅仅由其中的最大值和最小值所确定，个别远离群体的极端值在很大程度上会影响极差，因而极差往往不能充分反映一组数据的实际离散程度．下表是我国北方某城市1956年~1990年大气降水资料：（1）上面这组数据的极差是多少？（2）丰水年、平水年、偏枯年、特枯年的降水量与年平均降水量的差分别是多少？在一组数据中，每个数据与平均数的差叫做这个数据的偏差．偏差可以反映一个数据偏离平均数的程度．刻画一组数据的离散程度，除了用极差外，还有其他方式吗？516毫米282毫米、39毫米、－87毫米、－234毫米．能用偏差的和表示一组数据的离散程度吗？282 ＋39 ＋（－87 ）＋（－234）=0 丰水年、平水年、偏枯年、特枯年的降水量与年平均降水量的差分别是282毫米、 39毫米、 － 87毫米、 －234毫米. 这是不是偶然现象呢？=0 为了刻画一组数据的离散程度，通常选用偏差的平方的平均数来描述． 由于偏差可能是正数、零、负数，在求偏差的和时，正、负数恰好相互抵消，结果为零,所以不能用偏差的和表示一组数据的离散程度. 在一组数据中，各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差（variance ) ，通常用S2 表示，即……2222＋＋＋＋nS2=方差越小，这组数据的离散程度越小，数据就越集中，平均数代表性就越大.例1某足球队对运动员进行射点球成绩测试，每人每天射点球5次，在10天中，运动员大刚的进球个数分别是：
5 4 5 3 3 5 2 5 3 5
（1）求大刚进球个数的平均数；
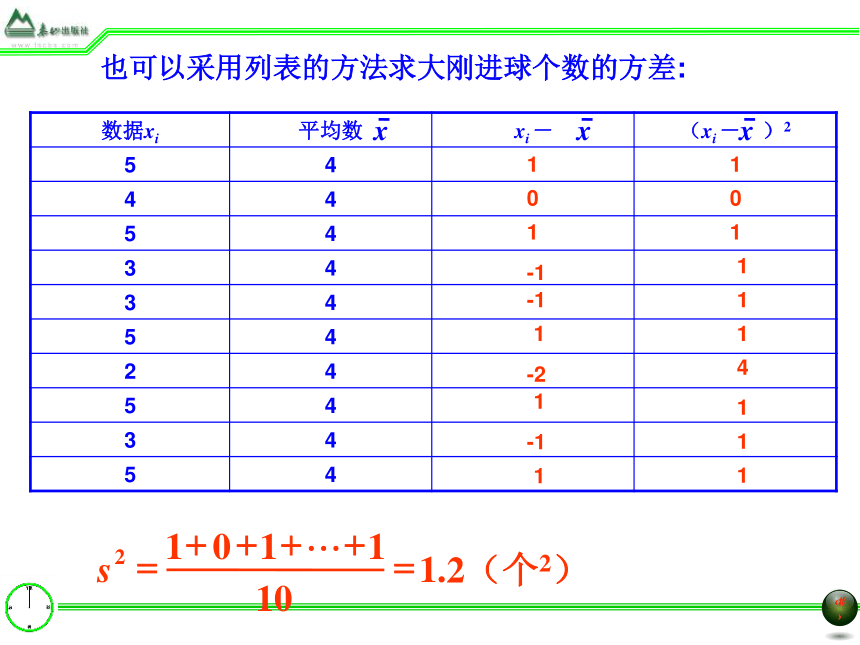
（2）求大刚进球个数的方差.解:（1）大刚进球个数的平均数为（2）大刚进球个数的方差为=1.2也可以采用列表的方法求大刚进球个数的方差:101-1-11-21-111011411111 由于方差S2的单位与原始数据单位不一致，因此在实际应用中常常求出方差后，再求它的算术平方根，这个算术平方根称为这组数据的标准差，用S表示.标准差也是表示一组数据离散程度的量.例1某足球队对运动员进行射点球成绩测试，每人每天射点球5次，在10天中，运动员大刚的进球个数分别是：
5 4 5 3 3 5 2 5 3 5
（1）求大刚进球个数的平均数；
（2）求大刚进球个数的方差.解:（1）大刚进球个数的平均数为（2）大刚进球个数的方差为=1.2（3）求大刚进球个数的标准差.（3）大刚进球个数的标准差为例题讲解1.八年级一班10 名同学参加用电脑绘图测试，成绩如下（满分30 分）:2 ．甲、乙两台编织机同时编织同种品牌的毛衣，在5 天中，两台编织机每天编织的合格产品数量如下（单位：件）: 甲：10 8 7 7 8 乙： 9 8 7 7 9 在这5 天中，哪台编织机每天编织的合格产品的数量较稳定？这10 名同学测试成绩的标准差是多少（精确到0 . 1 分）?解：平均分为：因为S甲＞S乙，所以乙编织机每天编织的合格产品的数量较稳定.1.在一组数据中，每个数据与平均数的差叫做这个数据的偏差．偏差可以反映一个数据偏离平均数的程度．由于偏差可能是正数、零、负数，在求偏差的和时，正、负数恰好相互抵消，结果为零,所以不能用偏差的和表示一组数据的离散程度.2. 在一组数据中，各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差，通常用S2 表示，即方差越小，这组数据的离散程度越小，数据就越集中，平均数代表性就越大.3.标准差:标准差也是表示一组数据离散程度的量.课堂小结作业必做题:课本P104 A组 1、2题
选做题:课本P104 B组 1题同学们,
再见!