2009---2010高作中学八年级第二学期期末复习章节知识整理
文档属性
| 名称 | 2009---2010高作中学八年级第二学期期末复习章节知识整理 |
|
|
| 格式 | rar | ||
| 文件大小 | 69.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-25 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2009---2010高作中学八年级第二学期期末复习章节知识整理
第一章 轴对称图形
1、
2、 轴对称图形
轴对称图形 线段 角 等腰三角形 等边三角形 等腰梯形
对称轴条数 2 1 1 3 1
对称轴名称
3、 重点图形
定义 性质 条件 基本图形 应用举例
垂直平分线 1 1 1
角平分线 1 1 1
等腰三角形 1 2 1
等边三角形 1 2 3
直角三角形 1 3+1 1+1
等腰梯形 1 2 1
4、典型图形
( http: / / www.21cnjy.com )
5、典型问题摘抄
第二章 勾股定理与平方根
1、
2、
3、
4、 典型图形
5、 典型问题摘抄
1 折叠问题
2 面积问题(割补法)
3 斜边得高(母子图)
4 断杆问题
1、 平方根(a≥0)
①正数有两个平方根,他们互为相反数
②0有1个平方根,就是0
③负数没有平方根
2、 算术平方根联想到
3、 负的平方根(算术平方根的相反数)
4、 算术平方根的性质
5、 立方根
1 正数的立方根是正数
2 负数的立方根是负数
3 0的立方根是0
6、 立方根的性质
7、 实数
8、 无理数比较大小一般采用平方法、估算法
9、 近似数
①科学记数法 把一个数记成的形式,其中1≤<10,n为整数
②有效数字(注意使用科学记数法)
③精确到×位(科学记数法先化为原数)
10、 数轴
①三要素 原点、正方向、单位长度
②
③如何读数轴 大小 绝对值大小
④两点间距离
11、 应用题注意点
1 符号意义的识别: HYPERLINK " http://www.21cnjy.com" EMBED Equation.3
2 生活实际问题中常见的方根模型(面积、体积、勾股定理)
3 计算得条理性和预见性
12、典型问题摘抄
第三章 中心对称图形
1、2、
3、中心对称图形
图形 平行四边形 矩形 菱形 正方形 三角形中位线 梯形中位线
对称中心 对角线交点
定义 1 1 1 1 1 1
性质 边 1 1 1 1 1
角 1 1 1
对角线 1 1 2 3
判定 边 2 1 既是矩形又是菱形
角 1
对角线 1 1 1
基本图形
应用举例
4、典型图形
5、典型问题摘抄
第四章 数量、位置的变化
1、 坐标系内点的特征:
名称 坐标特点
第一象限 (+,+)
第二象限 (-,+)
第二象限 (-,-)
第四象限 (+,-)
x轴 (x,0)
y轴 (0,y)
原点 (0,0)
2、 距离
①点p(x,y)到x轴的距离是;
②点p(x,y)到y轴的距离是;
③水平距离、铅直距离、到原点的距离
如图,OP=,AB=|d-e|,MN=|m-q|。
3、对称
①点p(a,b)到x轴的对称点是p1(a,-b);
②点p(a,b)到y轴的对称点是p2(-a,b);
③点p(a,b)关于原点的对称点是p3(-a,-b);
④关于x轴平行线对称 距离相等
⑤关于y轴平行线对称 距离相等
⑥关于任意点对称 中点
4、平移
5、点坐标求法
①平移法(求距离)
6、面积
7、典型问题摘抄
第五章 一次函数
1.
2、一次函数概念表示法
3、性质
①k>0图象经过一、三象限,y 随X的增大而增大
K<0图象经过二、四象限,y 随X的增大而减小
②b>0时,一次函数y=kx+b与y轴交于正半轴,图象经过一、二象限
b=0时,一次函数y=kx+b与y轴交于原点,这时y 是x的正比例函数
b<0时,一次函数y=kx+b与y轴交于负半轴图象经过三、四象限
③交点与x轴(,0) 与y轴(0,b)
3、点坐标求法
4、 求解析式
(1)数量关系列
(2)待定系数法
①设:根据条件,抓住特征设好解析式
②列:列方程或方程组
③解:解方程或方程组
④代:代入所设解析式中
(3)由k、b实际意义去求[]
(4)平移
(5)对称法
(6)由二元一次方程变
5、面积
①画图
②面积公式
③找底和高(水平方向或竖直方向,找不到用分割法)
④点坐标(不好求是就设)
6、生活实际应用题
①
②确定变量的含义
③图象横轴、纵轴的含义
④单位
⑤自变量的取值范围
7、一次函数几何应用题
线段长
典型问题摘抄
第六章数据的集中程度
1、
2、典型问题摘抄
七、一元一次不等式(组)
1、不等式性质:与等式性质作比较
①如果a>b,那么a+c>b+c,a-c>b-c;
②如果a>b,且c>0,那么ac>bc;
③如果a>b,且c<0,那么ac3、不等式的解(集)
4、解法步骤
序号 步骤 注意点
1 去分母 最小公倍数、漏乘
2 去括号 变号
3 移项 变号尽量使未知数的系数为正、变号
4 合并同类项 尽可能与移项同时进行
5 系数化为1 ①除以未知数的系数(乘以倒数)②注意系数为负时改变不等号方向
5、一元一次不等式组解法步骤
①分别解一元一次不等式
6、纯数学内应用题
(1)步骤
①找不等式模型(关键字词)
②问题的转化
(2)典型问题摘抄
5、实际情景应用题
(1)步骤
①审
②
③列
④解
⑤答 注意隐含条件
(2)常见问题类型:
做服装
装水果
山高与气温
第八章 分式
1、 分式定义
B=0时,分式无意义;B≠0时,分式有意义
2、分式值———为零:A=0且B≠0
3、分式基本性质
(1)基本性质①=(B≠0,M是不等于0的整式)
②=(B≠0,M是不等于0的整式)
(2)符号
4、乘除(本质是约分)
(1)法则
(2)步骤
①定符号
②约分→积的形式→因式分解→化去相同因式(顺序是数字、单个字母、多项式) →最简分式
③划 数、字母、多项式
5、加减法
(1)法则
①同分母分式的加减:±=
②异分母分式的加减:±=;
(2)步骤
②分子相加减
③约分
6、混合运算(计算步骤的清晰性、计算结果的预见性)
①看 运算符、括号、几段
②想 法则、简便计算(连加减、连乘除、乘法分配律、乘法公式顺逆使用)、个人注意点
③定 定顺序、分段定符号、定绝对值
④查 做一步查一步
7、典型问题摘抄
分式方程
1、解法
①在分式方程的两边同乘以最简公分母,化去分母,化成整式方程;
②解这个整式方程;
③验根。在方程变形时,有时可能产生不适合原方程的根,这种根叫做原方程的增根。
2、增根
使整式方程成立而分式方程无意义的未知数的值
3、 生活实际应用题
(1)应用步骤
①审 找题中基本数量关系,用适当名称给数量关系分类
②设 不好想时就设,问什么设什么
③列 纵向寻找同类数量关系列方程,以用过的数量关系不可以列方程
④解
⑤验 看根是否满足题意
⑥答
(2)典型问题摘抄
4、典型问题摘抄
解分式方程
增根本源
分式方程应用
第九章 反比例函数
1、定义:①
②Xy=k
③ 双曲线
2、反比例函数的性质
(1)图象:双曲线
(2)k的性质:
①当k>0时,第一、三象限,在每个象限内,y随x的增大而减小。
②当k<0时,第二、四象限,在每个象限内,y随x的增大而增大。
③不同象限,根据图象解决
(3)与x、y轴的关系 无限接近,永不相交
(4)中心对称、轴对称
3、点坐标求法
4、求解析式
①待定系数法
②数量关系列
③平移
④K的意义(总量)
⑤面积k=xy
5、面积:
①画图
②面积公式
③
④(不好求是就设)
⑤书写面积关系、计算公式、代入数据进行计算
⑥反比例函数中特殊面积关系的转换xy = k
⑦注意多解
6、生活实际应用题
①解析式
②确定变量的含义
③图象横轴、纵轴的含义
④单位
⑤自变量的取值范围(隐含条件的挖掘)
第十章 图形的相似知识结构图
1、
2、
定义 性质 判定
相似三角形 2 2 3
基本图形
应用举例
3、典型图形
4、典型问题摘抄
4、位似
第十一章 图形与证明(一)
1、
2、
图形 定义 性质 判定 基本图形 应用举例
三角形内角 1
三角形外角 2
平行线 3 3
角平分线
垂直
3、典型图形
4、典型问题摘抄
第十二章 认识概率
1、知识结构
2、典型问题摘抄
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2009---2010高作中学八年级第二学期期末复习章节知识整理
第一章 轴对称图形
1、
2、 轴对称图形
轴对称图形 线段 角 等腰三角形 等边三角形 等腰梯形
对称轴条数 2 1 1 3 1
对称轴名称
3、 重点图形
定义 性质 条件 基本图形 应用举例
垂直平分线 1 1 1
角平分线 1 1 1
等腰三角形 1 2 1
等边三角形 1 2 3
直角三角形 1 3+1 1+1
等腰梯形 1 2 1
4、典型图形
( http: / / www.21cnjy.com )
5、典型问题摘抄
第二章 勾股定理与平方根
1、
2、
3、
4、 典型图形
5、 典型问题摘抄
1 折叠问题
2 面积问题(割补法)
3 斜边得高(母子图)
4 断杆问题
1、 平方根(a≥0)
①正数有两个平方根,他们互为相反数
②0有1个平方根,就是0
③负数没有平方根
2、 算术平方根联想到
3、 负的平方根(算术平方根的相反数)
4、 算术平方根的性质
5、 立方根
1 正数的立方根是正数
2 负数的立方根是负数
3 0的立方根是0
6、 立方根的性质
7、 实数
8、 无理数比较大小一般采用平方法、估算法
9、 近似数
①科学记数法 把一个数记成的形式,其中1≤<10,n为整数
②有效数字(注意使用科学记数法)
③精确到×位(科学记数法先化为原数)
10、 数轴
①三要素 原点、正方向、单位长度
②
③如何读数轴 大小 绝对值大小
④两点间距离
11、 应用题注意点
1 符号意义的识别: HYPERLINK " http://www.21cnjy.com" EMBED Equation.3
2 生活实际问题中常见的方根模型(面积、体积、勾股定理)
3 计算得条理性和预见性
12、典型问题摘抄
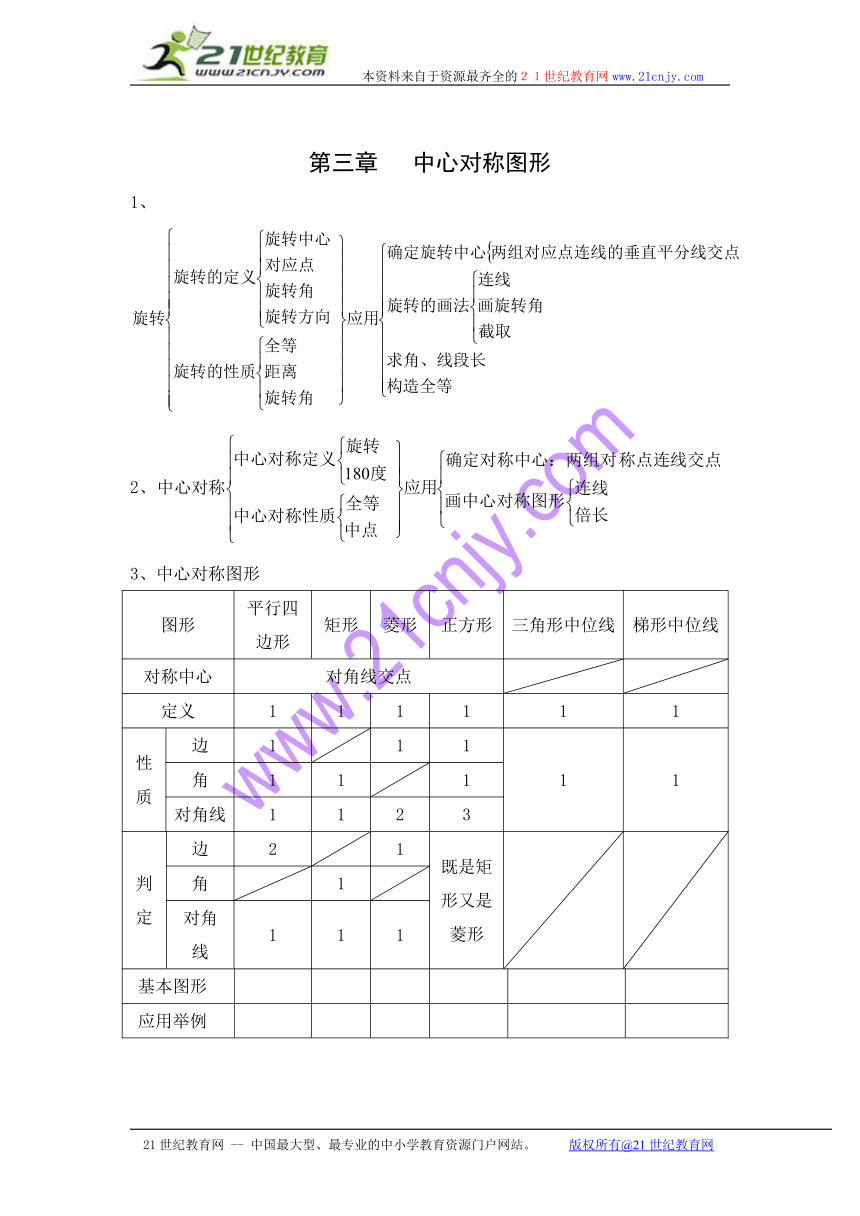
第三章 中心对称图形
1、2、
3、中心对称图形
图形 平行四边形 矩形 菱形 正方形 三角形中位线 梯形中位线
对称中心 对角线交点
定义 1 1 1 1 1 1
性质 边 1 1 1 1 1
角 1 1 1
对角线 1 1 2 3
判定 边 2 1 既是矩形又是菱形
角 1
对角线 1 1 1
基本图形
应用举例
4、典型图形
5、典型问题摘抄
第四章 数量、位置的变化
1、 坐标系内点的特征:
名称 坐标特点
第一象限 (+,+)
第二象限 (-,+)
第二象限 (-,-)
第四象限 (+,-)
x轴 (x,0)
y轴 (0,y)
原点 (0,0)
2、 距离
①点p(x,y)到x轴的距离是;
②点p(x,y)到y轴的距离是;
③水平距离、铅直距离、到原点的距离
如图,OP=,AB=|d-e|,MN=|m-q|。
3、对称
①点p(a,b)到x轴的对称点是p1(a,-b);
②点p(a,b)到y轴的对称点是p2(-a,b);
③点p(a,b)关于原点的对称点是p3(-a,-b);
④关于x轴平行线对称 距离相等
⑤关于y轴平行线对称 距离相等
⑥关于任意点对称 中点
4、平移
5、点坐标求法
①平移法(求距离)
6、面积
7、典型问题摘抄
第五章 一次函数
1.
2、一次函数概念表示法
3、性质
①k>0图象经过一、三象限,y 随X的增大而增大
K<0图象经过二、四象限,y 随X的增大而减小
②b>0时,一次函数y=kx+b与y轴交于正半轴,图象经过一、二象限
b=0时,一次函数y=kx+b与y轴交于原点,这时y 是x的正比例函数
b<0时,一次函数y=kx+b与y轴交于负半轴图象经过三、四象限
③交点与x轴(,0) 与y轴(0,b)
3、点坐标求法
4、 求解析式
(1)数量关系列
(2)待定系数法
①设:根据条件,抓住特征设好解析式
②列:列方程或方程组
③解:解方程或方程组
④代:代入所设解析式中
(3)由k、b实际意义去求[]
(4)平移
(5)对称法
(6)由二元一次方程变
5、面积
①画图
②面积公式
③找底和高(水平方向或竖直方向,找不到用分割法)
④点坐标(不好求是就设)
6、生活实际应用题
①
②确定变量的含义
③图象横轴、纵轴的含义
④单位
⑤自变量的取值范围
7、一次函数几何应用题
线段长
典型问题摘抄
第六章数据的集中程度
1、
2、典型问题摘抄
七、一元一次不等式(组)
1、不等式性质:与等式性质作比较
①如果a>b,那么a+c>b+c,a-c>b-c;
②如果a>b,且c>0,那么ac>bc;
③如果a>b,且c<0,那么ac
4、解法步骤
序号 步骤 注意点
1 去分母 最小公倍数、漏乘
2 去括号 变号
3 移项 变号尽量使未知数的系数为正、变号
4 合并同类项 尽可能与移项同时进行
5 系数化为1 ①除以未知数的系数(乘以倒数)②注意系数为负时改变不等号方向
5、一元一次不等式组解法步骤
①分别解一元一次不等式
6、纯数学内应用题
(1)步骤
①找不等式模型(关键字词)
②问题的转化
(2)典型问题摘抄
5、实际情景应用题
(1)步骤
①审
②
③列
④解
⑤答 注意隐含条件
(2)常见问题类型:
做服装
装水果
山高与气温
第八章 分式
1、 分式定义
B=0时,分式无意义;B≠0时,分式有意义
2、分式值———为零:A=0且B≠0
3、分式基本性质
(1)基本性质①=(B≠0,M是不等于0的整式)
②=(B≠0,M是不等于0的整式)
(2)符号
4、乘除(本质是约分)
(1)法则
(2)步骤
①定符号
②约分→积的形式→因式分解→化去相同因式(顺序是数字、单个字母、多项式) →最简分式
③划 数、字母、多项式
5、加减法
(1)法则
①同分母分式的加减:±=
②异分母分式的加减:±=;
(2)步骤
②分子相加减
③约分
6、混合运算(计算步骤的清晰性、计算结果的预见性)
①看 运算符、括号、几段
②想 法则、简便计算(连加减、连乘除、乘法分配律、乘法公式顺逆使用)、个人注意点
③定 定顺序、分段定符号、定绝对值
④查 做一步查一步
7、典型问题摘抄
分式方程
1、解法
①在分式方程的两边同乘以最简公分母,化去分母,化成整式方程;
②解这个整式方程;
③验根。在方程变形时,有时可能产生不适合原方程的根,这种根叫做原方程的增根。
2、增根
使整式方程成立而分式方程无意义的未知数的值
3、 生活实际应用题
(1)应用步骤
①审 找题中基本数量关系,用适当名称给数量关系分类
②设 不好想时就设,问什么设什么
③列 纵向寻找同类数量关系列方程,以用过的数量关系不可以列方程
④解
⑤验 看根是否满足题意
⑥答
(2)典型问题摘抄
4、典型问题摘抄
解分式方程
增根本源
分式方程应用
第九章 反比例函数
1、定义:①
②Xy=k
③ 双曲线
2、反比例函数的性质
(1)图象:双曲线
(2)k的性质:
①当k>0时,第一、三象限,在每个象限内,y随x的增大而减小。
②当k<0时,第二、四象限,在每个象限内,y随x的增大而增大。
③不同象限,根据图象解决
(3)与x、y轴的关系 无限接近,永不相交
(4)中心对称、轴对称
3、点坐标求法
4、求解析式
①待定系数法
②数量关系列
③平移
④K的意义(总量)
⑤面积k=xy
5、面积:
①画图
②面积公式
③
④(不好求是就设)
⑤书写面积关系、计算公式、代入数据进行计算
⑥反比例函数中特殊面积关系的转换xy = k
⑦注意多解
6、生活实际应用题
①解析式
②确定变量的含义
③图象横轴、纵轴的含义
④单位
⑤自变量的取值范围(隐含条件的挖掘)
第十章 图形的相似知识结构图
1、
2、
定义 性质 判定
相似三角形 2 2 3
基本图形
应用举例
3、典型图形
4、典型问题摘抄
4、位似
第十一章 图形与证明(一)
1、
2、
图形 定义 性质 判定 基本图形 应用举例
三角形内角 1
三角形外角 2
平行线 3 3
角平分线
垂直
3、典型图形
4、典型问题摘抄
第十二章 认识概率
1、知识结构
2、典型问题摘抄
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
