代数方程总复习
图片预览




文档简介
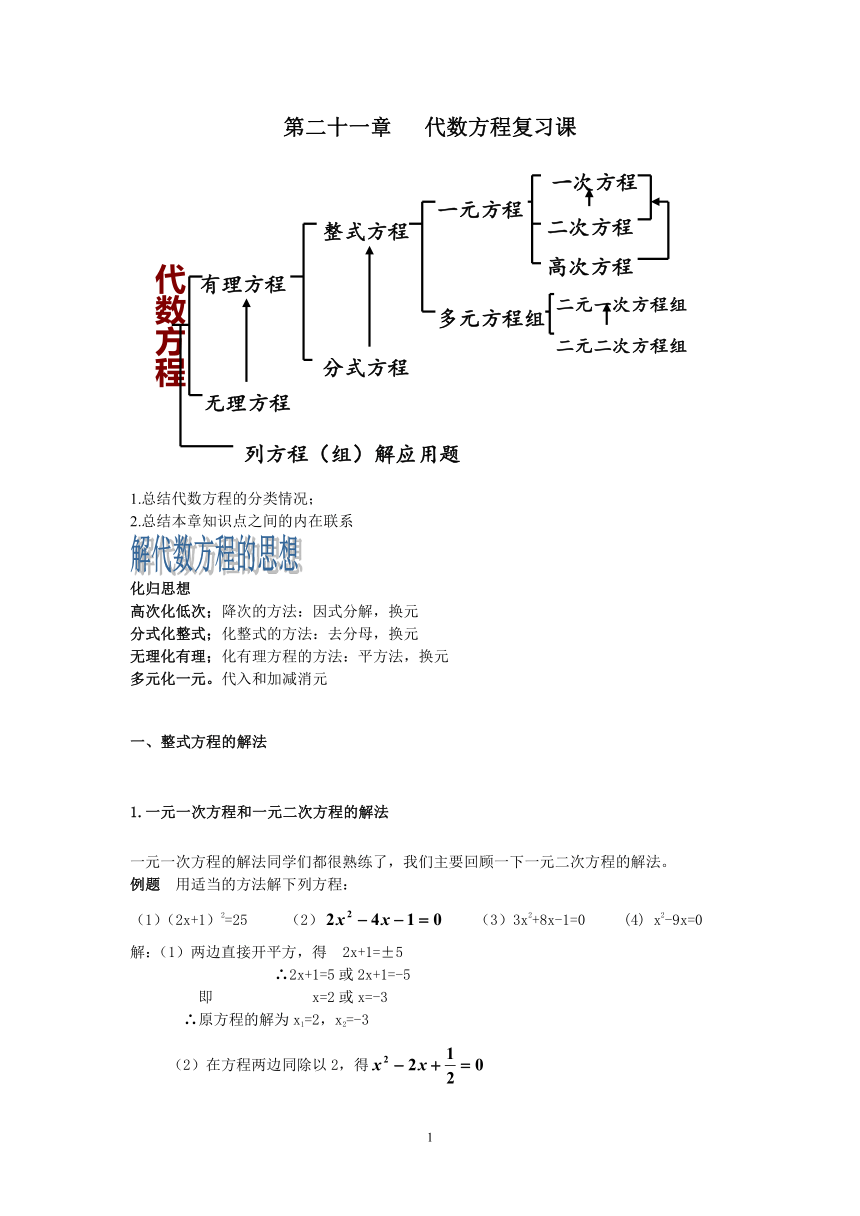
第二十一章 代数方程复习课
1.总结代数方程的分类情况;
2.总结本章知识点之间的内在联系
化归思想
高次化低次;降次的方法:因式分解,换元
分式化整式;化整式的方法:去分母,换元
无理化有理;化有理方程的方法:平方法,换元
多元化一元。代入和加减消元
一、整式方程的解法
1.一元一次方程和一元二次方程的解法
一元一次方程的解法同学们都很熟练了,我们主要回顾一下一元二次方程的解法。
例题 用适当的方法解下列方程:
(1)(2x+1)2=25 (2) (3)3x2+8x-1=0 (4) x2-9x=0
解:(1)两边直接开平方,得 2x+1=±5
∴2x+1=5或2x+1=-5
即 x=2或x=-3
∴原方程的解为x1=2,x2=-3
(2)在方程两边同除以2,得
移项,得
方程配方,得
即
利用直接开平方法,得
∴原方程的解为,
(3),
∴原方程有实数解。
∴,
(4)方程左边因式分解,得 x(x-9)=0
∴x1=0,x2=9
一元二次方程的解法主要有四种:
(1)直接开平方法:
适用于(mx+n)2=h (h≥0)的一元二次方程。
(2)配方法:
适用于所有化为一般形式后的一元二次方程。但是,具有二次项系数为1,一次项系数为偶数特点的一元二次方程,用配方法解才较简便。
配方法是通过配方将一元二次方程化成(mx+n)2=h (h≥0)的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法。
其基本步骤是:
①首先在方程两边同除以二次项系数,把二次项系数化为1;
②把常数项移到等式的右边;
③方程两边同时加上一次项系数一半的平方;
④方程左边写成完全平方式,右边化简为常数;
⑤利用直接开平方法解此方程
用配方法解一元二次方程要注意,当二次项系数不为1时,一定要化为1,然后才能方程两边同时加上一次项系数一半的平方
(3)公式法:
适用于解一般形式的一元二次方程。利用公式可以解所有的一元二次方程。
注意:当b2-4ac≥0时,方程才有实数解;当b2-4ac<0时,原方程无实数解。
(4)因式分解法:
适用于方程右边是0,左边是易于分解成两个一次因式乘积的一元二次方程。
2.含字母系数的整式方程的解法
例题 解下列关于x的方程
(1)(3a-2)x=2(3-x)
(2)bx2-1=1-x2(b≠-1)
解(1)去括号,得 3ax-2x=6-2x
移项,得 3ax-2x+2x=6
合并同类项,得 3ax=6 ※
当a≠0时,方程※是一元一次方程,解得 ;
当a=0时,方程※变成 0·x=6,这时不论x取什么值,等式0·x=6都不成立,因此方程无解。
所以,当a≠0时,原方程的根是;当a=0时,原方程无解。
(2)移项,得 bx2+x2=1+1
合并同类项,得(b+1)x2=2
因为b≠-1,所以b+1≠0
两边同除以b+1,得 ※
当b+1>0时,由方程※解得 ;
当b+1<0时,方程※中,这时方程没有实数根。
所以,当b+1>0时,原方程的根是,;
当b+1<0时,原方程没有实数根。
3.特殊的高次方程的解法
(1)二项方程的解法
二项方程的定义:
如果一元n次方程的一边只有含未知数的一项和非零的常数项,另外一边是零,那么这样的方程叫做二项方程。
关于x的一元n次二项方程的一般形式是
二项方程的解法及根的情况:
一般地,二项方程可变形为
可见,解一元n次二项方程,可以转化为求一个已知数的n次方根,运用开方运算可以求出这个方程的根。
二项方程的根的情况:
对于二项方程,
当n为奇数时,方程只有且只有一个实数根。
当n为偶数时,如果,那么方程有两个实数根,且这两个实数根互为相反数;如果,那么方程没有实数根。
例题 判断下列方程是不是二项方程,如果是二项方程,求出它的根。
(1)x3-64=0 (2)x4+x=0
(3)x5= -9 (4)x3+x=1
解:(1)、(3)是二项方程,(2)、(4)不是二项方程。
下面解方程(1)、(3):
(1)移项,得 x3=64
开方,得
即 x=4
(3)开方,得
即
(2)双二次方程的解法
双二次方程的定义:
只含有偶数次项的一元四次方程,叫做双二次方程。
关于x的双二次方程的一般形式是
双二次方程的解法:
可以用“换元法”解形如的双二次方程。就是用y代替方程中的x2,同时用y2代替x4,将方程转化为关于y的一元二次方程
ay2+by+c=0
解这个关于y的一元二次方程即可。
通过换元,把双二次方程转化为一元方程体现了“降次”的策略。
例题 判断下列方程是不是双二次方程,如果是,求出它的根:
(1)x4-9x2+14=0 (2)x4+10x+25=0
(3)2x4-7x3-4=0 (4)x4+9x2+20=0
解:(1)、(4)是双二次方程,(2)、(3)不是双二次方程。
下面解方程(1)、(4):
(1) 设x2=y,则x4=y2,于是原方程可化为
y2-9y+14=0
解这个关于y的方程,得
y1=2,y2=7
由y1=2,得x2=2,解得
由y2=7,得x2=7,解得
所以,原方程的根是
x1=,x2=,x3=,x4=
(4)设x2=y,则x4=y2,于是原方程可化为
y2+9y+20=0
解这个关于y的方程,得
y1=-4,y2=-5
由y1=-4,得x2=-4,它没有实数根;
由y2=-5,得x2=-5,它也没有实数根
所以,原方程没有实数根。
(3)因式分解法解高次方程
解高于一次的方程,基本思想就是是“降次”,对有些高次方程,可以用因式分解的方法降次。
用因式分解的方法时要注意:一定要使方程的一边为零,另一边可以因式分解。
例题 解下列方程:
(1)2x3+7x2-4x=0 (2)x3-2x2+x-2=0
解:(1)方程左边因式分解,得
x(2x2+7x-4)=0
x(x+4)(2x-1)=0
得x=0或x+4=0或2x-1=0
∴原方程的根是 x=0,x=-4,x=
注意:不要漏掉x=0这个根!
(2)方程左边因式分解,得
(x3-2x2) +(x-2)=0
x2(x-2)+(x-2)=0
(x-2)(x2+1)=0
即 x-2=0或x2+1=0
解方程x-2=0得 x=2
方程x2+1=0没有实数根
所以,原方程的根是 x=2
1. 字母系数方程的讨论
关于ax=b的解有三种情况
关于a=m的解的情况
解方程(1)
(2)
2、特殊高次方程的解法
一般地,二项方程可转化为,转化为求一个数的n次方根,解关于x的双二次方程换元法,y代替,转化为关于y的一元二次方程方程可转化为等号左边是多项式,右边是零。用因式分解的方法可得A·B=0从而转化成 A = 0或 B = 0
3、分式方程的解法
解分式方程的基本思路是:
去分母的关键是确定最简公分母,
在转化过程中要注意不要漏乘,不忘检验。
二、可化为一元二次方程的分式方程的解法
1.适宜用“去分母”的方法的分式方程
解分式方程,通常是通过方程两边同乘以方程中各分式的最简公分母,约去分母,化为整式方程来解。
解分式方程要注意验根!
例题 解下列方程
分析:本例是一道分式方程,通常采用去分母法。
(1)首先应观察各项分母,如能分解因式必须先分解因式,如本例x2-17x+60可分解因式为(x-5)(x-12).
(2)分解因式后再找各分母的最小公倍式.如本例为“(x-5)(x-12)”.
(3)用此整式去乘方程的每一项,便可约去分母,将分式方程转化为整式方程求解.
(4)最后应检验,至此例可找到本例完整解答.
解:原方程就是
,
方程两边都乘以,约去分母,得
,
整理后,得
.
解这个方程,得
.
检验:,
∴ 均为原方程根.
在去分母的过程中要注意两点:(1)必须注意符号的变化规律(如本例“12-x”与“x-12”的关系);(2)用整式乘以方程的每一项,一项都不能漏.
2.适宜用“换元法”的分式方程
适宜用换元法的分式方程有两种,一是二次项与一次项相同的,采取同底换元法;二是不看系数,方程的未知项呈倒数关系的,可采取倒数换元法,
下面的例题中的两个方程,分别具有这两种特点。
例题 解下列方程:
(1);
(2).
(1)分析:观察方程(1)可发现二次项底数与一次项未知底数相同,因而,可考虑同底换元法为宜.
解:(1)设.则原方程可化为
,
,
∴ .
当y1=-2时,即;
当y2=-3时,即.
∴ 均为原方程的根.
(2)分析:观察方程(2)可发现这个方程左边两个分式中的与互为倒数,根据这个特点,可以用倒数换元法来解.
解:设,那么,于是原方程变形为
,
去分母,得 ,
,
解得 y1=,y2=1.
当 y=时,.
去分母并整理,得
.
解得 .
当y=1时,即.
去分母并整理,得
.
检验:把分别代入原方程的分母,各分母都不等于0,所以它们都是原方程的根.
∴原方程根是:.
由此可以看出,解分式方程“转化”为整式方程(一元一次方程或一元二次方程)用去分母法是基础方法,解分式方程应首先考虑用基本方法求解,然后再根据分式方程特点,考虑换元法,便可达到转化的目的,找到思路.对于解题过程的每一个步骤都不能疏忽,才能正确求解.
4、用换元法解分式方程
1.原方程可看作某一分式的二次方程.
2.原方程含有未知数的几个分式有互为倒数的关系.
特别注意:换元法解分式方程需要验根两次
第1次检验y的方程是否有增根
第2次是回代后的关于x两个方程是否有增根
例题
解方程 时,设 y =________,
则原方程化为关于y 的整式方程是:____________________。
解方程:(4x+1)(3x+1)(2x+1)(x+1)=3
设:5x+1=a,
∴原方程的根是
5、无理方程的解法
代数式可分为有理式和无理式,有理式又可分为整式和分式。通过比较,我们可以看到代数式和实数分类结构相同,如下图所示∶
,
我们继续定义∶有理方程和无理方程统称代数方程。代数方程结构如下∶
无理方程的定义∶可写为含有未知数的方程叫做无理方程。
解无理方程的基本思路是把无理方程化为有理方程,通常采用“两边平方”的方法解。对有些特殊的无理方程,可以用“换元法”解。
解无理方程一定要验根!
在初中阶段,我们主要学习下面两种无理方程的解法。
1.只有一个含未知数根式的无理方程
当方程中只有一个含未知数的二次根式时,可先把方程变形,使这个二次根式单独在一边;然后方程的两边同时平方,将这个方程化为有理方程。
例题 解下列方程:
(1) (2)
解:(1)两边平方,得 4(x-3)=(x-6)2
整理,得 x2-16x+48=0
解这个方程,得 x1=4,x2=12
经检验,x=4是增根,舍去;x=12是原方程的根。
所以,原方程的根是 x=12
(2)原方程可变形为
两边平方,得 (3-x)2=2x-3
整理,得 x2-8x+12=0
解得 x1=2,x2=6
经检验,x=2是原方程的根;x=6是增根,舍去。
所以,原方程的根是x=2
2.有两个含未知数根式的无理方程
当方程中有两个含未知数的二次根式时,可先把方程变形,使乙个二次根式单独在一边,另外一个二次根式在方程的另一边;然后方程的两边同时平方,将这个方程化为有理方程。
例题 解下列方程:
(1) (2)
解:(1)原方程可变形为
两边平方,得 x2-2=2x+1
整理,得 x2-2x-3=0
解得 x1=-1,x2=3
经检验,x=-1是增根,舍去;x=3是原方程的根。
所以,原方程的根是 x=3
3.适宜用换元法解的无理方程
如果无理方程中,二次根式里面的未知项和二次根式外面的未知项相同,可以使用换元法来解。
例题 解方程
解:设=y,则3x2-6x+12=3y2 ,则3x2-6x=3y2-12
原方程化为 2y=3y2-12+4
整理,得 3y2-2y-8=0
解得 y1=2,y2=
当y=2时,=2,=4,解得x=0或x=2;
y=时,=,次方程无解。
经检验,x=0,x=2都是原方程的根。
所以,原方程的根是 x1=0,x2=2
解无理方程的一般步骤:
6、有关增根的问题
增根产生的原因:
在解分式方程或无理方程时,将方程转化成整式方程或
有理方程时,扩大了未知数的取值范围,从而产生了增根
如何检验是否增根
将解分式方程转化成整式方程的根代入最简公分母,若使最简公分母为零的根为原方程的增根,否则为原方程的根将解无理方程转化成有理方程的根代入原方程的左右两边,若使方程左右两边的值不相等的根为增根,否则为方程的根。
练习∶解无理方程∶
7、二元二次方程(组)
一、由一个二元一次方程和一个二元二次方程组成的方程组
代入消元法、因式分解降次法和利用根与系数关系
【例1】解方程组
分析:由于方程(1)是二元一次方程,故可由方程(1),得,代入方程(2)消去.
解:由(1)得: (3)
将(3)代入(2)得:,解得:
把代入(3)得:;把代入(3)得:.
∴原方程组的解是:.
说明:(1) 解由一个二元一次方程和一个二元二次方程组成的方程组的步骤:
①由二元一次方程变形为用表示的方程,或用表示的方程(3);
②把方程(3)代入二元二次方程,得一个一元二次方程;
③解消元后得到的一元二次方程;
④把一元二次方程的根,代入变形后的二元一次方程(3),求相应的未知数的 值;
⑤写出答案.
(2) 消,还是消,应由二元一次方程的系数来决定.若系数均为整数,那 么最好消去系数绝对值较小的,如方程,可以消去,变形 得,再代入消元.
(3) 消元后,求出一元二次方程的根,应代入二元一次方程求另一未知数的值, 不能代入二元二次方程求另一未知数的值,因为这样可能产生增根,这一点 切记.
【例2】解方程组
分析:本题可以用代入消元法解方程组,但注意到方程组的特点,可以把、看成是方程的两根,则更容易求解.
解:根据一元二次方程的根与系数的关系,把、看成是方程的两根,解方程得:.
∴ 原方程组的解是:.
说明:(1) 对于这种对称性的方程组,利用一元二次方程的根与系数的关系构造方程时,未知数要换成异于、的字母,如.
(2) 对称形方程组的解也应是对称的,即有解,则必有解.
课堂练习
二、由两个二元二次方程组成的方程组
1.可因式分解型的方程组
方程组中的一个方程可以因式分解化为两个二元一次方程,则原方程组可转化为两个方程组,其中每个方程组都是由一个二元二次方程和一个二元一次方程组成.
【例3】解方程组
分析:注意到方程,可分解成,即得或,则可得到两个二元二次方程组,且每个方程组中均有一个方程为二元一次方程.
解:由(1)得:
∴ 或
∴ 原方程组可化为两个方程组:
用代入法解这两个方程组,得原方程组的解是:
说明:由两个二元二次方程组成的方程组中,有一个方程可以通过因式分解,化为两个二元一次方程,则原方程组转化为解两个方程组,其中每一个方程组均有一个方程是二元一次方程.
【例4】解方程组
分析:本题的特点是方程组中的两个方程均缺一次项,我们可以消去常数项,可得到一个二次三项式的方程.对其因式分解,就可以转化为例3的类型.
解:(1) –(2)得:
即
∴
∴ 原方程组可化为两个二元一次方程组:.
用代入法解这两个方程组,得原方程组的解是:.
说明:若方程组的两个方程均缺一次项,则消去常数项,得到一个二元二次方程.此方程与原方程组中的任一个方程联立,得到一个可因式分解型的二元二次方程组.
【例5】解方程组
分析:(1) +(2)得:,(1) -(2)得:,分别分解(3)、(4)可得四个二元一次方程组.
解:(1) +(2)得:, (1) -(2)得:.
解此四个方程组,得原方程组的解是:
.
说明:对称型方程组,如、都可以通过变形转化为的形式,通过构造一元二次方程求解.
因式分解法
8、列方程(组)解应用题
1.解下列方程组:
(1) (2)
(3) (4)
2.解下列方程组:
(1) (2)
3.解下列方程组:
(1) (2)
(3) (4)
4.解下列方程组:
(1) (2)
1.在方程中,若设,则原方程化为关于y的方程
是 .
2.当m= 时,关于x的分式方程没有实数解.
3.若关于x的方程有实数根,则a的取值范围是 .
4.用换元法解方程时,可设 =y,这时原方程变为 .
5.方程的根是 ;的根是 ;的根
是 .
6.无理方程的根为,则a的值为 .
7.若a,b都是正实数,且,则 .
8.若a+b=1,且a∶b=2∶5,则2a-b= .
9.当a= 时,方程无实数根.
10.若,则 .
11.下列方程中既不是分式方程,也不是无理方程的有( )
A. B. C.
D. E. F.
12.方程的最简公分母是( )
A.24(x+3)(x-3) B.(x+3)(x-3)2 C.24(x+3)(x-3)2 D.12(x+3)(x-3)2
13.观察下列方程,经分析判断得知有实数根的是( )
A. B. C. D.
14.如果,那么的值是( )
A.1 B.-1 C.±1 D.4
15.方程的解是( )
A.0 B.2 C.0或2 D.
16.设y=x2+x+1,则方程可变形为( )
A.y2-y-2=0 B.y2+y+2=0 C.y2+y-2=0 D.y2-y+2=0
17.若,则a的取值范围是( )
A.全体实数 B.a≥0 C.a≥ D.A≤
18.已知,则相等关系成立的式子是( )
A. B. C. D.
19.关于x的方程的根是( )
A.x=a B.x=-a C.x1=a;x2=- D.x1=a;x2=
20.一个数和它的算术平方根的4倍相等,那么这个数是( )
A.0 B.16 C.0或16 D.4或16
21.; 22.;
23.; 24.;
25.; 26.
用方程解应用题
1、块面积相同的小麦试验田,第一块使用原品种,第二块使用新品种,分别收获小麦9000Kg和15000Kg,已知第一块试验田的每公顷的产量比第二块少3000Kg,分别求这块试验田每公顷的产量。
2、从甲地到乙地有两条公路:一条是全长600Km的普通公路,另一条是全长480Km的告诉公路。某客车在高速公路上行驶的平均速度比在普通公路上快45Km,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需要的时间。
3、从甲地到乙地的路程是15千米,A骑自行车从甲地到乙地先走,40分钟后,B骑自行车从甲地出发,结果同时到达。已知B的速度是A的速度的3倍,求两车的速度。
4、一台甲型拖拉机4天耕完一块地的一半,加一天乙型拖拉机,两台合耕,1天耕完这块地的另一半。乙型拖拉机单独耕这块地需要几天?
5、A做90个零件所需要的时间和B做120个零件所用的时间相同,又知每小时A、B两人共做35个机器零件。求A、B每小时各做多少个零件。
6、某工厂去年赢利25万元,按计划这笔赢利额应是去、今两年赢利总额的20%,今年的赢利额应是多少?
7、某农场原有水田400公顷,旱田150公顷,为了提高单位面积产量,准备把部分旱田改为水田,改完之后,要求旱田占水田的10%,问应把多少公顷旱田改为水田。
8、轮船顺水航行80千米所需要的时间和逆水航行60千米所用的时间相同。已知水流的速度是3千米/时,求轮船在静水中的速度。
二元二次方程组
二次方程
高次方程
一次方程
二元一次方程组
多元方程组
一元方程
分式方程
列方程(组)解应用题
无理方程
有理方程
整式方程
代数方程
使最简公分母不为零
写出方程的根
舍去
检验
整式方程
同乘以最简公分母
分式方程
解分式方程的一般步骤:
通过“去分母”将分式方程转化为整式方程
使最简公分母为零
增长率问题,工程问题,行程问题……
检验
结束
无理方程有理化
体现的数学思想:化归思想
具体方法:平方法
检验
解有理方程
去根号
开始
是
观察分析的方法也是解无理方程的一种好方法
不是
舍去
写出原方程的根
②检验是否符合实际意义
①检验是否是所列方程的解
解方程
列方程
找等量
关系
设元
审题
PAGE
18
1.总结代数方程的分类情况;
2.总结本章知识点之间的内在联系
化归思想
高次化低次;降次的方法:因式分解,换元
分式化整式;化整式的方法:去分母,换元
无理化有理;化有理方程的方法:平方法,换元
多元化一元。代入和加减消元
一、整式方程的解法
1.一元一次方程和一元二次方程的解法
一元一次方程的解法同学们都很熟练了,我们主要回顾一下一元二次方程的解法。
例题 用适当的方法解下列方程:
(1)(2x+1)2=25 (2) (3)3x2+8x-1=0 (4) x2-9x=0
解:(1)两边直接开平方,得 2x+1=±5
∴2x+1=5或2x+1=-5
即 x=2或x=-3
∴原方程的解为x1=2,x2=-3
(2)在方程两边同除以2,得
移项,得
方程配方,得
即
利用直接开平方法,得
∴原方程的解为,
(3),
∴原方程有实数解。
∴,
(4)方程左边因式分解,得 x(x-9)=0
∴x1=0,x2=9
一元二次方程的解法主要有四种:
(1)直接开平方法:
适用于(mx+n)2=h (h≥0)的一元二次方程。
(2)配方法:
适用于所有化为一般形式后的一元二次方程。但是,具有二次项系数为1,一次项系数为偶数特点的一元二次方程,用配方法解才较简便。
配方法是通过配方将一元二次方程化成(mx+n)2=h (h≥0)的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法。
其基本步骤是:
①首先在方程两边同除以二次项系数,把二次项系数化为1;
②把常数项移到等式的右边;
③方程两边同时加上一次项系数一半的平方;
④方程左边写成完全平方式,右边化简为常数;
⑤利用直接开平方法解此方程
用配方法解一元二次方程要注意,当二次项系数不为1时,一定要化为1,然后才能方程两边同时加上一次项系数一半的平方
(3)公式法:
适用于解一般形式的一元二次方程。利用公式可以解所有的一元二次方程。
注意:当b2-4ac≥0时,方程才有实数解;当b2-4ac<0时,原方程无实数解。
(4)因式分解法:
适用于方程右边是0,左边是易于分解成两个一次因式乘积的一元二次方程。
2.含字母系数的整式方程的解法
例题 解下列关于x的方程
(1)(3a-2)x=2(3-x)
(2)bx2-1=1-x2(b≠-1)
解(1)去括号,得 3ax-2x=6-2x
移项,得 3ax-2x+2x=6
合并同类项,得 3ax=6 ※
当a≠0时,方程※是一元一次方程,解得 ;
当a=0时,方程※变成 0·x=6,这时不论x取什么值,等式0·x=6都不成立,因此方程无解。
所以,当a≠0时,原方程的根是;当a=0时,原方程无解。
(2)移项,得 bx2+x2=1+1
合并同类项,得(b+1)x2=2
因为b≠-1,所以b+1≠0
两边同除以b+1,得 ※
当b+1>0时,由方程※解得 ;
当b+1<0时,方程※中,这时方程没有实数根。
所以,当b+1>0时,原方程的根是,;
当b+1<0时,原方程没有实数根。
3.特殊的高次方程的解法
(1)二项方程的解法
二项方程的定义:
如果一元n次方程的一边只有含未知数的一项和非零的常数项,另外一边是零,那么这样的方程叫做二项方程。
关于x的一元n次二项方程的一般形式是
二项方程的解法及根的情况:
一般地,二项方程可变形为
可见,解一元n次二项方程,可以转化为求一个已知数的n次方根,运用开方运算可以求出这个方程的根。
二项方程的根的情况:
对于二项方程,
当n为奇数时,方程只有且只有一个实数根。
当n为偶数时,如果,那么方程有两个实数根,且这两个实数根互为相反数;如果,那么方程没有实数根。
例题 判断下列方程是不是二项方程,如果是二项方程,求出它的根。
(1)x3-64=0 (2)x4+x=0
(3)x5= -9 (4)x3+x=1
解:(1)、(3)是二项方程,(2)、(4)不是二项方程。
下面解方程(1)、(3):
(1)移项,得 x3=64
开方,得
即 x=4
(3)开方,得
即
(2)双二次方程的解法
双二次方程的定义:
只含有偶数次项的一元四次方程,叫做双二次方程。
关于x的双二次方程的一般形式是
双二次方程的解法:
可以用“换元法”解形如的双二次方程。就是用y代替方程中的x2,同时用y2代替x4,将方程转化为关于y的一元二次方程
ay2+by+c=0
解这个关于y的一元二次方程即可。
通过换元,把双二次方程转化为一元方程体现了“降次”的策略。
例题 判断下列方程是不是双二次方程,如果是,求出它的根:
(1)x4-9x2+14=0 (2)x4+10x+25=0
(3)2x4-7x3-4=0 (4)x4+9x2+20=0
解:(1)、(4)是双二次方程,(2)、(3)不是双二次方程。
下面解方程(1)、(4):
(1) 设x2=y,则x4=y2,于是原方程可化为
y2-9y+14=0
解这个关于y的方程,得
y1=2,y2=7
由y1=2,得x2=2,解得
由y2=7,得x2=7,解得
所以,原方程的根是
x1=,x2=,x3=,x4=
(4)设x2=y,则x4=y2,于是原方程可化为
y2+9y+20=0
解这个关于y的方程,得
y1=-4,y2=-5
由y1=-4,得x2=-4,它没有实数根;
由y2=-5,得x2=-5,它也没有实数根
所以,原方程没有实数根。
(3)因式分解法解高次方程
解高于一次的方程,基本思想就是是“降次”,对有些高次方程,可以用因式分解的方法降次。
用因式分解的方法时要注意:一定要使方程的一边为零,另一边可以因式分解。
例题 解下列方程:
(1)2x3+7x2-4x=0 (2)x3-2x2+x-2=0
解:(1)方程左边因式分解,得
x(2x2+7x-4)=0
x(x+4)(2x-1)=0
得x=0或x+4=0或2x-1=0
∴原方程的根是 x=0,x=-4,x=
注意:不要漏掉x=0这个根!
(2)方程左边因式分解,得
(x3-2x2) +(x-2)=0
x2(x-2)+(x-2)=0
(x-2)(x2+1)=0
即 x-2=0或x2+1=0
解方程x-2=0得 x=2
方程x2+1=0没有实数根
所以,原方程的根是 x=2
1. 字母系数方程的讨论
关于ax=b的解有三种情况
关于a=m的解的情况
解方程(1)
(2)
2、特殊高次方程的解法
一般地,二项方程可转化为,转化为求一个数的n次方根,解关于x的双二次方程换元法,y代替,转化为关于y的一元二次方程方程可转化为等号左边是多项式,右边是零。用因式分解的方法可得A·B=0从而转化成 A = 0或 B = 0
3、分式方程的解法
解分式方程的基本思路是:
去分母的关键是确定最简公分母,
在转化过程中要注意不要漏乘,不忘检验。
二、可化为一元二次方程的分式方程的解法
1.适宜用“去分母”的方法的分式方程
解分式方程,通常是通过方程两边同乘以方程中各分式的最简公分母,约去分母,化为整式方程来解。
解分式方程要注意验根!
例题 解下列方程
分析:本例是一道分式方程,通常采用去分母法。
(1)首先应观察各项分母,如能分解因式必须先分解因式,如本例x2-17x+60可分解因式为(x-5)(x-12).
(2)分解因式后再找各分母的最小公倍式.如本例为“(x-5)(x-12)”.
(3)用此整式去乘方程的每一项,便可约去分母,将分式方程转化为整式方程求解.
(4)最后应检验,至此例可找到本例完整解答.
解:原方程就是
,
方程两边都乘以,约去分母,得
,
整理后,得
.
解这个方程,得
.
检验:,
∴ 均为原方程根.
在去分母的过程中要注意两点:(1)必须注意符号的变化规律(如本例“12-x”与“x-12”的关系);(2)用整式乘以方程的每一项,一项都不能漏.
2.适宜用“换元法”的分式方程
适宜用换元法的分式方程有两种,一是二次项与一次项相同的,采取同底换元法;二是不看系数,方程的未知项呈倒数关系的,可采取倒数换元法,
下面的例题中的两个方程,分别具有这两种特点。
例题 解下列方程:
(1);
(2).
(1)分析:观察方程(1)可发现二次项底数与一次项未知底数相同,因而,可考虑同底换元法为宜.
解:(1)设.则原方程可化为
,
,
∴ .
当y1=-2时,即;
当y2=-3时,即.
∴ 均为原方程的根.
(2)分析:观察方程(2)可发现这个方程左边两个分式中的与互为倒数,根据这个特点,可以用倒数换元法来解.
解:设,那么,于是原方程变形为
,
去分母,得 ,
,
解得 y1=,y2=1.
当 y=时,.
去分母并整理,得
.
解得 .
当y=1时,即.
去分母并整理,得
.
检验:把分别代入原方程的分母,各分母都不等于0,所以它们都是原方程的根.
∴原方程根是:.
由此可以看出,解分式方程“转化”为整式方程(一元一次方程或一元二次方程)用去分母法是基础方法,解分式方程应首先考虑用基本方法求解,然后再根据分式方程特点,考虑换元法,便可达到转化的目的,找到思路.对于解题过程的每一个步骤都不能疏忽,才能正确求解.
4、用换元法解分式方程
1.原方程可看作某一分式的二次方程.
2.原方程含有未知数的几个分式有互为倒数的关系.
特别注意:换元法解分式方程需要验根两次
第1次检验y的方程是否有增根
第2次是回代后的关于x两个方程是否有增根
例题
解方程 时,设 y =________,
则原方程化为关于y 的整式方程是:____________________。
解方程:(4x+1)(3x+1)(2x+1)(x+1)=3
设:5x+1=a,
∴原方程的根是
5、无理方程的解法
代数式可分为有理式和无理式,有理式又可分为整式和分式。通过比较,我们可以看到代数式和实数分类结构相同,如下图所示∶
,
我们继续定义∶有理方程和无理方程统称代数方程。代数方程结构如下∶
无理方程的定义∶可写为含有未知数的方程叫做无理方程。
解无理方程的基本思路是把无理方程化为有理方程,通常采用“两边平方”的方法解。对有些特殊的无理方程,可以用“换元法”解。
解无理方程一定要验根!
在初中阶段,我们主要学习下面两种无理方程的解法。
1.只有一个含未知数根式的无理方程
当方程中只有一个含未知数的二次根式时,可先把方程变形,使这个二次根式单独在一边;然后方程的两边同时平方,将这个方程化为有理方程。
例题 解下列方程:
(1) (2)
解:(1)两边平方,得 4(x-3)=(x-6)2
整理,得 x2-16x+48=0
解这个方程,得 x1=4,x2=12
经检验,x=4是增根,舍去;x=12是原方程的根。
所以,原方程的根是 x=12
(2)原方程可变形为
两边平方,得 (3-x)2=2x-3
整理,得 x2-8x+12=0
解得 x1=2,x2=6
经检验,x=2是原方程的根;x=6是增根,舍去。
所以,原方程的根是x=2
2.有两个含未知数根式的无理方程
当方程中有两个含未知数的二次根式时,可先把方程变形,使乙个二次根式单独在一边,另外一个二次根式在方程的另一边;然后方程的两边同时平方,将这个方程化为有理方程。
例题 解下列方程:
(1) (2)
解:(1)原方程可变形为
两边平方,得 x2-2=2x+1
整理,得 x2-2x-3=0
解得 x1=-1,x2=3
经检验,x=-1是增根,舍去;x=3是原方程的根。
所以,原方程的根是 x=3
3.适宜用换元法解的无理方程
如果无理方程中,二次根式里面的未知项和二次根式外面的未知项相同,可以使用换元法来解。
例题 解方程
解:设=y,则3x2-6x+12=3y2 ,则3x2-6x=3y2-12
原方程化为 2y=3y2-12+4
整理,得 3y2-2y-8=0
解得 y1=2,y2=
当y=2时,=2,=4,解得x=0或x=2;
y=时,=,次方程无解。
经检验,x=0,x=2都是原方程的根。
所以,原方程的根是 x1=0,x2=2
解无理方程的一般步骤:
6、有关增根的问题
增根产生的原因:
在解分式方程或无理方程时,将方程转化成整式方程或
有理方程时,扩大了未知数的取值范围,从而产生了增根
如何检验是否增根
将解分式方程转化成整式方程的根代入最简公分母,若使最简公分母为零的根为原方程的增根,否则为原方程的根将解无理方程转化成有理方程的根代入原方程的左右两边,若使方程左右两边的值不相等的根为增根,否则为方程的根。
练习∶解无理方程∶
7、二元二次方程(组)
一、由一个二元一次方程和一个二元二次方程组成的方程组
代入消元法、因式分解降次法和利用根与系数关系
【例1】解方程组
分析:由于方程(1)是二元一次方程,故可由方程(1),得,代入方程(2)消去.
解:由(1)得: (3)
将(3)代入(2)得:,解得:
把代入(3)得:;把代入(3)得:.
∴原方程组的解是:.
说明:(1) 解由一个二元一次方程和一个二元二次方程组成的方程组的步骤:
①由二元一次方程变形为用表示的方程,或用表示的方程(3);
②把方程(3)代入二元二次方程,得一个一元二次方程;
③解消元后得到的一元二次方程;
④把一元二次方程的根,代入变形后的二元一次方程(3),求相应的未知数的 值;
⑤写出答案.
(2) 消,还是消,应由二元一次方程的系数来决定.若系数均为整数,那 么最好消去系数绝对值较小的,如方程,可以消去,变形 得,再代入消元.
(3) 消元后,求出一元二次方程的根,应代入二元一次方程求另一未知数的值, 不能代入二元二次方程求另一未知数的值,因为这样可能产生增根,这一点 切记.
【例2】解方程组
分析:本题可以用代入消元法解方程组,但注意到方程组的特点,可以把、看成是方程的两根,则更容易求解.
解:根据一元二次方程的根与系数的关系,把、看成是方程的两根,解方程得:.
∴ 原方程组的解是:.
说明:(1) 对于这种对称性的方程组,利用一元二次方程的根与系数的关系构造方程时,未知数要换成异于、的字母,如.
(2) 对称形方程组的解也应是对称的,即有解,则必有解.
课堂练习
二、由两个二元二次方程组成的方程组
1.可因式分解型的方程组
方程组中的一个方程可以因式分解化为两个二元一次方程,则原方程组可转化为两个方程组,其中每个方程组都是由一个二元二次方程和一个二元一次方程组成.
【例3】解方程组
分析:注意到方程,可分解成,即得或,则可得到两个二元二次方程组,且每个方程组中均有一个方程为二元一次方程.
解:由(1)得:
∴ 或
∴ 原方程组可化为两个方程组:
用代入法解这两个方程组,得原方程组的解是:
说明:由两个二元二次方程组成的方程组中,有一个方程可以通过因式分解,化为两个二元一次方程,则原方程组转化为解两个方程组,其中每一个方程组均有一个方程是二元一次方程.
【例4】解方程组
分析:本题的特点是方程组中的两个方程均缺一次项,我们可以消去常数项,可得到一个二次三项式的方程.对其因式分解,就可以转化为例3的类型.
解:(1) –(2)得:
即
∴
∴ 原方程组可化为两个二元一次方程组:.
用代入法解这两个方程组,得原方程组的解是:.
说明:若方程组的两个方程均缺一次项,则消去常数项,得到一个二元二次方程.此方程与原方程组中的任一个方程联立,得到一个可因式分解型的二元二次方程组.
【例5】解方程组
分析:(1) +(2)得:,(1) -(2)得:,分别分解(3)、(4)可得四个二元一次方程组.
解:(1) +(2)得:, (1) -(2)得:.
解此四个方程组,得原方程组的解是:
.
说明:对称型方程组,如、都可以通过变形转化为的形式,通过构造一元二次方程求解.
因式分解法
8、列方程(组)解应用题
1.解下列方程组:
(1) (2)
(3) (4)
2.解下列方程组:
(1) (2)
3.解下列方程组:
(1) (2)
(3) (4)
4.解下列方程组:
(1) (2)
1.在方程中,若设,则原方程化为关于y的方程
是 .
2.当m= 时,关于x的分式方程没有实数解.
3.若关于x的方程有实数根,则a的取值范围是 .
4.用换元法解方程时,可设 =y,这时原方程变为 .
5.方程的根是 ;的根是 ;的根
是 .
6.无理方程的根为,则a的值为 .
7.若a,b都是正实数,且,则 .
8.若a+b=1,且a∶b=2∶5,则2a-b= .
9.当a= 时,方程无实数根.
10.若,则 .
11.下列方程中既不是分式方程,也不是无理方程的有( )
A. B. C.
D. E. F.
12.方程的最简公分母是( )
A.24(x+3)(x-3) B.(x+3)(x-3)2 C.24(x+3)(x-3)2 D.12(x+3)(x-3)2
13.观察下列方程,经分析判断得知有实数根的是( )
A. B. C. D.
14.如果,那么的值是( )
A.1 B.-1 C.±1 D.4
15.方程的解是( )
A.0 B.2 C.0或2 D.
16.设y=x2+x+1,则方程可变形为( )
A.y2-y-2=0 B.y2+y+2=0 C.y2+y-2=0 D.y2-y+2=0
17.若,则a的取值范围是( )
A.全体实数 B.a≥0 C.a≥ D.A≤
18.已知,则相等关系成立的式子是( )
A. B. C. D.
19.关于x的方程的根是( )
A.x=a B.x=-a C.x1=a;x2=- D.x1=a;x2=
20.一个数和它的算术平方根的4倍相等,那么这个数是( )
A.0 B.16 C.0或16 D.4或16
21.; 22.;
23.; 24.;
25.; 26.
用方程解应用题
1、块面积相同的小麦试验田,第一块使用原品种,第二块使用新品种,分别收获小麦9000Kg和15000Kg,已知第一块试验田的每公顷的产量比第二块少3000Kg,分别求这块试验田每公顷的产量。
2、从甲地到乙地有两条公路:一条是全长600Km的普通公路,另一条是全长480Km的告诉公路。某客车在高速公路上行驶的平均速度比在普通公路上快45Km,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需要的时间。
3、从甲地到乙地的路程是15千米,A骑自行车从甲地到乙地先走,40分钟后,B骑自行车从甲地出发,结果同时到达。已知B的速度是A的速度的3倍,求两车的速度。
4、一台甲型拖拉机4天耕完一块地的一半,加一天乙型拖拉机,两台合耕,1天耕完这块地的另一半。乙型拖拉机单独耕这块地需要几天?
5、A做90个零件所需要的时间和B做120个零件所用的时间相同,又知每小时A、B两人共做35个机器零件。求A、B每小时各做多少个零件。
6、某工厂去年赢利25万元,按计划这笔赢利额应是去、今两年赢利总额的20%,今年的赢利额应是多少?
7、某农场原有水田400公顷,旱田150公顷,为了提高单位面积产量,准备把部分旱田改为水田,改完之后,要求旱田占水田的10%,问应把多少公顷旱田改为水田。
8、轮船顺水航行80千米所需要的时间和逆水航行60千米所用的时间相同。已知水流的速度是3千米/时,求轮船在静水中的速度。
二元二次方程组
二次方程
高次方程
一次方程
二元一次方程组
多元方程组
一元方程
分式方程
列方程(组)解应用题
无理方程
有理方程
整式方程
代数方程
使最简公分母不为零
写出方程的根
舍去
检验
整式方程
同乘以最简公分母
分式方程
解分式方程的一般步骤:
通过“去分母”将分式方程转化为整式方程
使最简公分母为零
增长率问题,工程问题,行程问题……
检验
结束
无理方程有理化
体现的数学思想:化归思想
具体方法:平方法
检验
解有理方程
去根号
开始
是
观察分析的方法也是解无理方程的一种好方法
不是
舍去
写出原方程的根
②检验是否符合实际意义
①检验是否是所列方程的解
解方程
列方程
找等量
关系
设元
审题
PAGE
18
