《抽样调查与估计》测试题
图片预览
文档简介
抽样调查与估计
一、选择题
1.下列调查方式,合适的是( )
A.要了解一批灯泡的使用寿命,采用普查方式
B.要了解淮安电视台“有事报道”栏目的收视率,采用普查方式
C.要保证“神舟六号”载人飞船成功发射,对重要零部件的检查采用抽样调查方式
D.要了解外地游客对“淮扬菜美食文化节”的满意度,采用抽样调查方式
2.为了了解一批电视机的寿命,从中抽取了100台电视机进行测试,这个问题的样本是( )
A.这批电视机的寿命 B.抽取的100台电视机 C.100 D.抽取的100台电视机的寿命
3.某班主任老师想了解本班学生平均每月有多少零用钱,随机抽取了10名同学进行调查,他们每月的零用钱数目是(单位:元)10,20,20,30,20,30,10,10,50,100,则该班学生每月平均零用钱约为( )
A. 10元 B. 20元 C. 30元 D. 40元
4.武汉市某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.下面是将某年级60篇学生调
查报告的成绩进行整理,分成5组画出的频数分布直方图.已知从左至右4个小组的频率分别是0.05、0.15、0.35、0.30,那么在这次
评比中被评为优秀的调查报告有(分数大于或等于80分为优秀,且分数为整数)( )(A)18篇(B)24篇 (C)25篇(D)27篇
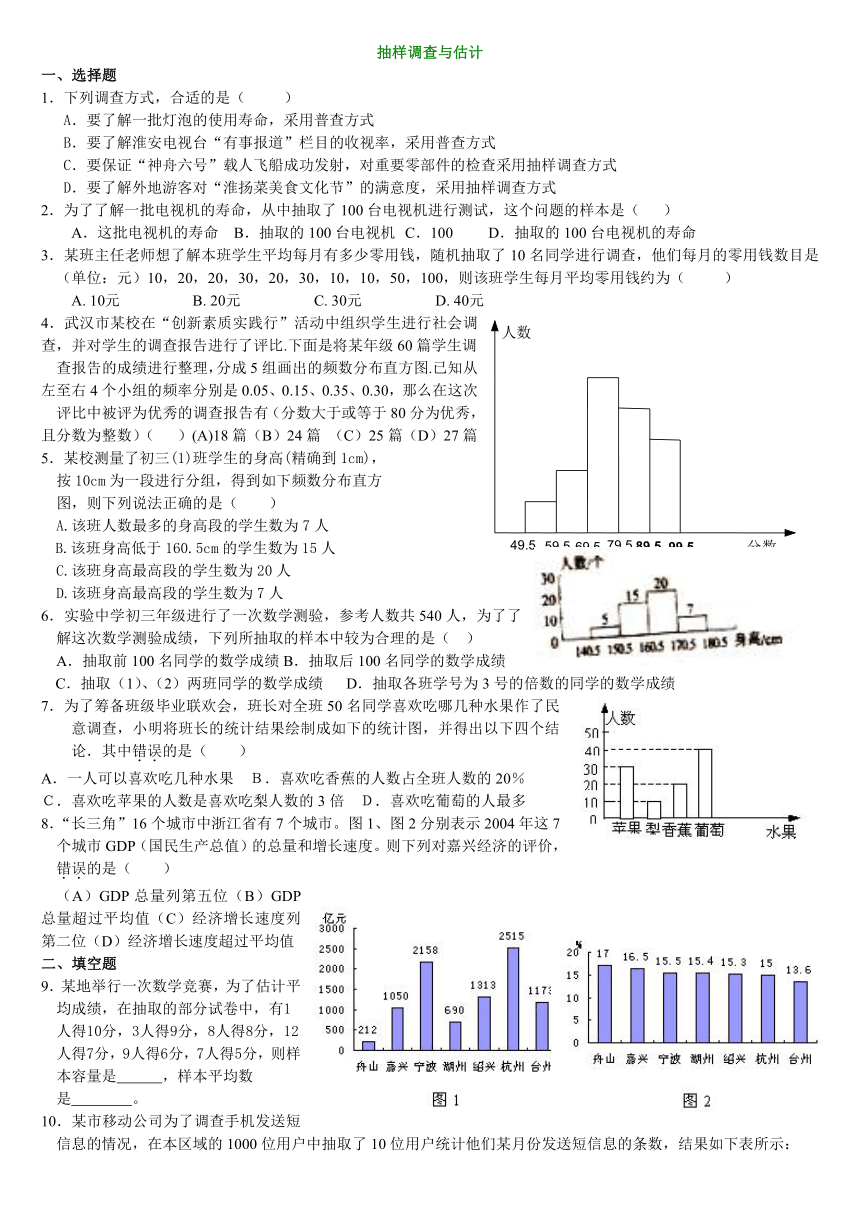
5.某校测量了初三(1)班学生的身高(精确到1cm),
按10cm为一段进行分组,得到如下频数分布直方
图,则下列说法正确的是( )
A.该班人数最多的身高段的学生数为7人
B.该班身高低于160.5cm的学生数为15人
C.该班身高最高段的学生数为20人
D.该班身高最高段的学生数为7人
6.实验中学初三年级进行了一次数学测验,参考人数共540人,为了了解这次数学测验成绩,下列所抽取的样本中较为合理的是( )
A.抽取前100名同学的数学成绩B.抽取后100名同学的数学成绩
C.抽取(1)、(2)两班同学的数学成绩 D.抽取各班学号为3号的倍数的同学的数学成绩
7.为了筹备班级毕业联欢会,班长对全班50名同学喜欢吃哪几种水果作了民意调查,小明将班长的统计结果绘制成如下的统计图,并得出以下四个结论.其中错误的是( )
A.一人可以喜欢吃几种水果 B.喜欢吃香蕉的人数占全班人数的20%
C.喜欢吃苹果的人数是喜欢吃梨人数的3倍 D.喜欢吃葡萄的人最多
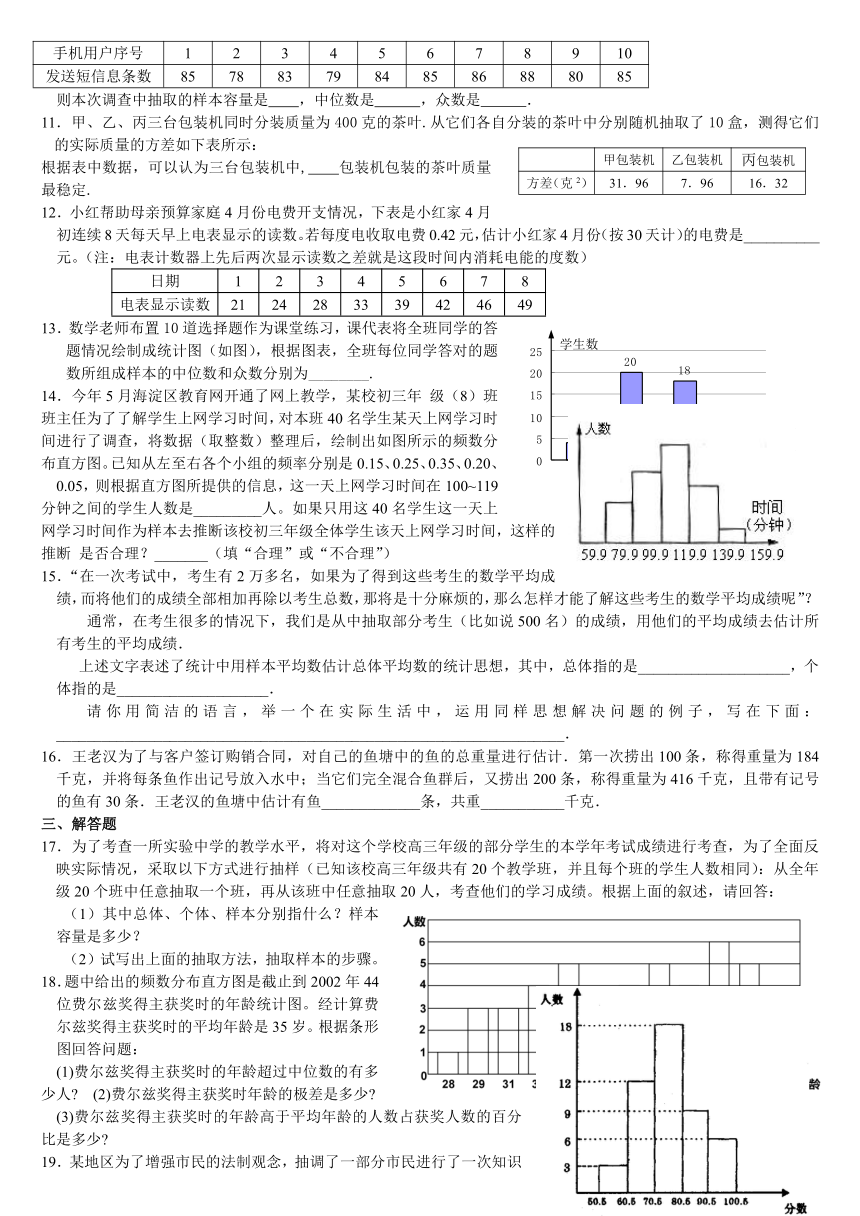
8.“长三角”16个城市中浙江省有7个城市。图1、图2分别表示2004年这7个城市GDP(国民生产总值)的总量和增长速度。则下列对嘉兴经济的评价,错误的是( )
(A)GDP总量列第五位(B)GDP总量超过平均值(C)经济增长速度列第二位(D)经济增长速度超过平均值
二、填空题
9.某地举行一次数学竞赛,为了估计平均成绩,在抽取的部分试卷中,有1人得10分,3人得9分,8人得8分,12人得7分,9人得6分,7人得5分,则样本容量是 ,样本平均数是 。
10.某市移动公司为了调查手机发送短信息的情况,在本区域的1000位用户中抽取了10位用户统计他们某月份发送短信息的条数,结果如下表所示:
手机用户序号 1 2 3 4 5 6 7 8 9 10
发送短信息条数 85 78 83 79 84 85 86 88 80 85
则本次调查中抽取的样本容量是 ,中位数是 ,众数是 .
11.甲、乙、丙三台包装机同时分装质量为400克的茶叶.从它们各自分装的茶叶中分别随机抽取了10盒,测得它们的实际质量的方差如下表所示:
根据表中数据,可以认为三台包装机中, 包装机包装的茶叶质量最稳定.
12.小红帮助母亲预算家庭4月份电费开支情况,下表是小红家4月初连续8天每天早上电表显示的读数。若每度电收取电费0.42元,估计小红家4月份(按30天计)的电费是__________元。(注:电表计数器上先后两次显示读数之差就是这段时间内消耗电能的度数)
日期 1 2 3 4 5 6 7 8
电表显示读数 21 24 28 33 39 42 46 49
13.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成统计图(如图),根据图表,全班每位同学答对的题数所组成样本的中位数和众数分别为________.
14.今年5月海淀区教育网开通了网上教学,某校初三年 级(8)班班主任为了了解学生上网学习时间,对本班40名学生某天上网学习时间进行了调查,将数据(取整数)整理后,绘制出如图所示的频数分布直方图。已知从左至右各个小组的频率分别是0.15、0.25、0.35、0.20、
0.05,则根据直方图所提供的信息,这一天上网学习时间在100~119分钟之间的学生人数是_________人。如果只用这40名学生这一天上网学习时间作为样本去推断该校初三年级全体学生该天上网学习时间,这样的推断 是否合理?_______(填“合理”或“不合理”)
15.“在一次考试中,考生有2万多名,如果为了得到这些考生的数学平均成绩,而将他们的成绩全部相加再除以考生总数,那将是十分麻烦的,那么怎样才能了解这些考生的数学平均成绩呢”?
通常,在考生很多的情况下,我们是从中抽取部分考生(比如说500名)的成绩,用他们的平均成绩去估计所有考生的平均成绩.
上述文字表述了统计中用样本平均数估计总体平均数的统计思想,其中,总体指的是____________________,个体指的是____________________.
请你用简洁的语言,举一个在实际生活中,运用同样思想解决问题的例子,写在下面:___________________________________________________________________.
16.王老汉为了与客户签订购销合同,对自己的鱼塘中的鱼的总重量进行估计.第一次捞出100条,称得重量为184千克,并将每条鱼作出记号放入水中;当它们完全混合鱼群后,又捞出200条,称得重量为416千克,且带有记号的鱼有30条.王老汉的鱼塘中估计有鱼_____________条,共重___________千克.
三、解答题
17.为了考查一所实验中学的教学水平,将对这个学校高三年级的部分学生的本学年考试成绩进行考查,为了全面反映实际情况,采取以下方式进行抽样(已知该校高三年级共有20个教学班,并且每个班的学生人数相同):从全年级20个班中任意抽取一个班,再从该班中任意抽取20人,考查他们的学习成绩。根据上面的叙述,请回答:
(1)其中总体、个体、样本分别指什么?样本容量是多少?
(2)试写出上面的抽取方法,抽取样本的步骤。
18.题中给出的频数分布直方图是截止到2002年44位费尔兹奖得主获奖时的年龄统计图。经计算费尔兹奖得主获奖时的平均年龄是35岁。根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人 (2)费尔兹奖得主获奖时年龄的极差是多少
(3)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖人数的百分比是多少
19.某地区为了增强市民的法制观念,抽调了一部分市民进行了一次知识竞赛,竟赛成绩(得分取整数)进行整理后分成五组,并绘制成频率分布
直方图,请结合(图10)提供的信息,解答下列问题:
(1)抽取了多少人参加竟赛?(2)60.5~70.5这一分数段的频数、频率分别是多少?(3)这次竞赛成绩的中位数落在哪个分数段内?
(4)根据统计图,请你提出一个问题,并回答你所提出的问题.
20.在“3.15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查. 如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为1分、2分、3分、4分.
(1)请问:甲商场的用户满意度分数的众数为 ;
乙商场的用户满意度分数的众数为 .
(2)分别求出甲、乙两商场的用户满意度分数的平均值(计算结果精确到0.01).
(3)请你根据所学的统计知识,判断哪家商场的用户满意度较高,并简要说明理由.
21.某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类.在“深圳读书月”活动期间,为了解图书的借阅情况,图书管理员对本月各类图书的借阅量进行了统计,图1和图2是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
频率分布表
图书种类 频数 频率
自然科学 400 0.20
文学艺术 1000 0.50
社会百科 500 0.25
数学
(1)填充图1频率分布表中的空格.
(2)在图2中,将表示“自然科学”的部分补充完整.
(3)若该学校打算采购一万册图书,请你估算“数学”类图书应采购多少册较合适?
(4)根据图表提供的信息,请你提出一条合理化的建议.
22.某校320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级。为了了解电脑培训的效果,随机抽取32名学生两次考试考分等级的统计图(如图8)。试回答下列问题:⑴这32名学生经过培训,考分等级“不合格”的百分比由_________下降到__________;⑵估计该校320名学生,培训后考分等级为“合格”与优秀的学生共___________名;⑶你认为上述估计合理吗?理由是什么?答:___________,理由:_____________________.
23.初中生的视力状况受到全社会的广泛关注,某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,下图是利用所得数据绘制的频数分布直方图,根据图中提供的信息回答下列问题:
(1)本次调查共抽测了解多少名学生; (2)在这个问题中的样本指什么;
(3)如果视力在4.9∽5.1(含4.9、5.1)均属正常,那 么全市有多少初中生的视力正常?
24.学习了数据的有关知识后,小敏和小红两位同学利用周日在某一路口进行了一次调查,以了解在不同时段内各种机动车辆在此路口的过往情况。调查数据如下表:
车辆时间 摩托车 轿车 面的 中巴车
9:00—9:05 15 22 24 12
11:40—11:45 40 36 32 16
小敏设计了如下图所示的统计图:
小红同学设计了如下图所示的统计图:
你认为那幅统计图能较好的反映不同时间段内各种机动车辆在此路上的过往情况?请说明理由。
抽样调查与估计参考答案
一、1---4:DDCD 5---8:DDDB 二、9.40,7 10.10、84.5、85 11.乙 12.50.4 13.8,9
14.14,不合理 15.所有考生的数学成绩的全体;每一名考生的数学成绩;略 16.1000,约2011
三、17.(1)总体指该校高三年级全体学生本学年的考试成绩;个体指高三年级每个学生本学年的考试成绩;样本是所抽取的20名学生本学年的考试成绩;样本容量是20。(2)抽取的方法是随机抽样法,抽样步骤如下: ①先在这20个班中用抽签法任取一个班;②然后从这个班中按学号用随机数表法或抽签法抽取20名学生,考查其考试成绩。18.(1)因为中位数为岁,所以年龄超过中位数的有22人;
(2)(岁);(3)高于平均年龄的人数为22人,.
19.(1)3+6+9+12+18=48(人)(2)60.5~70.5这一分数段的频数为12,频率为
(3)中位数落在70.5~80.5这一分数段内(4)略
20.(1)3;3(2)甲商场抽查用户数为:500+1000+2000+1000=4500(户) 乙商场抽查用户数为:100+900+2200+1300=4500(户) 所以甲商场满意度分数的平均值= ≈2.78(分)
乙商场满意度分数的平均值= ≈3.04(分) 答:甲、乙两商场用户满意度分数的平均值分别为2.78分、3.04分. (3)因为乙商场用户满意度分数的平均值较高(或较满意和很满意的人数较多),
所以乙商场的用户满意度较高.
21.(1)100,0.05;(2)略;(3)500;(4)略22.(1)75%, 25%; (2)240; (3)合理, 样本选取具有代表性
23.(1)本次调查共抽测了240名学生(2)样本是指240名学生的视力(3)全市有7500名初中生的视力正常
24.小红同学设计的统计图能较好的反映不同时间段内各种机动车辆在此路上的过往情况。因为小敏设计的统计图不仅不容易对两个不同的时间段内各种车辆的过往多少进行比较,而且容易给人造成错误的印象:9:00—9:05这一时间段内轿车、面的、中巴车过往的要比11:40—11:45时间段内过往的多,这是由于两幅图的纵轴单位不同造成的;小红同学将两张统计图合并成了一张,形成了复式统计图,从她的统计图中可以一目了然地看出不同时间段内各种车辆的过往情况。
50
40
30
20
10
0
摩托车 轿车 面的 中巴车
11:40—11:45
9:00—9:05
11:40—11:45
9:00—9:05
摩托车 轿车 面的 中巴车
0
20
40
图书
0
200
400
借阅量/册
图2
图1
摩托车 轿车 面的 中巴车
60
0
30
10
20
1000
600
800
甲商场抽查用户数 乙商场抽查用户数
1300
2200
2000
1000
900
2000
1000
1000
100
500
500
很满意
较满意
不满意
很不满意
8
10
7
9
做对
题数
学生数
甲包装机 乙包装机 丙包装机
方差(克2) 31.96 7.96 16.32
49.5
59.5
69.5
79.5
89.5
99.5
分数
人数
一、选择题
1.下列调查方式,合适的是( )
A.要了解一批灯泡的使用寿命,采用普查方式
B.要了解淮安电视台“有事报道”栏目的收视率,采用普查方式
C.要保证“神舟六号”载人飞船成功发射,对重要零部件的检查采用抽样调查方式
D.要了解外地游客对“淮扬菜美食文化节”的满意度,采用抽样调查方式
2.为了了解一批电视机的寿命,从中抽取了100台电视机进行测试,这个问题的样本是( )
A.这批电视机的寿命 B.抽取的100台电视机 C.100 D.抽取的100台电视机的寿命
3.某班主任老师想了解本班学生平均每月有多少零用钱,随机抽取了10名同学进行调查,他们每月的零用钱数目是(单位:元)10,20,20,30,20,30,10,10,50,100,则该班学生每月平均零用钱约为( )
A. 10元 B. 20元 C. 30元 D. 40元
4.武汉市某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.下面是将某年级60篇学生调
查报告的成绩进行整理,分成5组画出的频数分布直方图.已知从左至右4个小组的频率分别是0.05、0.15、0.35、0.30,那么在这次
评比中被评为优秀的调查报告有(分数大于或等于80分为优秀,且分数为整数)( )(A)18篇(B)24篇 (C)25篇(D)27篇
5.某校测量了初三(1)班学生的身高(精确到1cm),
按10cm为一段进行分组,得到如下频数分布直方
图,则下列说法正确的是( )
A.该班人数最多的身高段的学生数为7人
B.该班身高低于160.5cm的学生数为15人
C.该班身高最高段的学生数为20人
D.该班身高最高段的学生数为7人
6.实验中学初三年级进行了一次数学测验,参考人数共540人,为了了解这次数学测验成绩,下列所抽取的样本中较为合理的是( )
A.抽取前100名同学的数学成绩B.抽取后100名同学的数学成绩
C.抽取(1)、(2)两班同学的数学成绩 D.抽取各班学号为3号的倍数的同学的数学成绩
7.为了筹备班级毕业联欢会,班长对全班50名同学喜欢吃哪几种水果作了民意调查,小明将班长的统计结果绘制成如下的统计图,并得出以下四个结论.其中错误的是( )
A.一人可以喜欢吃几种水果 B.喜欢吃香蕉的人数占全班人数的20%
C.喜欢吃苹果的人数是喜欢吃梨人数的3倍 D.喜欢吃葡萄的人最多
8.“长三角”16个城市中浙江省有7个城市。图1、图2分别表示2004年这7个城市GDP(国民生产总值)的总量和增长速度。则下列对嘉兴经济的评价,错误的是( )
(A)GDP总量列第五位(B)GDP总量超过平均值(C)经济增长速度列第二位(D)经济增长速度超过平均值
二、填空题
9.某地举行一次数学竞赛,为了估计平均成绩,在抽取的部分试卷中,有1人得10分,3人得9分,8人得8分,12人得7分,9人得6分,7人得5分,则样本容量是 ,样本平均数是 。
10.某市移动公司为了调查手机发送短信息的情况,在本区域的1000位用户中抽取了10位用户统计他们某月份发送短信息的条数,结果如下表所示:
手机用户序号 1 2 3 4 5 6 7 8 9 10
发送短信息条数 85 78 83 79 84 85 86 88 80 85
则本次调查中抽取的样本容量是 ,中位数是 ,众数是 .
11.甲、乙、丙三台包装机同时分装质量为400克的茶叶.从它们各自分装的茶叶中分别随机抽取了10盒,测得它们的实际质量的方差如下表所示:
根据表中数据,可以认为三台包装机中, 包装机包装的茶叶质量最稳定.
12.小红帮助母亲预算家庭4月份电费开支情况,下表是小红家4月初连续8天每天早上电表显示的读数。若每度电收取电费0.42元,估计小红家4月份(按30天计)的电费是__________元。(注:电表计数器上先后两次显示读数之差就是这段时间内消耗电能的度数)
日期 1 2 3 4 5 6 7 8
电表显示读数 21 24 28 33 39 42 46 49
13.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成统计图(如图),根据图表,全班每位同学答对的题数所组成样本的中位数和众数分别为________.
14.今年5月海淀区教育网开通了网上教学,某校初三年 级(8)班班主任为了了解学生上网学习时间,对本班40名学生某天上网学习时间进行了调查,将数据(取整数)整理后,绘制出如图所示的频数分布直方图。已知从左至右各个小组的频率分别是0.15、0.25、0.35、0.20、
0.05,则根据直方图所提供的信息,这一天上网学习时间在100~119分钟之间的学生人数是_________人。如果只用这40名学生这一天上网学习时间作为样本去推断该校初三年级全体学生该天上网学习时间,这样的推断 是否合理?_______(填“合理”或“不合理”)
15.“在一次考试中,考生有2万多名,如果为了得到这些考生的数学平均成绩,而将他们的成绩全部相加再除以考生总数,那将是十分麻烦的,那么怎样才能了解这些考生的数学平均成绩呢”?
通常,在考生很多的情况下,我们是从中抽取部分考生(比如说500名)的成绩,用他们的平均成绩去估计所有考生的平均成绩.
上述文字表述了统计中用样本平均数估计总体平均数的统计思想,其中,总体指的是____________________,个体指的是____________________.
请你用简洁的语言,举一个在实际生活中,运用同样思想解决问题的例子,写在下面:___________________________________________________________________.
16.王老汉为了与客户签订购销合同,对自己的鱼塘中的鱼的总重量进行估计.第一次捞出100条,称得重量为184千克,并将每条鱼作出记号放入水中;当它们完全混合鱼群后,又捞出200条,称得重量为416千克,且带有记号的鱼有30条.王老汉的鱼塘中估计有鱼_____________条,共重___________千克.
三、解答题
17.为了考查一所实验中学的教学水平,将对这个学校高三年级的部分学生的本学年考试成绩进行考查,为了全面反映实际情况,采取以下方式进行抽样(已知该校高三年级共有20个教学班,并且每个班的学生人数相同):从全年级20个班中任意抽取一个班,再从该班中任意抽取20人,考查他们的学习成绩。根据上面的叙述,请回答:
(1)其中总体、个体、样本分别指什么?样本容量是多少?
(2)试写出上面的抽取方法,抽取样本的步骤。
18.题中给出的频数分布直方图是截止到2002年44位费尔兹奖得主获奖时的年龄统计图。经计算费尔兹奖得主获奖时的平均年龄是35岁。根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人 (2)费尔兹奖得主获奖时年龄的极差是多少
(3)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖人数的百分比是多少
19.某地区为了增强市民的法制观念,抽调了一部分市民进行了一次知识竞赛,竟赛成绩(得分取整数)进行整理后分成五组,并绘制成频率分布
直方图,请结合(图10)提供的信息,解答下列问题:
(1)抽取了多少人参加竟赛?(2)60.5~70.5这一分数段的频数、频率分别是多少?(3)这次竞赛成绩的中位数落在哪个分数段内?
(4)根据统计图,请你提出一个问题,并回答你所提出的问题.
20.在“3.15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查. 如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为1分、2分、3分、4分.
(1)请问:甲商场的用户满意度分数的众数为 ;
乙商场的用户满意度分数的众数为 .
(2)分别求出甲、乙两商场的用户满意度分数的平均值(计算结果精确到0.01).
(3)请你根据所学的统计知识,判断哪家商场的用户满意度较高,并简要说明理由.
21.某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类.在“深圳读书月”活动期间,为了解图书的借阅情况,图书管理员对本月各类图书的借阅量进行了统计,图1和图2是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
频率分布表
图书种类 频数 频率
自然科学 400 0.20
文学艺术 1000 0.50
社会百科 500 0.25
数学
(1)填充图1频率分布表中的空格.
(2)在图2中,将表示“自然科学”的部分补充完整.
(3)若该学校打算采购一万册图书,请你估算“数学”类图书应采购多少册较合适?
(4)根据图表提供的信息,请你提出一条合理化的建议.
22.某校320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级。为了了解电脑培训的效果,随机抽取32名学生两次考试考分等级的统计图(如图8)。试回答下列问题:⑴这32名学生经过培训,考分等级“不合格”的百分比由_________下降到__________;⑵估计该校320名学生,培训后考分等级为“合格”与优秀的学生共___________名;⑶你认为上述估计合理吗?理由是什么?答:___________,理由:_____________________.
23.初中生的视力状况受到全社会的广泛关注,某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,下图是利用所得数据绘制的频数分布直方图,根据图中提供的信息回答下列问题:
(1)本次调查共抽测了解多少名学生; (2)在这个问题中的样本指什么;
(3)如果视力在4.9∽5.1(含4.9、5.1)均属正常,那 么全市有多少初中生的视力正常?
24.学习了数据的有关知识后,小敏和小红两位同学利用周日在某一路口进行了一次调查,以了解在不同时段内各种机动车辆在此路口的过往情况。调查数据如下表:
车辆时间 摩托车 轿车 面的 中巴车
9:00—9:05 15 22 24 12
11:40—11:45 40 36 32 16
小敏设计了如下图所示的统计图:
小红同学设计了如下图所示的统计图:
你认为那幅统计图能较好的反映不同时间段内各种机动车辆在此路上的过往情况?请说明理由。
抽样调查与估计参考答案
一、1---4:DDCD 5---8:DDDB 二、9.40,7 10.10、84.5、85 11.乙 12.50.4 13.8,9
14.14,不合理 15.所有考生的数学成绩的全体;每一名考生的数学成绩;略 16.1000,约2011
三、17.(1)总体指该校高三年级全体学生本学年的考试成绩;个体指高三年级每个学生本学年的考试成绩;样本是所抽取的20名学生本学年的考试成绩;样本容量是20。(2)抽取的方法是随机抽样法,抽样步骤如下: ①先在这20个班中用抽签法任取一个班;②然后从这个班中按学号用随机数表法或抽签法抽取20名学生,考查其考试成绩。18.(1)因为中位数为岁,所以年龄超过中位数的有22人;
(2)(岁);(3)高于平均年龄的人数为22人,.
19.(1)3+6+9+12+18=48(人)(2)60.5~70.5这一分数段的频数为12,频率为
(3)中位数落在70.5~80.5这一分数段内(4)略
20.(1)3;3(2)甲商场抽查用户数为:500+1000+2000+1000=4500(户) 乙商场抽查用户数为:100+900+2200+1300=4500(户) 所以甲商场满意度分数的平均值= ≈2.78(分)
乙商场满意度分数的平均值= ≈3.04(分) 答:甲、乙两商场用户满意度分数的平均值分别为2.78分、3.04分. (3)因为乙商场用户满意度分数的平均值较高(或较满意和很满意的人数较多),
所以乙商场的用户满意度较高.
21.(1)100,0.05;(2)略;(3)500;(4)略22.(1)75%, 25%; (2)240; (3)合理, 样本选取具有代表性
23.(1)本次调查共抽测了240名学生(2)样本是指240名学生的视力(3)全市有7500名初中生的视力正常
24.小红同学设计的统计图能较好的反映不同时间段内各种机动车辆在此路上的过往情况。因为小敏设计的统计图不仅不容易对两个不同的时间段内各种车辆的过往多少进行比较,而且容易给人造成错误的印象:9:00—9:05这一时间段内轿车、面的、中巴车过往的要比11:40—11:45时间段内过往的多,这是由于两幅图的纵轴单位不同造成的;小红同学将两张统计图合并成了一张,形成了复式统计图,从她的统计图中可以一目了然地看出不同时间段内各种车辆的过往情况。
50
40
30
20
10
0
摩托车 轿车 面的 中巴车
11:40—11:45
9:00—9:05
11:40—11:45
9:00—9:05
摩托车 轿车 面的 中巴车
0
20
40
图书
0
200
400
借阅量/册
图2
图1
摩托车 轿车 面的 中巴车
60
0
30
10
20
1000
600
800
甲商场抽查用户数 乙商场抽查用户数
1300
2200
2000
1000
900
2000
1000
1000
100
500
500
很满意
较满意
不满意
很不满意
8
10
7
9
做对
题数
学生数
甲包装机 乙包装机 丙包装机
方差(克2) 31.96 7.96 16.32
49.5
59.5
69.5
79.5
89.5
99.5
分数
人数
