一次函数专题复习

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
一次函数与不等式
一、学习指引
1.知识要点
（1）图形与平面直角坐标系（2）一次函数与不等式（3）一次函数与不等式的应用
2.方法指引
（1） 熟知一次函数的图象与性质，实际问题一定要注意自变量取值.
（1） 一次函数的图象在X轴上方的部分X的取值相当于一次不等式大于0的解；一次函数的图象在X轴下方的部分X的取值相当于一次不等式小于0的解.
（1） 函数题一定要注意一种重要的数学思想即数形结合.
（1） 会用图象上的点、实际问题中的变量关系以及图象的形状和位置或具有的性质等各种条件，灵活运用转化、分类讨论和方程等思想方法，用待定系数法来确定函数的解析式.
二、典型例题
（一）填空与选择
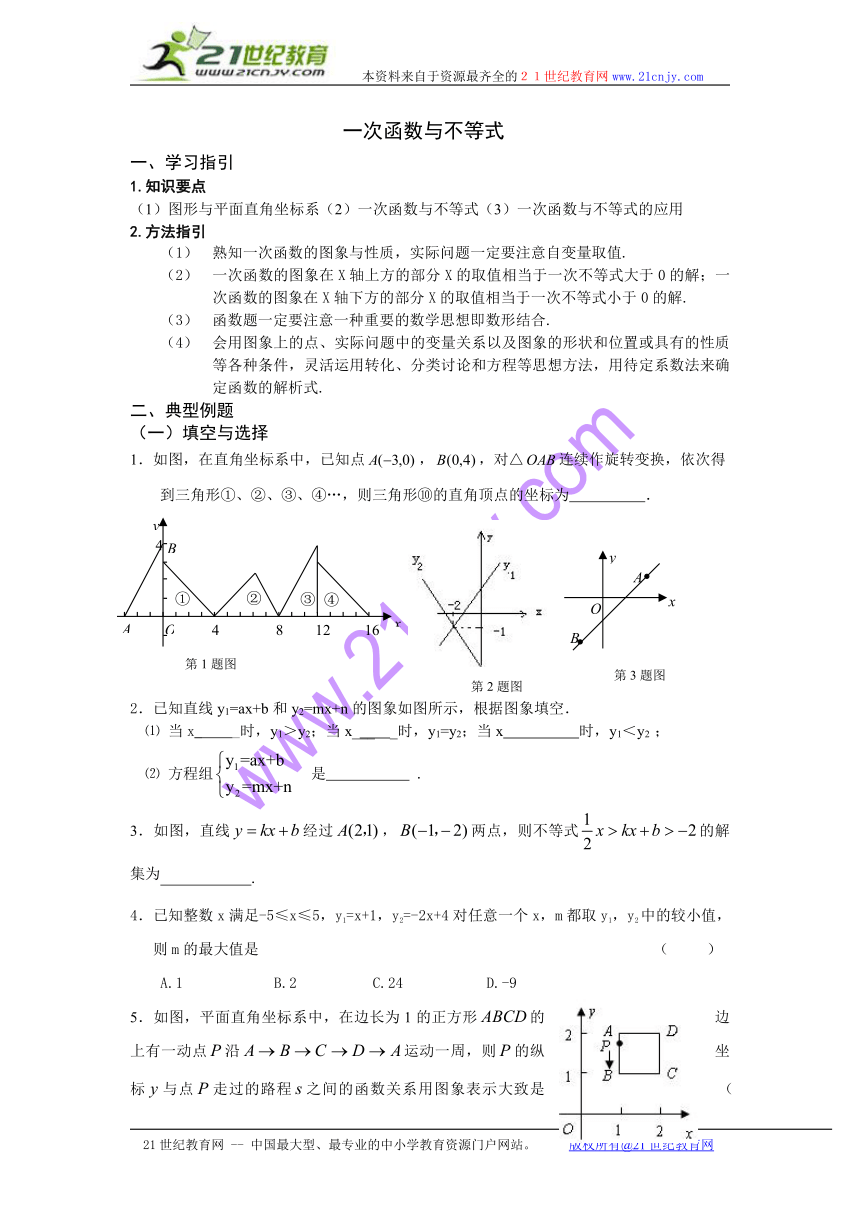
1．如图，在直角坐标系中，已知点，，对△连续作旋转变换，依次得到三角形①、②、③、④…，则三角形⑩的直角顶点的坐标为　　 　．
2．已知直线y1=ax+b和y2=mx+n的图象如图所示，根据图象填空．
⑴ 当x_ _时，y1＞y2；当x___ _时，y1=y2；当x 时，y1＜y2 ；
⑵ 方程组 是 .
3．如图，直线经过，两点，则不等式的解集为 .
4．已知整数x满足-5≤x≤5，y1=x+1，y2=-2x+4对任意一个x，m都取y1，y2中的较小值，则m的最大值是 （ ）
A.1 B.2 C.24 D.-9
5．如图，平面直角坐标系中，在边长为1的正方形的边上有一动点沿运动一周，则的纵坐标与点走过的路程之间的函数关系用图象表示大致是 （ ）
6．正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别
在直线(k＞0)和x轴上，
已知点B1(1，1)，B2(3，2)， 则第n
个正方形的边为________，An的坐标是_____
_________．Bn的坐标是______________．
（二）例题讲解
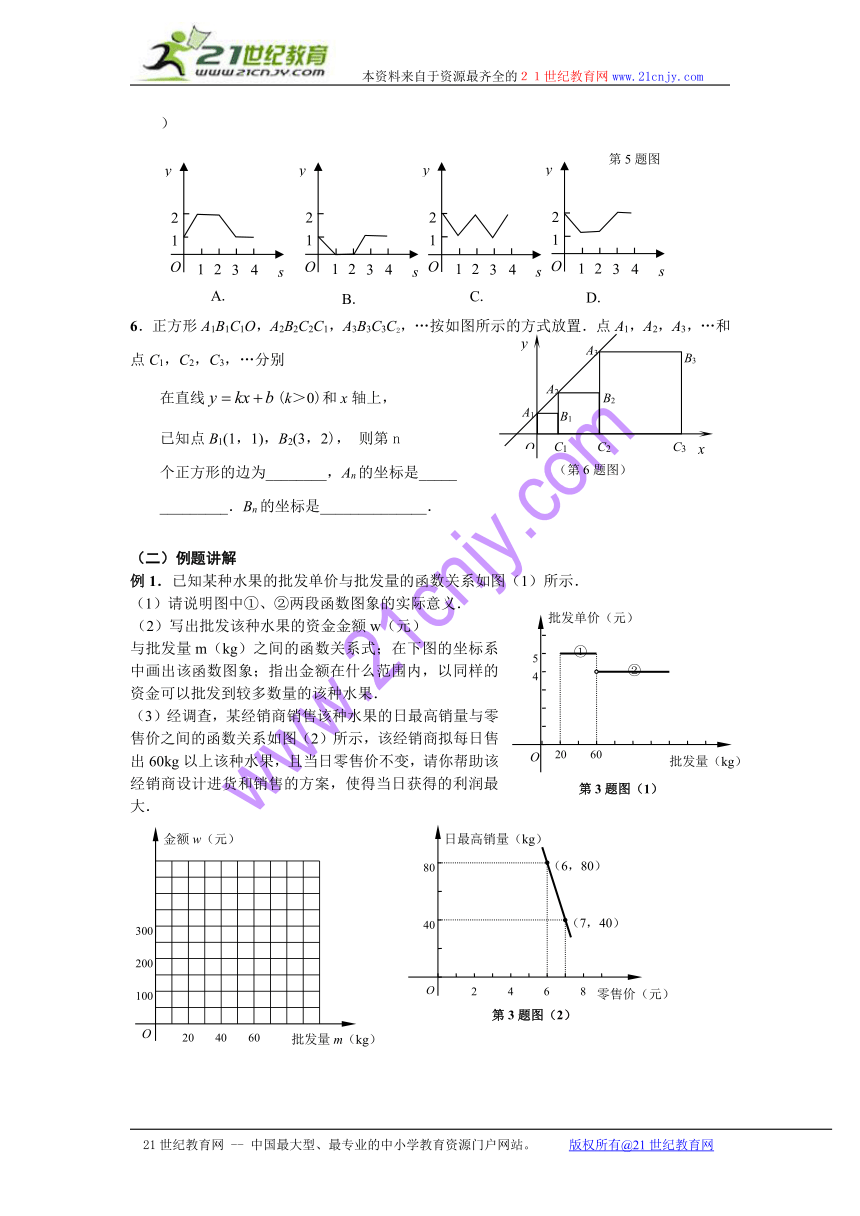
例1．已知某种水果的批发单价与批发量的函数关系如图（1）所示．
（1）请说明图中①、②两段函数图象的实际意义．
（2）写出批发该种水果的资金金额w（元）
与批发量m（kg）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．
（3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商拟每日售出60kg以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．
例2．如图①，一条笔直的公路上有A、B、C 三地，B、C 两地相距 150 千米，甲、乙两辆汽车分别从B、C 两地同时出发，沿公路匀速相向而行，分别驶往C、B 两地．甲、乙两车到A 地的距离、（千米）与行驶时间 x（时）的关系如图②所示．
根据图象进行以下探究：
⑴请在图①中标出 A地的位置，并作简要的文字说明；
⑵求图②中M点的坐标，并解释该点的实际意义．
⑶在图②中补全甲车的函数图象，求甲车到 A地的距离与行驶时间x的函数关系式．
⑷A地设有指挥中心，指挥中心及两车都配有对讲机，两部对讲机在15千米之内（含15千米）时能够互相通话，求两车可以同时与指挥中心用对讲机通话的时间．
（5）两部对讲机之间可以通话的时间为多少？
例3.（2009年江苏省）某加油站五月份营销一种油品的销售利润（万元）与销售量（万升）之间函数关系的图象如图中折线所示，该加油站截止到13日调价时的销售利润为4万元，截止至15日进油时的销售利润为5.5万元．（销售利润＝（售价－成本价）×销售量）请你根据图象及加油站五月份该油品的所有销售记录提供的信息，解答下列问题：
（1）求销售量为多少时，销售利润为4万元；
（2）分别求出线段AB与BC所对应的函数关系式；
（3）我们把销售每升油所获得的利润称为利润率，那么，在OA.AB.BC三段所表示的销售信息中，哪一段的利润率最大？（直接写出答案）
例4．在平面直角坐标系中，边长为2的正OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y＝x上时停止旋转，旋转过程中，边交直线y＝x于点M，BC边交x轴于点N（如图）．
（1）求OA在旋转过程中所扫过的面积；
（2）旋转过程中，当MN和AC平行时，求正方形OABC旋转的度数；
（3）设△MBN的周长为p，在正方形OABC旋转的过程中，p值是否有变化？请证明你的结论
一次函数与不等式同步训练
【基础巩固】
一、选择与填空
1．已知一次函数,函数随着的增大而减小，且其图象不经过第一象限，则的取值范围是（ ）
A、 B、 C、 D
2．已知关于的函数图象如图所示，则当时，自变量的取值范围是（ ）
A． B．或 C． D．或
3．如图，点A、B、C、D在一次函数的图象上，它们的横坐标依次为-1、1、2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积这和是 （ ）
A． B． C． D．
4.如图，点A的坐标为(－1，0)，点B在直线y=x上运动，当线段AB最短时，点B的坐标为 ( ) A.（0，0） B.（，） C.（－，－） D.（－，－）
5.如图，在平面直角坐标系xOy中，，，，，…，以
为对角线作第一个正方形，以为对角线作第二个正方形，以为
对角线作第三个正方形，…，如果所作正方形的对角线都在y轴上，且
的长度依次增加1个单位，顶点都在第一象限内（n≥1，且n为整数）．那么
的纵坐标为___________；用n的代数式表示的纵坐标___________ ．
二、解答题
1．教室里放有一台饮水机（如图），饮水机上有两个放水管．课间同学们依次到饮水机前用茶杯接水．假设接水过程中水不发生泼洒，每个同学所接的水量都是相等的．两个放水管同时打开时，他们的流量相同.放水时先打开一个水管，过一会儿，再打开第二个水管，放水过程中阀门一直开着．饮水机的存水量y（升）与放水时间x（分钟）的函数关系如图所示：
（1）求出饮水机的存水量y（升）与放水时间x（分钟）(x≥2)的函数关系式；
（2）如果打开第一个水管后，2分钟时恰好有4个同学接水结束，则前22个同学接水结束共需要几分钟？
（3）按（2）的放法，求出在课间10分钟内班级中最多有多少个同学能及时接完水？
2．一辆客车从甲地开往甲地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为y1（km），出租车离甲地的距离为y2（km），客车行驶时间为x（h），y1，y2与x的函数关系图象如图12所示：
（1）根据图象，直接写出y1，y2关于x的函数关系式。
（2）分别求出当x=3，x=5，x=8时，两车之间的距离。
（3）若设两车间的距离为S（km），请写出S关于x的函数关系式。
（4）甲、乙两地间有A、B两个加油站，相距200km，若客车进入A站加油时，出租车恰好进入B站加油。求A加油站到甲地的距离。
【能力拓展】
一、选择与填空
1．线段（1≤≤3，），当a的值由-1增加到2时，该线段运动所经过的平面区域的面积为 （ ）
A．6 B．8 C．9 D．10
2.如图，把直线向上平移后得到直线AB，直线AB经过点，且，则直线AB的解析式是（ ）
A． B． C． D．
3．函数 y1=x+1与y2=ax+b的图象如图所示，这两个函数图象如图所示，那么使y1,y2的值都大于零的x的取值范围是
4.已知M(a，b)是平面直角坐标系xOy中的点，其中a是从l，2，3三个数中任取的一个数，b是从l，2，3，4四个数中任取的一个数．定义“点M(a，b)在直线x+y=n上”为事件 (2≤n≤7，n为整数)，则当的概率最大时，n的所有可能的值为______．
5．已知直线，，，若无论取何值，总取、、中的最小值，则的最大值为______．
6．如图所示，已知：点，，在内依次作等边三角形，使一边在轴上，另一个顶点在边上，作出的等边三角形分别是第1个，第2个，第3个，…，则第个等边三角形的边长等于 ．
二、解答题
1．某公司装修需用A型板材240块、B型板材180块，A型板材规格是60 cm×30 cm，B型板材规格是40 cm×30 cm．现只能购得规格是150 cm×30 cm的标准板材．一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（图15是裁法一的裁剪示意图）
裁法一 裁法二 裁法三
A型板材块数 1 2 0
B型板材块数 2 m n
设所购的标准板材全部裁完，其中按裁法一裁x张、按裁法二裁y
张、按裁法三裁z张，且所裁出的A、B两种型号的板材刚好够用．
（1）上表中，m = ，n = ；
（2）分别求出y与x和z与x的函数关系式；
（3）若用Q表示所购标准板材的张数，求Q与x的函数关系式，
并指出当x取何值时Q最小，此时按三种裁法各裁标准板材
多少张？
2．“5 12”汶川大地震后，某健身器材销售公司通过当地“红十字会”向灾区献爱心，捐出了五月份全部销售利润．已知该公司五月份只售出甲、乙、丙三种型号器材若干台，每种型号器材不少于8台，五月份支出包括这批器材进货款64万元和其他各项支出（含人员工资和杂项开支）3.8万元.这三种器材的进价和售价如下表，人员工资y1(万元)和杂项支出y2（万元）分别与总销售量x（台）成一次函数关系(如图).
（1）求y1与x的函数解析式； （2）求五月份该公司的总销售量；
（3）设公司五月份售出甲种型号器材t台，五月份总销售利润为W（万元），求W与t的函数关系式；（销售利润＝销售额－进价－其他各项支出）
（4）请推测该公司这次向灾区捐款金额的最大值.
单位万元/台 甲 乙 丙
进价 0．9 1．2 1．1
售价 1．2 1．6 1．3
例题与同步练习参考答案
一次函数与不等式（典型例题）
（一）填空与选择
１．（36，0）　　2. (1)>-2 =-2 <-2 (2) 3．
4．B 5.D 6．2n-1 ( 2n-1 -1, 2n-1 )
（二）例题答案
例1. （1）
（2）
当（3）当零售价为X时，日最高销量为y千克。则y=-40x+320.
利润z=(x-4)(-40x+320)=-40(x-6)2+160.所以当零售价为6元是，利润最大为160元，此时应进80千克水果。
例2. ⑴A 地位置如图所示．使点A满足AB ∶AC＝2∶3 .
⑵乙车的速度150÷2＝75千米/时,
，∴M(1.2，0)
所以点 M表示乙车 1.2 小时到达 A地。
⑶甲车的函数图象如图所示．
当时，；
当时，.
⑷由题意得，得； ，得.
∴ ∴两车同时与指挥中心通话的时间为小时.
例3(1)4 (2)y=1.5x-2,y=1.1x (3)AB
例4.(1)s=
(2)旋转22.5°
（3）延长BA交Y轴于点P，证明≌△MON,MN=MP,P=4.
一次函数与不等式（同步练习）
【基础巩固】
一、填空与选择
1．D 2.B 3.B 4．D 5.2,(n+1)2/2
二、解答题
1．（1） （2）由图可得每个同学接水量为0.25升,则前22个同学需接水5.5升,存水量12.5升,故,得x=7.
(3)当x=10时,存水量,所以课间10分钟最多有32人及时接完水.
2.解：（1）y1=60x（0≤x≤10） y2=－100x+600（0≤x≤6）
（2）当x=3时，y1=180，y2=300， ∴y2－y1=120
当x=5时，y1=300，y2=100，∴y1－y2=200
当x=8时，y1=480，y2=0 ∴y1－y2=y1=480
（3） 1600x+600 （0≤x≤）
S= 1600x－600 （≤x≤6）
60x （6≤x≤10）
（4）由题意得：S=200
①当0≤x≤时，－160x+600=200，∴x=，∴y1=60x=150km.
②当≤x≤6时，160x－600=200，∴x=5，∴y1=300km.
③当6≤x≤10时，60x≥360，不合题意.
即：A加油站到甲地距离为150km或300km.
【能力拓展】
一、选择题
1.A 2.D 3.-1二、解答题
1. 解：（1）0 ，3．
（2）由题意，得， ∴． ，∴．
（3）由题意，得 ．
整理，得 ． 由题意，得 ( http: / / www. / )
解得 x≤90．
【注：事实上，0≤x≤90 且x是6的整数倍】由一次函数的性质可知，当x=90时，Q最小．此时按三种裁法分别裁90张．75张．0张．
2．解：（1）y1=0.05x+0.2 (2)y1+y2=3.8 的X=60 (3)设乙P台0.9t+1.2p+1.1(60-t-p)=64
P=2t-20 w=0.5t+4.2 (4) 当t=24时w最大为16.2
y
x
O
A
B
y
x
O
A
B
①
②
③
④
4
8
12
16
4
第1题图
第3题图
第2题图
第5题图
1
2
3
4
1
2
y
s
O
1
2
3
4
1
2
y
s
O
s
1
2
3
4
1
2
y
s
O
1
2
3
4
1
2
y
O
A.
B.
C.
D.
y
x
O
C1
B2
A2
C3
B1
A3
B3
A1
C2
（第6题图）
O
60
20
4
批发单价（元）
5
批发量（kg）
①
②
第3题图（1）
O
6
2
40
日最高销量（kg）
80
零售价（元）
第3题图（2）
4
8
（6，80）
（7，40）
金额w（元）
O
批发量m（kg）
300
200
100
20
40
60
2
第5题图
第3题图
y
x
O
B
A
第4题图
O
y
x
2
第2题图
y(升)
18
17
x(分钟)
8
2
12
O
第6题图
第3题图
第2题图
图15
60
40
40
150
30
单位：cm
A
B
B
0
20
0.2
0.3
1.2
B
y1
y2=0.005x+0.3
x(台)
y(万元)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网