三角形与四边形
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
三角形与四边形
一、学习指引
1.知识要点:
三角形的性质,全等三角形的定义、判定和性质,结合等腰三角形、直角三角形以及平行四边形(含矩形、菱形、正方形),梯形等性质的应用,中位线的应用.
2.方法指导:
(1)处理有关三角形和四边形的问题,常转化成基本图形来考虑.
(2)解题过程中常需添加辅助线.
(3)折叠问题中应重视轴对称知识的应用.
二、典型例题
例1.如图,已知边长为5的等边三角形ABC纸片,点E在
AC边上,点F在AB边上,沿着EF折叠,使点A落在
BC边上的点D的位置,且,则CE的长是( )
A. B.
C. D.
例2.如图,O为□ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=12,则S△DOE的值为 ( )
A.1 B. C.2 D.
例3.如图,已知每个小方格的边长为1,A、B、C都在小方格的顶点
上,则点C到AB所在直线的距离等于 .
例4.(07湖州)如图,点A是5×5网格图形中的一个格点(小正方形的顶点),图中每个小正方形的边长为1,以A为其中的一个顶点,面积等于的格点等腰直角三角形(三角形的三个顶点都是格点)的个数是( )
A.10个 B.12个 C.14个 D.16个
例5.(2010山东威海)在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2010个正方形的面积为( )
A. B.
C. D.
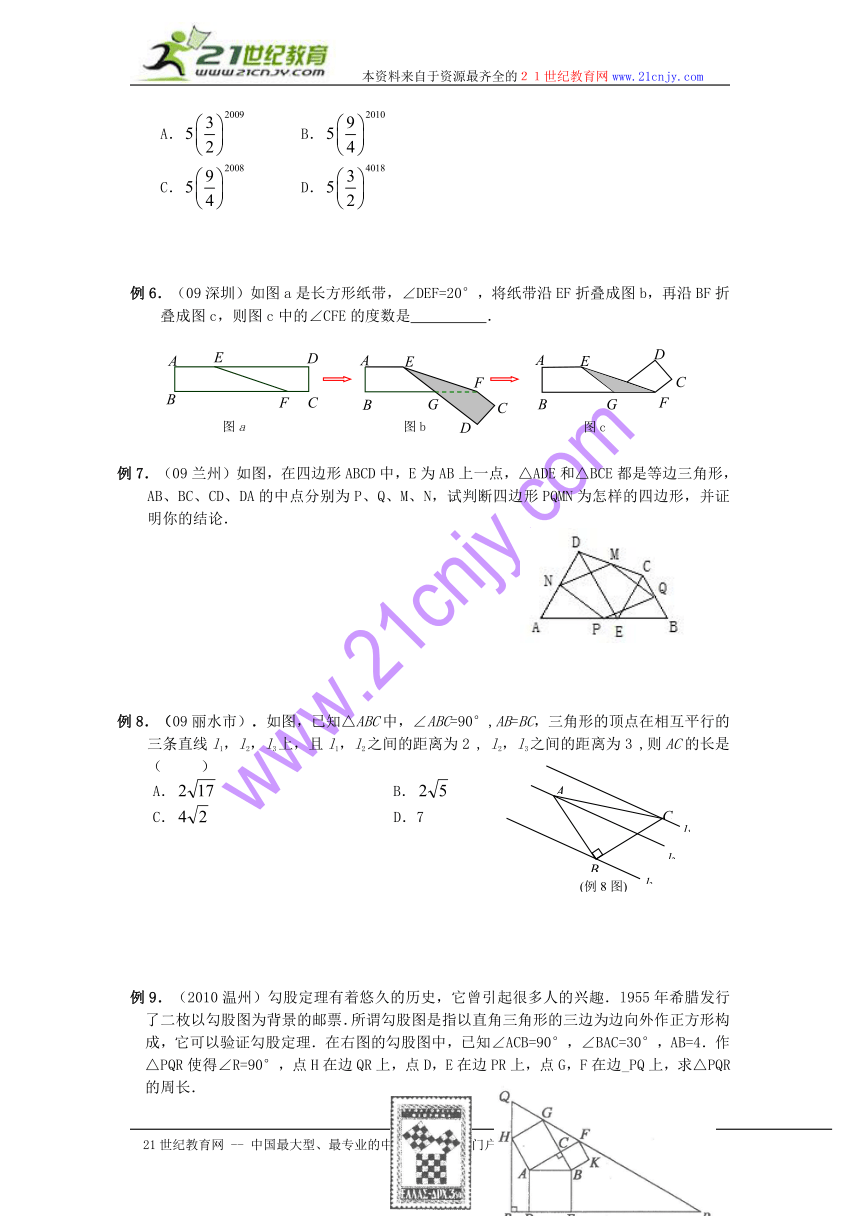
例6.(09深圳)如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是 .
例7.(09兰州)如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,试判断四边形PQMN为怎样的四边形,并证明你的结论.
例8.(09丽水市).如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2 , l2,l3之间的距离为3 ,则AC的长是( )
A. B.
C. D.7
例9.(2010温州)勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边_PQ上,求△PQR的周长.
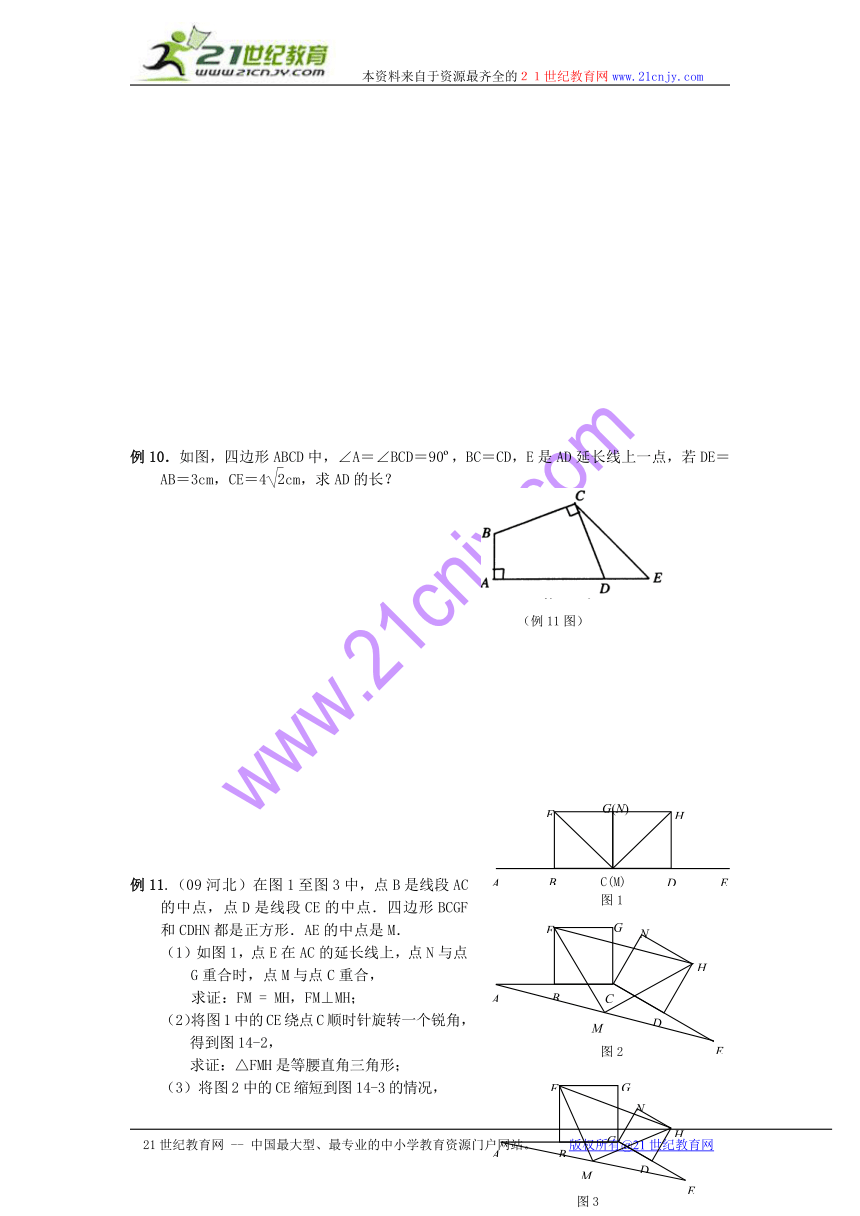
例10.如图,四边形ABCD中,∠A=∠BCD=90 ,BC=CD,E是AD延长线上一点,若DE=AB=3cm,CE=4cm,求AD的长?
例11.(09河北)在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.
(1)如图1,点E在AC的延长线上,点N与点
G重合时,点M与点C重合,
求证:FM = MH,FM⊥MH;
(2)将图1中的CE绕点C顺时针旋转一个锐角,
得到图14-2,
求证:△FMH是等腰直角三角形;
(3)将图2中的CE缩短到图14-3的情况,
△FMH还是等腰直角三角形吗?(不必
说明理由)
三角形与四边形同步练习
【基础巩固】
1.(2010山东烟台)将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2= 。
2.(2009湖州)如图,已知在中,,,分别以,为直径作半圆,面积分别记为,,则+的值等于 .
3.(2009湖州)如图,已知矩形,将沿对角线折叠,记点的对应点为′,若′=20°,则的度数为 _.
4.(09淄博)如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,若EF=3,则梯形ABCD的周长为( )
A.9 B.10.5 C.12 D.15
5.(09淄博市)矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为( )
A. 8 B. C. 4 D.
6.如图,在由24个边长都为1的小正三角形的网格中,点是正六边形的一个顶点,以点为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长 .
7.(2010湖州)请你在如图所示的12×12 的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的 个格点.
8.如图,∠AOB=60°,过OA上到点O的距离分别为1,3,5, 7,
9,11,…的点作OA的垂线与OB相交,得到并标出一组黑色
梯形,它们的面积分别为,,,,….观察图中的规
律,求出第100个黑色梯形的面积=_______________.
9.(09江苏)如图,在梯形中,两点在边上,且四边形是平行四边形.
(1)与有何等量关系?请说明理由;
(2)当时,求证:□是矩形.
【能力拓展】
10.(09 江苏)如图,已知是梯形的中位线,
的面积为,则梯形的面积为
cm2.
11. 如图,在平行四边形ABCD中,A1,A2,A3,A4和B1,B2,B3,B4分
别是AB和DC的五等分点,C1,C2和D1,D2分别是AD和BC的三等分点,若四边形C1A4D2B1的面积为1,则SABCD= .
12.(09年宜宾)已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为___________
13.如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么∶= 。
14. 如图,所示的阴影部分由方格纸上3个小方格组成,我们
称这样的图案为L形,那么小方格组成的方格纸上可
以画出不同位置的L形图案个数是( )
A.16 B.32 C.48 D.64
15.(09吉林)两个长为2cm,宽为1cm的长方形,摆放在直线上(如图①),=2cm,将长方形绕着点顺时针旋转角,将长方形绕着点逆时针旋转相同的角度.
(1)当旋转到顶点、重合时,连接(如图②),求点到的距离;
(2)当时(如图③),求证:四边形为正方形.
例题与同步练习参考答案
三角形与四边形(典型例题)
例1. D . 例2. B 例3. . 例4. D. 例5.D. 例6. 120°.
例7. 证明:如图,连结AC.BD.
∵ PQ为△ABC的中位线,
∴ PQ AC.同理 MNAC.
∴ MNPQ,
∴ 四边形PQMN为平行四边形.在△AEC和△DEB中,
AE=DE,EC=EB,∠AED=60°=∠CEB,
即 ∠AEC=∠DEB.
∴ △AEC≌△DEB.∴ AC=BD.∴ PQ=AC=BD=PN ∴ □PQMN为菱形.
例8. A.
例9.
例10. 5cm.
例11. (1)证明:∵四边形BCGF和CDHN都是正方形,
又∵点N与点G重合,点M与点C重合,
∴FB = BM = MG = MD = DH,∠FBM =∠MDH = 90°.
∴△FBM ≌ △MDH.
∴FM = MH.
∵∠FMB =∠DMH = 45°,∴∠FMH = 90°.
∴FM⊥HM.
(2)证明:连接MB.MD,如图2,设FM与AC交于点P.
∵B.D.M分别是AC.CE.AE的中点,
∴MD∥BC,且MD = BC = BF;MB∥CD,
且MB=CD=DH.
∴四边形BCDM是平行四边形.∴ ∠CBM =∠CDM.
又∵∠FBP =∠HDC,∴∠FBM =∠MDH.∴△FBM ≌ △MDH.
∴FM = MH,且∠MFB =∠HMD.∴∠FMH =∠FMD-∠HMD =∠APM-∠MFB =∠FBP = 90°.∴△FMH是等腰直角三角形.
(3)是.
三角形与四边形(同步练习)
【基础巩固】
1. 90 . 2. . 3. . 4.C. 5.B . 6. . 7.12 8. 796. 9. 略.
【能力拓展】
10. 16. 11. 12.4.5. 13. 1:8 14. C.
15.解:(1)cm,
是等边三角形.
又cm,
.
如图②作于点.
cm.
点到的距离为cm.(2)
四边形是矩形.
又, 矩形是正方形.
A
B
C
D
E
F
(例1图)
(例2图)
B
A
C
(例3图)
A
(例4图)
(例5图)
A
DA
C
BA
EA
CA
BA
FA
DA
C
DBA
EA
FCA
GBA
A
BA
EA
FCA
GBA
A
图a
图b
图c
(例8图)
l1
l2
l3
A
C
B
(例11图)
图1
A
H
C(M)
D
E
B
F
G(N)
G
图2
A
H
C
D
E
B
F
N
M
A
H
C
D
E
图3
B
F
G
M
N
(第1题)
(第3题)
C′
A
D
C
B
20°
(第2题)
C
A
B
S1
S2
A
B
C
D
E
F
P
(第4题)
A
B
C
D
E
G
F
(第5题)
F
(第7题)
P
(第6题)
(第8题)
A
D
C
F
E
B
A
D
E
B
C
F
(第10题)
(第13题)
(第12题)
(第11题)
(第14题)
图②
A
D
B
C
G
E
F
l
图①
A
D
B
C
H
G
E
F
l
图③
A
D
M
C
H
G
E
F
l
B
N
(第15题)
(H)
图2
A
H
C
D
E
B
F
G
N
M
P
图②
A
(H)
B
C
G
E
F
l
图③
A
D
M
C
H
G
E
F
l
B
N
图②
A
D
B
C
G
E
F
l
K
45°
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
三角形与四边形
一、学习指引
1.知识要点:
三角形的性质,全等三角形的定义、判定和性质,结合等腰三角形、直角三角形以及平行四边形(含矩形、菱形、正方形),梯形等性质的应用,中位线的应用.
2.方法指导:
(1)处理有关三角形和四边形的问题,常转化成基本图形来考虑.
(2)解题过程中常需添加辅助线.
(3)折叠问题中应重视轴对称知识的应用.
二、典型例题
例1.如图,已知边长为5的等边三角形ABC纸片,点E在
AC边上,点F在AB边上,沿着EF折叠,使点A落在
BC边上的点D的位置,且,则CE的长是( )
A. B.
C. D.
例2.如图,O为□ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=12,则S△DOE的值为 ( )
A.1 B. C.2 D.
例3.如图,已知每个小方格的边长为1,A、B、C都在小方格的顶点
上,则点C到AB所在直线的距离等于 .
例4.(07湖州)如图,点A是5×5网格图形中的一个格点(小正方形的顶点),图中每个小正方形的边长为1,以A为其中的一个顶点,面积等于的格点等腰直角三角形(三角形的三个顶点都是格点)的个数是( )
A.10个 B.12个 C.14个 D.16个
例5.(2010山东威海)在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2010个正方形的面积为( )
A. B.
C. D.
例6.(09深圳)如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是 .
例7.(09兰州)如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,试判断四边形PQMN为怎样的四边形,并证明你的结论.
例8.(09丽水市).如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2 , l2,l3之间的距离为3 ,则AC的长是( )
A. B.
C. D.7
例9.(2010温州)勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边_PQ上,求△PQR的周长.
例10.如图,四边形ABCD中,∠A=∠BCD=90 ,BC=CD,E是AD延长线上一点,若DE=AB=3cm,CE=4cm,求AD的长?
例11.(09河北)在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.
(1)如图1,点E在AC的延长线上,点N与点
G重合时,点M与点C重合,
求证:FM = MH,FM⊥MH;
(2)将图1中的CE绕点C顺时针旋转一个锐角,
得到图14-2,
求证:△FMH是等腰直角三角形;
(3)将图2中的CE缩短到图14-3的情况,
△FMH还是等腰直角三角形吗?(不必
说明理由)
三角形与四边形同步练习
【基础巩固】
1.(2010山东烟台)将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2= 。
2.(2009湖州)如图,已知在中,,,分别以,为直径作半圆,面积分别记为,,则+的值等于 .
3.(2009湖州)如图,已知矩形,将沿对角线折叠,记点的对应点为′,若′=20°,则的度数为 _.
4.(09淄博)如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P,若EF=3,则梯形ABCD的周长为( )
A.9 B.10.5 C.12 D.15
5.(09淄博市)矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为( )
A. 8 B. C. 4 D.
6.如图,在由24个边长都为1的小正三角形的网格中,点是正六边形的一个顶点,以点为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长 .
7.(2010湖州)请你在如图所示的12×12 的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的 个格点.
8.如图,∠AOB=60°,过OA上到点O的距离分别为1,3,5, 7,
9,11,…的点作OA的垂线与OB相交,得到并标出一组黑色
梯形,它们的面积分别为,,,,….观察图中的规
律,求出第100个黑色梯形的面积=_______________.
9.(09江苏)如图,在梯形中,两点在边上,且四边形是平行四边形.
(1)与有何等量关系?请说明理由;
(2)当时,求证:□是矩形.
【能力拓展】
10.(09 江苏)如图,已知是梯形的中位线,
的面积为,则梯形的面积为
cm2.
11. 如图,在平行四边形ABCD中,A1,A2,A3,A4和B1,B2,B3,B4分
别是AB和DC的五等分点,C1,C2和D1,D2分别是AD和BC的三等分点,若四边形C1A4D2B1的面积为1,则SABCD= .
12.(09年宜宾)已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为___________
13.如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么∶= 。
14. 如图,所示的阴影部分由方格纸上3个小方格组成,我们
称这样的图案为L形,那么小方格组成的方格纸上可
以画出不同位置的L形图案个数是( )
A.16 B.32 C.48 D.64
15.(09吉林)两个长为2cm,宽为1cm的长方形,摆放在直线上(如图①),=2cm,将长方形绕着点顺时针旋转角,将长方形绕着点逆时针旋转相同的角度.
(1)当旋转到顶点、重合时,连接(如图②),求点到的距离;
(2)当时(如图③),求证:四边形为正方形.
例题与同步练习参考答案
三角形与四边形(典型例题)
例1. D . 例2. B 例3. . 例4. D. 例5.D. 例6. 120°.
例7. 证明:如图,连结AC.BD.
∵ PQ为△ABC的中位线,
∴ PQ AC.同理 MNAC.
∴ MNPQ,
∴ 四边形PQMN为平行四边形.在△AEC和△DEB中,
AE=DE,EC=EB,∠AED=60°=∠CEB,
即 ∠AEC=∠DEB.
∴ △AEC≌△DEB.∴ AC=BD.∴ PQ=AC=BD=PN ∴ □PQMN为菱形.
例8. A.
例9.
例10. 5cm.
例11. (1)证明:∵四边形BCGF和CDHN都是正方形,
又∵点N与点G重合,点M与点C重合,
∴FB = BM = MG = MD = DH,∠FBM =∠MDH = 90°.
∴△FBM ≌ △MDH.
∴FM = MH.
∵∠FMB =∠DMH = 45°,∴∠FMH = 90°.
∴FM⊥HM.
(2)证明:连接MB.MD,如图2,设FM与AC交于点P.
∵B.D.M分别是AC.CE.AE的中点,
∴MD∥BC,且MD = BC = BF;MB∥CD,
且MB=CD=DH.
∴四边形BCDM是平行四边形.∴ ∠CBM =∠CDM.
又∵∠FBP =∠HDC,∴∠FBM =∠MDH.∴△FBM ≌ △MDH.
∴FM = MH,且∠MFB =∠HMD.∴∠FMH =∠FMD-∠HMD =∠APM-∠MFB =∠FBP = 90°.∴△FMH是等腰直角三角形.
(3)是.
三角形与四边形(同步练习)
【基础巩固】
1. 90 . 2. . 3. . 4.C. 5.B . 6. . 7.12 8. 796. 9. 略.
【能力拓展】
10. 16. 11. 12.4.5. 13. 1:8 14. C.
15.解:(1)cm,
是等边三角形.
又cm,
.
如图②作于点.
cm.
点到的距离为cm.(2)
四边形是矩形.
又, 矩形是正方形.
A
B
C
D
E
F
(例1图)
(例2图)
B
A
C
(例3图)
A
(例4图)
(例5图)
A
DA
C
BA
EA
CA
BA
FA
DA
C
DBA
EA
FCA
GBA
A
BA
EA
FCA
GBA
A
图a
图b
图c
(例8图)
l1
l2
l3
A
C
B
(例11图)
图1
A
H
C(M)
D
E
B
F
G(N)
G
图2
A
H
C
D
E
B
F
N
M
A
H
C
D
E
图3
B
F
G
M
N
(第1题)
(第3题)
C′
A
D
C
B
20°
(第2题)
C
A
B
S1
S2
A
B
C
D
E
F
P
(第4题)
A
B
C
D
E
G
F
(第5题)
F
(第7题)
P
(第6题)
(第8题)
A
D
C
F
E
B
A
D
E
B
C
F
(第10题)
(第13题)
(第12题)
(第11题)
(第14题)
图②
A
D
B
C
G
E
F
l
图①
A
D
B
C
H
G
E
F
l
图③
A
D
M
C
H
G
E
F
l
B
N
(第15题)
(H)
图2
A
H
C
D
E
B
F
G
N
M
P
图②
A
(H)
B
C
G
E
F
l
图③
A
D
M
C
H
G
E
F
l
B
N
图②
A
D
B
C
G
E
F
l
K
45°
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
