图形变换专题复习
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
图形变换
一、学习指引
1.知识要点:
轴对称的基本性质:_______________________________________________;
平移的基本性质:_________________________________________________;
旋转的基本性质:_________________________________________________;
2.方法指导:
轴对称、平移、旋转和相似是图形的四种基本变换.
通过平移或旋转变换可以将一个图形或图形的某一部分平移或旋转到一个适当的位置,组成有利于解题的新图形,即将原来比较分散的已知条件通过平移或旋转变换而集中在一起.
利用轴对称变换解决问题时,常会用到角平分线、线段中点、等腰(边)三角形的知识.
二、典型例题
例1 .如图3是小华画的正方形风筝图案,他以图中的对角线AB为对称轴,在对角线的下方再画一个三角形,使得新的风筝图案成为轴对称图形,若下列有一图形为此对称图形,则此图为
例2.如图,是由大小一样的正方形组成网格,△ABC的三个顶点落在小正方形的顶点上,请在网格上画出三个顶点都落在小正方形的顶点上,且与△ABC成轴对称的所有位置不同的三角形.(下图备用)
例3. 在平面直角坐标系中,O为坐标原点.
(1)已知点A(3,1),连结OA,平移线段OA,使点O落在点B.设点A落在点C,作如下探究:
探究一:若点B的坐标为(1,2),请在图1中作出平移后的像,则点C的坐标是 ;连结AC,BO,请判断O,A,C,B四点构成的图形的形状,并说明理由;
探究二:若点B的坐标为(6,2),按探究一的方法,判断O,A,B,C四点构成的图形的形状(直接写出结论即可).
(2)通过上面的探究,请直接回答下列问题:
①若已知三点A (a,b),B(c,d),C (a+c,b+d),顺次连结O,A,C,B,请判断所得到的图形的形状;
②在①的条件下,如果所得到的图形是菱形或者是正方形,请选择一种情况,写出a,b,c,d应满足的关系式.
例4.实验与推理如图14―1,14―2,四边形ABCD是正方形,M是AB延长线上一点。直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F。
⑴如图14―1,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是 ;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ;
③请证明你的上述两猜想。
⑵如图14―2,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系。
例5. 正方形ABCD的边长为8,M在DC上,且DM=2,N是对角线上的一动点,求DN+MN的最小值
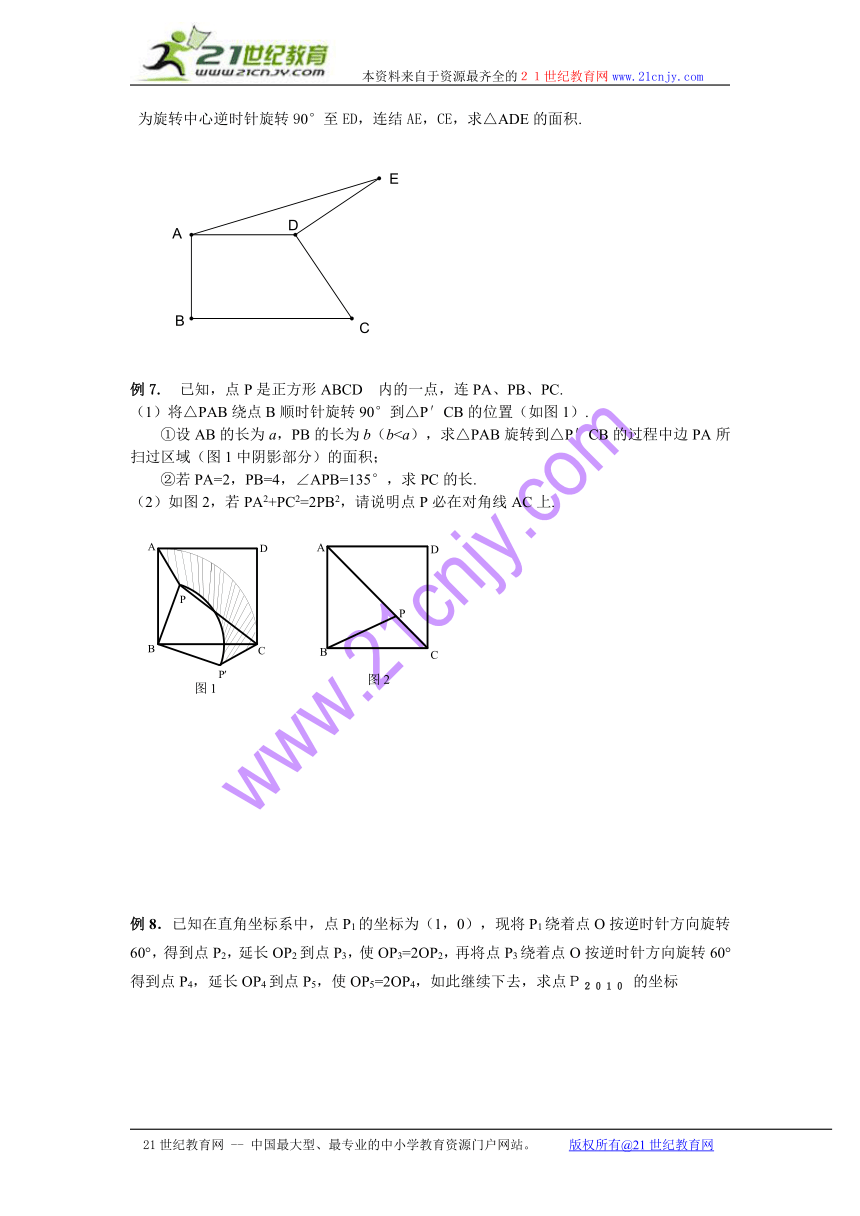
例6. 如图, 在梯形ABCD中,AD∥BC,∠DAB=∠B=90°,AD=4,BC=5,将腰CD以D为旋转中心逆时针旋转90°至ED,连结AE,CE,求△ADE的面积.
例7. 已知,点P是正方形ABCD 内的一点,连PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1).
①设AB的长为a,PB的长为b(b②若PA=2,PB=4,∠APB=135°,求PC的长.
(2)如图2,若PA2+PC2=2PB2,请说明点P必在对角线AC上.
例8.已知在直角坐标系中,点P1的坐标为(1,0),现将P1绕着点O按逆时针方向旋转60°,得到点P2,延长OP2到点P3,使OP3=2OP2,再将点P3绕着点O按逆时针方向旋转60°得到点P4,延长OP4到点P5,使OP5=2OP4,如此继续下去,求点P2010 的坐标
例9. 在等腰梯形ABCD中,AB∥DC,∠A=45°,AB=10 cm,CD=4 cm.等腰直角三角形PMN的斜边MN=10 cm,A点与N点重合,MN和AB在一条直线上,设等腰梯形ABCD不动,等腰直角三角形PMN沿AB所在直线以1 cm/s的速度向右移动,直到点N与点B重合为止.
(1)等腰直角三角形PMN在整个移动过程中与等腰梯形AB ( http: / / www.21cnjy.com / )CD重叠部分的形状由_____________变化为__________;
(2)设当等腰直角三角形PMN移动x(s)时,等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积为y(cm2),求y与x之间的函数表达式;
(3)当x=4(s),求等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积.
图形变换同步练习
【基础巩固】
1. 下列图形中,你认为既是中心对称图形又是轴对称图形的是( )
2.在5×5方格纸中将图(1)中的图形N平移后的位置如图(2)中所示,那么正确的平移方法是 ( )
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
3.一个汽车牌照在镜子中的像为 ,则该汽牌照号码为 .
4.分析图中(1)、(2)、(4)中阴影部分的分布规律,按此规律在图(3)中画出其中的阴影部分.
(1) (2) (3) (4)
5.上右图是万花筒的一个图案,图中所有小三角形均是全等三角形,其中把菱形ABCD以A为中心旋转多少度后可得图中另一阴影的菱形( )
A.顺时针旋转60° B. 顺时针旋转120°
C.逆时针旋转60° D. 逆时针旋转120°
6.如图,把一张长方形纸条沿折叠,若,则 .
7.四张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180 后得到如图(2)所示,那么她所旋转的牌从左数起是( )
A.第一张 B.第二张 C.第三张 D.第四张
8.将一副三角板按如图1位置摆放,使得两块三角板
的直角边AC和MD重合.已知AB=AC=8 cm,将
△MED绕点A(M)逆时针旋转60°后(图2),两个三角形重叠(阴影)部分的面积约是 ▲ cm2 (结果 精确到0.1,).
9.如图,在梯形中,∥,的长为4,,已知点、的坐标分别为(1,0)和(2,-3).
⑴ 求点的坐标;
⑵ 取点(2,-1),联结并延长交于,试猜想与之间的位置关系,并证明你的结论;
⑶ 将梯形绕点旋转后成梯形,画出梯形.
10.如图,在直角梯形纸片中,,,,将纸片沿过点的直线折叠,使点落在边上的点处,折痕为.连接并展开纸片.
(1)求证:四边形是正方形;
(2)取线段的中点,连接,如果,试说明四边形是等腰梯形.
【能力拓展】
11.如图,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为______________.
12.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.
在自然界和日常生活中,大量地存在这种图形变换(如图1).结
合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( )
A.对应点连线与对称轴垂直
B.对应点连线被对称轴平分
C.对应点连线被对称轴垂直平分
D.对应点连线互相平行
13.∠MON内有一点P,它关于OM、ON的对称点分别是
A、B,若∠MON=45°,则△AOB必是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
14. 如图,菱形纸片ABCD的一内角为60°.边长为2, 将它绕对角线的交点O顺时针旋转90°后到A′B′C′D′位置,则旋转前后两菱形重叠部分多边形的周长为_____________
15.正方形绿化场地拟种植两种不同颜色的花卉,要求种植的花卉能组成轴对称或中心对称图案.下面是三种不同设计方案中的一部分,请把图①、图②补成既是轴对称图形,又是中心对称图形,并画出一条对称轴;把图③补成只是中心对称图形,并把中心标上字母P.(在你所设计的图案中用阴影部分和非阴影部分表示两种不同颜色的花卉.)
16.如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).
(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
17. 如图12,在直角坐标系中,已知点的坐标为(1,0),将线段绕原点O沿逆时针方向旋转45,再将其延长到,使得,得到线段;又将线段绕原点O沿逆时针方向旋转45,再将其延长到,使得,得到线段,如此下去,得到线段,,…,.
(1)写出点M5的坐标;
(2)求的周长;
(3)我们规定:把点(0,1,2,3…)
的横坐标,纵坐标都取绝对值后得到的新坐标
称之为点的“绝对坐标”.根据图中点
的分布规律,请你猜想点的“绝对坐标”,并写出来.
例题与同步练习参考答案
图形变换(典型例题)
例1 C
例2
例3. (1)探究一: C (4,3),四边形OACB为平行四边形,
理由如下:由平移可知,OA∥BC且OA=BC,所以四边形OACB为平行四边形.
探究二:线段
(2) ①平行四边形或线段
②菱形:a2+b2=c2+d2 (a=-c,b=-d除外)正方形:或
例4.(1)①DE=EF;②NE=BF。
③证明:∵四边形ABCD是正方形,N,E分别为AD,AB的中点,∴DN=EB
∵BF平分∠CBM,AN=AE,∴∠DNE=∠EBF=90°+45°=135°
∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF
∴△DNE≌△EBF,∴ DE=EF,NE=BF
(2)在DA边上截取DN=EB(或截取AN=AE),连结NE,点N就使得NE=BF成立(图略)此时,DE=EF。
例5. 10 例6. 2
例7 (1)①S阴影=
②连结PP′,证△PBP′为等腰直角三角形,从而PC=6;
(2)将△PAB绕点B顺时针旋转90°到△P′CB的位置,由勾股逆定理证出∠P′CP=90°,再证∠BPC+∠APB=180°,即点P在对角线AC上.
例8. .
例9. (1) 等腰直角三角形 等腰梯形
(2)等腰直角三角形PMN在整个移动过程中与等腰梯形ABCD重叠部分图形的形状可分为以下两种情况:
① 当0重叠部分的形状为等腰直角三角形EAN(如图①).
此时AN=x(cm),过点E作EH⊥AB于点H,则EH平分AN, ∴EH=AN=x.
y=S△ANE=AN·EH=x·x=x2.
②当6此时AN=x(cm),∵ ∠PNM=∠B=45°,∴EN∥BC.
∵ CE∥BN,∴四边形ENBC是平行四边形,CE=BN=10-x,DE=4-(10-x)=x-6.
过点D作DF⊥AB于F,过点C作CG⊥AB于G,则AF=BG,DF=AF=(10-4)=3.
∴ y=S梯形ANED=(DE+AN)·DF=(x-6+x)×3=3x-9.
(3) 当等腰直角三角形PMN移动到PN边经过点D时,移动时间为6(s).
∴ 当x=4(s)时,y=x2=×42=4.
∴ 当x=4(s)时,等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积是4 cm2.
图形变换(同步练习)
【基础巩固】
1.A 2.C 3.SM17963 4.
5.D 6.64° 7.A
8.20.3
9.⑴ ∵ ,
∴ ,∴ 点的坐标为(4,-3).
⑵ 猜想:. 证明:连接BE并延长交轴于点H.
∵ 、坐标分别为(2,-3),(2,-1),
∴ 轴,(2,0)
∴ ,,
,
∴ ≌,
∴ ,
又∵ ,
∴ ,
∴ .
⑶ 如图,梯形绕点旋转后成梯形.
10.证明:(1),,.
由沿折叠后与重合,知,.
四边形是矩形,且邻边相等.
四边形是正方形.
(2),且,四边形是梯形.
四边形是正方形,,.
又点为的中点,.连接.
在与中,,,,
,.
,,四边形是平行四边形.
...
四边形是等腰梯形.
注:第(2)小题也可过点作,垂足为点,证.
【能力拓展】
11. 12.B 13.D 14.8(-1)
15.
16. 解:(1)证明:在ΔABC和ΔAEP中
∵∠ABC=∠AEP,∠BAC=∠EAP
∴ ∠ACB=∠APE
在ΔABC中,AB=BC
∴∠ACB=∠BAC
∴ ∠EPA=∠EAP
(2)答:□ APCD是矩形
∵四边形APCD是平行四边形
∴ AC=2EA, PD=2EP
∵ 由(1)知 ∠EPA=∠EAP
∴ EA=EP
则 AC=PD
∴□APCD是矩形
(3)答: EM=EN
∵EA=EP ∴ ∠EPA=90°- α
∴∠EAM=180°-∠EPA=180°-(90°- α)=90°+ α
由(2)知∠CPB=90°,F是BC的中点,∴ FP=FB
∴∠FPB=∠ABC=α
∴ ∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°- α+α=90°+α
∴ ∠EAM=∠EPN
∵ ∠AEP绕点E顺时针旋转适当的角度,得到∠MEN
∴ ∠AEP=∠MEN
∴∠AEP- ∠AEN=∠MEN-∠AEN 即 ∠MEA=∠NEP
∴ ΔEAM≌ΔEPN ∴ EM=EN
17. 解:(1)M5(―4,―4)(2)由规律可知,,, ∴的周长是(3)解法一:由题意知,旋转8次之后回到轴的正半轴,在这8次旋转中,点分别落在坐标象限的分角线上或轴或轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,点的“绝对坐标”可分三类情况:
令旋转次数为
1 当点M在x轴上时: M0(),M4(),M8(),M12(),…,
即:点的“绝对坐标”为()。
2 当点M在y轴上时: M2,M6,M10,M14,……,
即:点的“绝对坐标”为。
3 当点M在各象限的分角线上时:M1,M3,M5,M7,……,即:的“绝对坐标”为。
(A)
(B)
(D)
(C)
(图3)
A
B
y
B
A
O
x
图1
1
x
O
A
B
y
图2
1
_
N
_
M
_
D
_
C
_
B
_
A
图1
图2
图图(1) 图(2)
E
D
A
G
1
B
F
C
(第8题)
E
C
B
D
A
G
F
A
B
C
D
HYPERLINK "http://www./" EMBED Equation.DSMT4
A
C
B
图2
图1
第14题
图①
图②
图③
图1
A
B
D
C
E
P
图2
A
B
D
C
E
P
M
N
F
(图12)
E
C
B
D
A
G
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
图形变换
一、学习指引
1.知识要点:
轴对称的基本性质:_______________________________________________;
平移的基本性质:_________________________________________________;
旋转的基本性质:_________________________________________________;
2.方法指导:
轴对称、平移、旋转和相似是图形的四种基本变换.
通过平移或旋转变换可以将一个图形或图形的某一部分平移或旋转到一个适当的位置,组成有利于解题的新图形,即将原来比较分散的已知条件通过平移或旋转变换而集中在一起.
利用轴对称变换解决问题时,常会用到角平分线、线段中点、等腰(边)三角形的知识.
二、典型例题
例1 .如图3是小华画的正方形风筝图案,他以图中的对角线AB为对称轴,在对角线的下方再画一个三角形,使得新的风筝图案成为轴对称图形,若下列有一图形为此对称图形,则此图为
例2.如图,是由大小一样的正方形组成网格,△ABC的三个顶点落在小正方形的顶点上,请在网格上画出三个顶点都落在小正方形的顶点上,且与△ABC成轴对称的所有位置不同的三角形.(下图备用)
例3. 在平面直角坐标系中,O为坐标原点.
(1)已知点A(3,1),连结OA,平移线段OA,使点O落在点B.设点A落在点C,作如下探究:
探究一:若点B的坐标为(1,2),请在图1中作出平移后的像,则点C的坐标是 ;连结AC,BO,请判断O,A,C,B四点构成的图形的形状,并说明理由;
探究二:若点B的坐标为(6,2),按探究一的方法,判断O,A,B,C四点构成的图形的形状(直接写出结论即可).
(2)通过上面的探究,请直接回答下列问题:
①若已知三点A (a,b),B(c,d),C (a+c,b+d),顺次连结O,A,C,B,请判断所得到的图形的形状;
②在①的条件下,如果所得到的图形是菱形或者是正方形,请选择一种情况,写出a,b,c,d应满足的关系式.
例4.实验与推理如图14―1,14―2,四边形ABCD是正方形,M是AB延长线上一点。直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F。
⑴如图14―1,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是 ;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ;
③请证明你的上述两猜想。
⑵如图14―2,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系。
例5. 正方形ABCD的边长为8,M在DC上,且DM=2,N是对角线上的一动点,求DN+MN的最小值
例6. 如图, 在梯形ABCD中,AD∥BC,∠DAB=∠B=90°,AD=4,BC=5,将腰CD以D为旋转中心逆时针旋转90°至ED,连结AE,CE,求△ADE的面积.
例7. 已知,点P是正方形ABCD 内的一点,连PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1).
①设AB的长为a,PB的长为b(b
(2)如图2,若PA2+PC2=2PB2,请说明点P必在对角线AC上.
例8.已知在直角坐标系中,点P1的坐标为(1,0),现将P1绕着点O按逆时针方向旋转60°,得到点P2,延长OP2到点P3,使OP3=2OP2,再将点P3绕着点O按逆时针方向旋转60°得到点P4,延长OP4到点P5,使OP5=2OP4,如此继续下去,求点P2010 的坐标
例9. 在等腰梯形ABCD中,AB∥DC,∠A=45°,AB=10 cm,CD=4 cm.等腰直角三角形PMN的斜边MN=10 cm,A点与N点重合,MN和AB在一条直线上,设等腰梯形ABCD不动,等腰直角三角形PMN沿AB所在直线以1 cm/s的速度向右移动,直到点N与点B重合为止.
(1)等腰直角三角形PMN在整个移动过程中与等腰梯形AB ( http: / / www.21cnjy.com / )CD重叠部分的形状由_____________变化为__________;
(2)设当等腰直角三角形PMN移动x(s)时,等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积为y(cm2),求y与x之间的函数表达式;
(3)当x=4(s),求等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积.
图形变换同步练习
【基础巩固】
1. 下列图形中,你认为既是中心对称图形又是轴对称图形的是( )
2.在5×5方格纸中将图(1)中的图形N平移后的位置如图(2)中所示,那么正确的平移方法是 ( )
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
3.一个汽车牌照在镜子中的像为 ,则该汽牌照号码为 .
4.分析图中(1)、(2)、(4)中阴影部分的分布规律,按此规律在图(3)中画出其中的阴影部分.
(1) (2) (3) (4)
5.上右图是万花筒的一个图案,图中所有小三角形均是全等三角形,其中把菱形ABCD以A为中心旋转多少度后可得图中另一阴影的菱形( )
A.顺时针旋转60° B. 顺时针旋转120°
C.逆时针旋转60° D. 逆时针旋转120°
6.如图,把一张长方形纸条沿折叠,若,则 .
7.四张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180 后得到如图(2)所示,那么她所旋转的牌从左数起是( )
A.第一张 B.第二张 C.第三张 D.第四张
8.将一副三角板按如图1位置摆放,使得两块三角板
的直角边AC和MD重合.已知AB=AC=8 cm,将
△MED绕点A(M)逆时针旋转60°后(图2),两个三角形重叠(阴影)部分的面积约是 ▲ cm2 (结果 精确到0.1,).
9.如图,在梯形中,∥,的长为4,,已知点、的坐标分别为(1,0)和(2,-3).
⑴ 求点的坐标;
⑵ 取点(2,-1),联结并延长交于,试猜想与之间的位置关系,并证明你的结论;
⑶ 将梯形绕点旋转后成梯形,画出梯形.
10.如图,在直角梯形纸片中,,,,将纸片沿过点的直线折叠,使点落在边上的点处,折痕为.连接并展开纸片.
(1)求证:四边形是正方形;
(2)取线段的中点,连接,如果,试说明四边形是等腰梯形.
【能力拓展】
11.如图,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为______________.
12.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.
在自然界和日常生活中,大量地存在这种图形变换(如图1).结
合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( )
A.对应点连线与对称轴垂直
B.对应点连线被对称轴平分
C.对应点连线被对称轴垂直平分
D.对应点连线互相平行
13.∠MON内有一点P,它关于OM、ON的对称点分别是
A、B,若∠MON=45°,则△AOB必是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
14. 如图,菱形纸片ABCD的一内角为60°.边长为2, 将它绕对角线的交点O顺时针旋转90°后到A′B′C′D′位置,则旋转前后两菱形重叠部分多边形的周长为_____________
15.正方形绿化场地拟种植两种不同颜色的花卉,要求种植的花卉能组成轴对称或中心对称图案.下面是三种不同设计方案中的一部分,请把图①、图②补成既是轴对称图形,又是中心对称图形,并画出一条对称轴;把图③补成只是中心对称图形,并把中心标上字母P.(在你所设计的图案中用阴影部分和非阴影部分表示两种不同颜色的花卉.)
16.如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).
(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
17. 如图12,在直角坐标系中,已知点的坐标为(1,0),将线段绕原点O沿逆时针方向旋转45,再将其延长到,使得,得到线段;又将线段绕原点O沿逆时针方向旋转45,再将其延长到,使得,得到线段,如此下去,得到线段,,…,.
(1)写出点M5的坐标;
(2)求的周长;
(3)我们规定:把点(0,1,2,3…)
的横坐标,纵坐标都取绝对值后得到的新坐标
称之为点的“绝对坐标”.根据图中点
的分布规律,请你猜想点的“绝对坐标”,并写出来.
例题与同步练习参考答案
图形变换(典型例题)
例1 C
例2
例3. (1)探究一: C (4,3),四边形OACB为平行四边形,
理由如下:由平移可知,OA∥BC且OA=BC,所以四边形OACB为平行四边形.
探究二:线段
(2) ①平行四边形或线段
②菱形:a2+b2=c2+d2 (a=-c,b=-d除外)正方形:或
例4.(1)①DE=EF;②NE=BF。
③证明:∵四边形ABCD是正方形,N,E分别为AD,AB的中点,∴DN=EB
∵BF平分∠CBM,AN=AE,∴∠DNE=∠EBF=90°+45°=135°
∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF
∴△DNE≌△EBF,∴ DE=EF,NE=BF
(2)在DA边上截取DN=EB(或截取AN=AE),连结NE,点N就使得NE=BF成立(图略)此时,DE=EF。
例5. 10 例6. 2
例7 (1)①S阴影=
②连结PP′,证△PBP′为等腰直角三角形,从而PC=6;
(2)将△PAB绕点B顺时针旋转90°到△P′CB的位置,由勾股逆定理证出∠P′CP=90°,再证∠BPC+∠APB=180°,即点P在对角线AC上.
例8. .
例9. (1) 等腰直角三角形 等腰梯形
(2)等腰直角三角形PMN在整个移动过程中与等腰梯形ABCD重叠部分图形的形状可分为以下两种情况:
① 当0
此时AN=x(cm),过点E作EH⊥AB于点H,则EH平分AN, ∴EH=AN=x.
y=S△ANE=AN·EH=x·x=x2.
②当6
∵ CE∥BN,∴四边形ENBC是平行四边形,CE=BN=10-x,DE=4-(10-x)=x-6.
过点D作DF⊥AB于F,过点C作CG⊥AB于G,则AF=BG,DF=AF=(10-4)=3.
∴ y=S梯形ANED=(DE+AN)·DF=(x-6+x)×3=3x-9.
(3) 当等腰直角三角形PMN移动到PN边经过点D时,移动时间为6(s).
∴ 当x=4(s)时,y=x2=×42=4.
∴ 当x=4(s)时,等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积是4 cm2.
图形变换(同步练习)
【基础巩固】
1.A 2.C 3.SM17963 4.
5.D 6.64° 7.A
8.20.3
9.⑴ ∵ ,
∴ ,∴ 点的坐标为(4,-3).
⑵ 猜想:. 证明:连接BE并延长交轴于点H.
∵ 、坐标分别为(2,-3),(2,-1),
∴ 轴,(2,0)
∴ ,,
,
∴ ≌,
∴ ,
又∵ ,
∴ ,
∴ .
⑶ 如图,梯形绕点旋转后成梯形.
10.证明:(1),,.
由沿折叠后与重合,知,.
四边形是矩形,且邻边相等.
四边形是正方形.
(2),且,四边形是梯形.
四边形是正方形,,.
又点为的中点,.连接.
在与中,,,,
,.
,,四边形是平行四边形.
...
四边形是等腰梯形.
注:第(2)小题也可过点作,垂足为点,证.
【能力拓展】
11. 12.B 13.D 14.8(-1)
15.
16. 解:(1)证明:在ΔABC和ΔAEP中
∵∠ABC=∠AEP,∠BAC=∠EAP
∴ ∠ACB=∠APE
在ΔABC中,AB=BC
∴∠ACB=∠BAC
∴ ∠EPA=∠EAP
(2)答:□ APCD是矩形
∵四边形APCD是平行四边形
∴ AC=2EA, PD=2EP
∵ 由(1)知 ∠EPA=∠EAP
∴ EA=EP
则 AC=PD
∴□APCD是矩形
(3)答: EM=EN
∵EA=EP ∴ ∠EPA=90°- α
∴∠EAM=180°-∠EPA=180°-(90°- α)=90°+ α
由(2)知∠CPB=90°,F是BC的中点,∴ FP=FB
∴∠FPB=∠ABC=α
∴ ∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°- α+α=90°+α
∴ ∠EAM=∠EPN
∵ ∠AEP绕点E顺时针旋转适当的角度,得到∠MEN
∴ ∠AEP=∠MEN
∴∠AEP- ∠AEN=∠MEN-∠AEN 即 ∠MEA=∠NEP
∴ ΔEAM≌ΔEPN ∴ EM=EN
17. 解:(1)M5(―4,―4)(2)由规律可知,,, ∴的周长是(3)解法一:由题意知,旋转8次之后回到轴的正半轴,在这8次旋转中,点分别落在坐标象限的分角线上或轴或轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,点的“绝对坐标”可分三类情况:
令旋转次数为
1 当点M在x轴上时: M0(),M4(),M8(),M12(),…,
即:点的“绝对坐标”为()。
2 当点M在y轴上时: M2,M6,M10,M14,……,
即:点的“绝对坐标”为。
3 当点M在各象限的分角线上时:M1,M3,M5,M7,……,即:的“绝对坐标”为。
(A)
(B)
(D)
(C)
(图3)
A
B
y
B
A
O
x
图1
1
x
O
A
B
y
图2
1
_
N
_
M
_
D
_
C
_
B
_
A
图1
图2
图图(1) 图(2)
E
D
A
G
1
B
F
C
(第8题)
E
C
B
D
A
G
F
A
B
C
D
HYPERLINK "http://www./" EMBED Equation.DSMT4
A
C
B
图2
图1
第14题
图①
图②
图③
图1
A
B
D
C
E
P
图2
A
B
D
C
E
P
M
N
F
(图12)
E
C
B
D
A
G
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
