直线型几何综合题
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
直线型几何综合题
一、学习指引
1.知识要点:
三角形及四边形的基本性质,特殊三角形、特殊四边形、全等三角形的判定和性质,轴对称、平移、旋转、相似等变换的性质,一次函数图象和性质。
2.方法指导:
(1)解决动态几何型问题的策略:化“动”为“静”——利用运动中特殊点的位置将图形分类;“静”中求“动”——针对各类图形,分别解决动态问题。
(2)解决图形分割问题的思维方式是:从具体问题出发→观察猜想→实验操作→形成方案→严密计算与论证;图形分割问题的解题策略:比较原图形与分割后图形在边、角、面积等方面的变化是解决图形分割问题的着手点;
(3)新概念性几何题解题策略:正确理解问题中的“新概念”,然后抓住 “新概念”的特征,结合相关的数学知识综合解决问题。
2、 典型例题
例1.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程看作时间的函数,其图像可能是( )
(A) (B) (C) (D)
例2.16.如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),
A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已
知点D在第一象限,且是两直线y1=2x+6、y2=2x-6中某
条上的一点,若△APD是等腰Rt△,则点D的坐标为
例3.如图,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着从点A向点B的方向移动(不与点A,B重合),连接DE,得到四边形DMNE.这个四边形的面积变化情况为( )
(A)逐渐增大 (B) 逐渐减小
(C) 始终不变 (D) 先增大后变小
例4.如图1,有一张菱形纸片ABCD,,。
(1) 请沿着AC剪一刀,把它分成两部分,把剪开的两部
分拼成一个平行四边形,在图2中用实数画出你所拼成的平
行四边形;若沿着BD剪开,请在图3中用实线画出拼成的
平行四边形;并直接写出这两个平行四边形的周长。
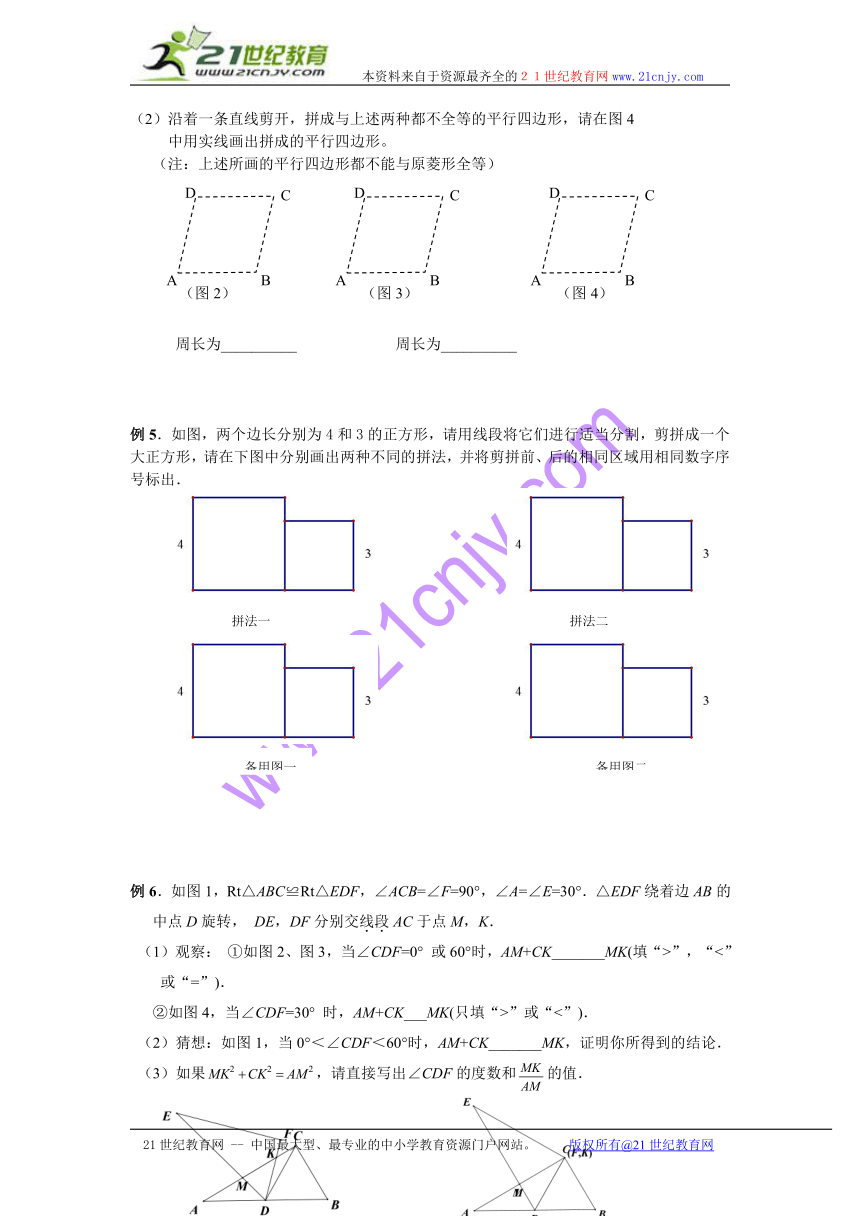
(2)沿着一条直线剪开,拼成与上述两种都不全等的平行四边形,请在图4
中用实线画出拼成的平行四边形。
(注:上述所画的平行四边形都不能与原菱形全等)
周长为__________ 周长为__________
例5.如图,两个边长分别为4和3的正方形,请用线段将它们进行适当分割,剪拼成一个大正方形,请在下图中分别画出两种不同的拼法,并将剪拼前、后的相同区域用相同数字序号标出.
例6.如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果,请直接写出∠CDF的度数和的值.
例7.类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+()=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量” {1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量” {3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
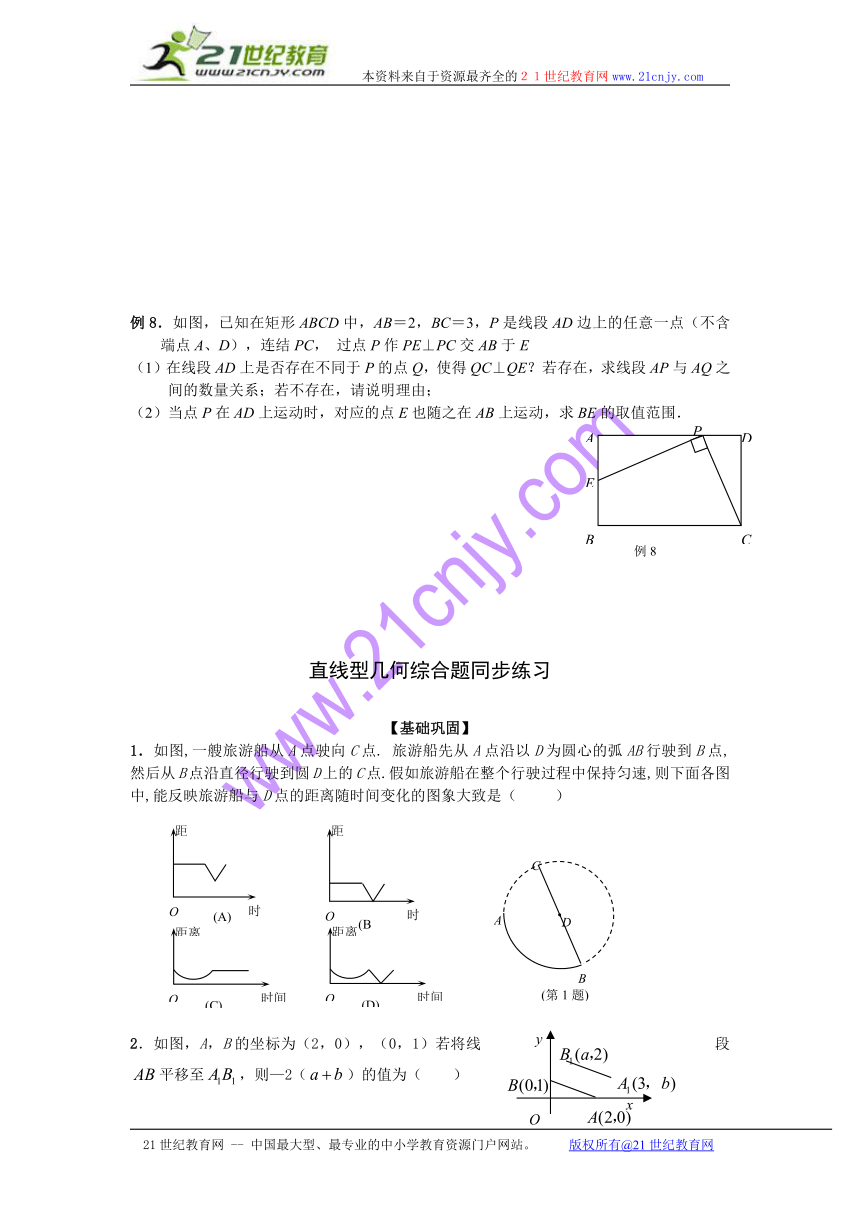
例8.如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连结PC, 过点P作PE⊥PC交AB于E
(1)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求线段AP与AQ之间的数量关系;若不存在,请说明理由;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,求BE的取值范围.
直线型几何综合题同步练习
【基础巩固】
1.如图,一艘旅游船从A点驶向C点. 旅游船先从A点沿以D为圆心的弧AB行驶到B点,然后从B点沿直径行驶到圆D上的C点.假如旅游船在整个行驶过程中保持匀速,则下面各图中,能反映旅游船与D点的距离随时间变化的图象大致是( )
2.如图,A,B的坐标为(2,0),(0,1)若将线段平移至,则—2()的值为( )
A.2 B.3 C.4 D.5
3.如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 ( )
(A)(0,0) (B)(,)
(C)(-,-) (D)(-,-)
4.如图,一个的矩形可以用3种不同的方式分割成2或5或8个小正方形,那么一个的矩形用不同的方式分割后,小正方形的个数可以是
5.如图,在平面直角坐标系中,为原点,四边形是矩形,A(10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是 。
6.如图,将边长为1的正三角形沿轴正方向连续翻转2008次,点依次落在点的位置,则点的横坐标为 .
7.矩形ABCD的边AB=8,AD=6,现将矩形ABCD放在直线l上且沿着l向右作无滑动地翻滚,当它翻滚至类似开始的位置时(如图所示),则顶点A所经过的路线长是_________ .
8.如图,正方形ABCD边长为1,动点P从A点出发,沿正方形的边按逆时针方向运动,当它的运动路程为2009时,点P所在位置为______;当点P所在位置为D点时,点P的运动路程为______(用含自然数n的式子表示).
9.如图,矩形ABCD中,AB=8,BC=6,画出面积不相等的三个菱形,使菱形的顶点都在矩形的边上,并分别求出所画菱形的面积。(下列图形供画图用)
10.(1)请在图①的正方形ABCD内,画出使∠APB=90°的一个点P,并说明理由.
(2)请在图②的正方形ABCD内(含边),画出使∠APB=60°的所有的点P,并说明理由。
(3)如图③,现在一块矩形钢板ABCD,AB=4,BC=3,工人师傅想用它裁出两块全等的、面积最大的△APB和△CPD钢板,且∠APB=∠CPD=60°,请你在图③中画出符合要求的点P和P.
11.如图,四边形ABCD中,AB=AD,CB=CD,但ADCD,我们称这样的四边形为“半菱形”。小明说“‘半菱形’的面积等于两条对角线乘积的一半”。他的说法正确吗?请你判断并证明你的结论.
12.如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5,BC=12,CD=,∠C=45°,点P是BC边上一动点,设PB的长为x.
(1)当x的值为____________时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为____________时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
【能力拓展】
13.如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________.
14.如图,一种电子游戏,电子屏幕上有一正六边形ABCDEF,点P沿直线AB从右向左移动,当出现点P与正六边形六个顶点中的至少两个顶点距离相等时,就会发出警报,则直线AB上会发出警报的点P有( )
A.3个 B.4个 C.5个 D.6个
15.如图,在Rt△ABC中,∠ACB=90°, ∠B =60°,BC=2.点0是AC的中点,过点0的直线l从与AC重合的位置开始,绕点0作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.
(1)①当α=________度时,四边形EDBC是等腰梯形,此时AD的长为_________;
②当α=________度时,四边形EDBC是直角梯形,此时AD的长为_________.
(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.
16. 问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,
过点E作EF∥AB交BC于点F.请按图示数据填空:
四边形DBFE的面积 ,
△EFC的面积 ,
△ADE的面积 .
探究发现
(2)在(1)中,若,,DE与BC间的距离为.请证明.
拓展迁移
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若
△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)
中的结论求△ABC的面积.
例题与同步练习参考答案
直线型几何综合题(典型例题)
例1. A例2. (4,2),(4,14),(,),(,) 例3.C
例4.
例5.
例6.(1)① = ② >
(2)>
证明:作点C关于FD的对称点G,
连接GK,GM,GD,
则CD=GD ,GK = CK,∠GDK=∠CDK,
∵D是AB的中点,∴AD=CD=GD.
∵30°,∴∠CDA=120°,∵∠EDF=60°,∴∠GDM+∠GDK=60°,∠ADM+∠CDK =60°.∴∠ADM=∠GDM,∵DM=DM,∴△ADM≌△GDM,∴GM=AM.∵GM+GK>MK,∴AM+CK>MK.(3)∠CDF=15°,.
例7.(1){3,1}+{1,2}={4,3}. {1,2}+{3,1}={4,3}.
(2)①画图 最后的位置仍是B.
② 证明:由①知,A(3,1),B(4,3),C(1,2)
∴OC=AB==,OA=BC==,
∴四边形OABC是平行四边形.(3){2,3}+{3,2}+{-5,-5}={0, 0}.
例8. (1)当P是AD的中点时,满足条件的点Q不存在;当P不是AD的中点时,总存在这样的点Q满足条件,此时AP+AQ=3 (2) 7/8≦BE<2
直线型几何综合题(同步练习)
【基础巩固】
1.B; 2.D ;3.C ; 4.4或7或9或12或15个小正方形; 5.(4,3)(1,3)(9,3);6. 2008; 7.12π;8.点B;4n+3;
9.
10. (1)如图①,点P为所求(2)如图②,圆上实线部分弧EF为所求②③
(3)如图③,点、为所求
11.
12.(1)3或8 (2)1或11 (3)能构成菱形。
【能力拓展】
13.3 14.C 15.(1)①30,1;②60,1.5; (2)当∠α=900时,四边形EDBC是菱形. ∵∠α=∠ACB=900,∴BC//ED. ∵CE//AB, ∴四边形EDBC是平行四边形 在Rt△ABC中,∠ACB=900,∠B=600,BC=2,∴∠A=300.∴AB=4,AC=2.∴AO== 在Rt△AOD中,∠A=300,∴AD=2.∴BD=2.∴BD=BC.又∵四边形EDBC是平行四边形,∴四边形EDBC是菱形
16. 22.(1),,.(2)证明:∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,,.
∴△ADE∽△EFC.∴.∵,
∴.
∴.而, ∴
(3)解:过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形.
∴,,.∵四边形DEFG为平行四边形,
∴. ∴.∴. ∴△DBE≌△GHF.
∴△GHC的面积为.由(2)得,□DBHG的面积为.
∴△ABC的面积为.
A
B
O
C
x
y
P
A
B
C
D
E
M
N
D
A
B
C
(图1)
D
A
B
C
D
A
B
C
D
A
B
C
(图4)
(图3)
(图2)
拼法二
拼法一
备用图二
备用图一
图1
图2
图3
(第23题)
图4
(第22题)
y
O
图2
Q(5, 5)
P(2, 3)
y
O
图1
1
1
x
x
A
B
C
例8
D
P
E
时间
距离
O
(B)
时间
距离
O
A
B
D
(第1题)
C
(A)
时间
距离
O
(D)
时间
距离
O
(C)
y
O
x
(第2题)
y
x
O
B
A
(第3题)
或
或
(第7题)
(第5题)
(第6题)
P
第8题图
①
②
③
A
C
D
B
(第13题)
第14题
E
A
B
C
D
F
P
B
C
D
F
E
图1
A
3
6
2
B
C
D
G
F
E
图2
A
D
A
B
C
答案不唯一
D
A
B
C
周长为22
D
A
B
C
周长为26
y
O
1
1
x
A
B
C
B
C
D
G
F
E
图2
A
H
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
直线型几何综合题
一、学习指引
1.知识要点:
三角形及四边形的基本性质,特殊三角形、特殊四边形、全等三角形的判定和性质,轴对称、平移、旋转、相似等变换的性质,一次函数图象和性质。
2.方法指导:
(1)解决动态几何型问题的策略:化“动”为“静”——利用运动中特殊点的位置将图形分类;“静”中求“动”——针对各类图形,分别解决动态问题。
(2)解决图形分割问题的思维方式是:从具体问题出发→观察猜想→实验操作→形成方案→严密计算与论证;图形分割问题的解题策略:比较原图形与分割后图形在边、角、面积等方面的变化是解决图形分割问题的着手点;
(3)新概念性几何题解题策略:正确理解问题中的“新概念”,然后抓住 “新概念”的特征,结合相关的数学知识综合解决问题。
2、 典型例题
例1.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程看作时间的函数,其图像可能是( )
(A) (B) (C) (D)
例2.16.如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),
A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已
知点D在第一象限,且是两直线y1=2x+6、y2=2x-6中某
条上的一点,若△APD是等腰Rt△,则点D的坐标为
例3.如图,点C是线段AB上的一个动点,△ACD和△BCE是在AB同侧的两个等边三角形,DM,EN分别是△ACD和△BCE的高,点C在线段AB上沿着从点A向点B的方向移动(不与点A,B重合),连接DE,得到四边形DMNE.这个四边形的面积变化情况为( )
(A)逐渐增大 (B) 逐渐减小
(C) 始终不变 (D) 先增大后变小
例4.如图1,有一张菱形纸片ABCD,,。
(1) 请沿着AC剪一刀,把它分成两部分,把剪开的两部
分拼成一个平行四边形,在图2中用实数画出你所拼成的平
行四边形;若沿着BD剪开,请在图3中用实线画出拼成的
平行四边形;并直接写出这两个平行四边形的周长。
(2)沿着一条直线剪开,拼成与上述两种都不全等的平行四边形,请在图4
中用实线画出拼成的平行四边形。
(注:上述所画的平行四边形都不能与原菱形全等)
周长为__________ 周长为__________
例5.如图,两个边长分别为4和3的正方形,请用线段将它们进行适当分割,剪拼成一个大正方形,请在下图中分别画出两种不同的拼法,并将剪拼前、后的相同区域用相同数字序号标出.
例6.如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果,请直接写出∠CDF的度数和的值.
例7.类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+()=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量” {1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量” {3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
例8.如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连结PC, 过点P作PE⊥PC交AB于E
(1)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求线段AP与AQ之间的数量关系;若不存在,请说明理由;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,求BE的取值范围.
直线型几何综合题同步练习
【基础巩固】
1.如图,一艘旅游船从A点驶向C点. 旅游船先从A点沿以D为圆心的弧AB行驶到B点,然后从B点沿直径行驶到圆D上的C点.假如旅游船在整个行驶过程中保持匀速,则下面各图中,能反映旅游船与D点的距离随时间变化的图象大致是( )
2.如图,A,B的坐标为(2,0),(0,1)若将线段平移至,则—2()的值为( )
A.2 B.3 C.4 D.5
3.如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 ( )
(A)(0,0) (B)(,)
(C)(-,-) (D)(-,-)
4.如图,一个的矩形可以用3种不同的方式分割成2或5或8个小正方形,那么一个的矩形用不同的方式分割后,小正方形的个数可以是
5.如图,在平面直角坐标系中,为原点,四边形是矩形,A(10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是 。
6.如图,将边长为1的正三角形沿轴正方向连续翻转2008次,点依次落在点的位置,则点的横坐标为 .
7.矩形ABCD的边AB=8,AD=6,现将矩形ABCD放在直线l上且沿着l向右作无滑动地翻滚,当它翻滚至类似开始的位置时(如图所示),则顶点A所经过的路线长是_________ .
8.如图,正方形ABCD边长为1,动点P从A点出发,沿正方形的边按逆时针方向运动,当它的运动路程为2009时,点P所在位置为______;当点P所在位置为D点时,点P的运动路程为______(用含自然数n的式子表示).
9.如图,矩形ABCD中,AB=8,BC=6,画出面积不相等的三个菱形,使菱形的顶点都在矩形的边上,并分别求出所画菱形的面积。(下列图形供画图用)
10.(1)请在图①的正方形ABCD内,画出使∠APB=90°的一个点P,并说明理由.
(2)请在图②的正方形ABCD内(含边),画出使∠APB=60°的所有的点P,并说明理由。
(3)如图③,现在一块矩形钢板ABCD,AB=4,BC=3,工人师傅想用它裁出两块全等的、面积最大的△APB和△CPD钢板,且∠APB=∠CPD=60°,请你在图③中画出符合要求的点P和P.
11.如图,四边形ABCD中,AB=AD,CB=CD,但ADCD,我们称这样的四边形为“半菱形”。小明说“‘半菱形’的面积等于两条对角线乘积的一半”。他的说法正确吗?请你判断并证明你的结论.
12.如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5,BC=12,CD=,∠C=45°,点P是BC边上一动点,设PB的长为x.
(1)当x的值为____________时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为____________时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
【能力拓展】
13.如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________.
14.如图,一种电子游戏,电子屏幕上有一正六边形ABCDEF,点P沿直线AB从右向左移动,当出现点P与正六边形六个顶点中的至少两个顶点距离相等时,就会发出警报,则直线AB上会发出警报的点P有( )
A.3个 B.4个 C.5个 D.6个
15.如图,在Rt△ABC中,∠ACB=90°, ∠B =60°,BC=2.点0是AC的中点,过点0的直线l从与AC重合的位置开始,绕点0作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.
(1)①当α=________度时,四边形EDBC是等腰梯形,此时AD的长为_________;
②当α=________度时,四边形EDBC是直角梯形,此时AD的长为_________.
(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.
16. 问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,
过点E作EF∥AB交BC于点F.请按图示数据填空:
四边形DBFE的面积 ,
△EFC的面积 ,
△ADE的面积 .
探究发现
(2)在(1)中,若,,DE与BC间的距离为.请证明.
拓展迁移
(3)如图2,□DEFG的四个顶点在△ABC的三边上,若
△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)
中的结论求△ABC的面积.
例题与同步练习参考答案
直线型几何综合题(典型例题)
例1. A例2. (4,2),(4,14),(,),(,) 例3.C
例4.
例5.
例6.(1)① = ② >
(2)>
证明:作点C关于FD的对称点G,
连接GK,GM,GD,
则CD=GD ,GK = CK,∠GDK=∠CDK,
∵D是AB的中点,∴AD=CD=GD.
∵30°,∴∠CDA=120°,∵∠EDF=60°,∴∠GDM+∠GDK=60°,∠ADM+∠CDK =60°.∴∠ADM=∠GDM,∵DM=DM,∴△ADM≌△GDM,∴GM=AM.∵GM+GK>MK,∴AM+CK>MK.(3)∠CDF=15°,.
例7.(1){3,1}+{1,2}={4,3}. {1,2}+{3,1}={4,3}.
(2)①画图 最后的位置仍是B.
② 证明:由①知,A(3,1),B(4,3),C(1,2)
∴OC=AB==,OA=BC==,
∴四边形OABC是平行四边形.(3){2,3}+{3,2}+{-5,-5}={0, 0}.
例8. (1)当P是AD的中点时,满足条件的点Q不存在;当P不是AD的中点时,总存在这样的点Q满足条件,此时AP+AQ=3 (2) 7/8≦BE<2
直线型几何综合题(同步练习)
【基础巩固】
1.B; 2.D ;3.C ; 4.4或7或9或12或15个小正方形; 5.(4,3)(1,3)(9,3);6. 2008; 7.12π;8.点B;4n+3;
9.
10. (1)如图①,点P为所求(2)如图②,圆上实线部分弧EF为所求②③
(3)如图③,点、为所求
11.
12.(1)3或8 (2)1或11 (3)能构成菱形。
【能力拓展】
13.3 14.C 15.(1)①30,1;②60,1.5; (2)当∠α=900时,四边形EDBC是菱形. ∵∠α=∠ACB=900,∴BC//ED. ∵CE//AB, ∴四边形EDBC是平行四边形 在Rt△ABC中,∠ACB=900,∠B=600,BC=2,∴∠A=300.∴AB=4,AC=2.∴AO== 在Rt△AOD中,∠A=300,∴AD=2.∴BD=2.∴BD=BC.又∵四边形EDBC是平行四边形,∴四边形EDBC是菱形
16. 22.(1),,.(2)证明:∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,,.
∴△ADE∽△EFC.∴.∵,
∴.
∴.而, ∴
(3)解:过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形.
∴,,.∵四边形DEFG为平行四边形,
∴. ∴.∴. ∴△DBE≌△GHF.
∴△GHC的面积为.由(2)得,□DBHG的面积为.
∴△ABC的面积为.
A
B
O
C
x
y
P
A
B
C
D
E
M
N
D
A
B
C
(图1)
D
A
B
C
D
A
B
C
D
A
B
C
(图4)
(图3)
(图2)
拼法二
拼法一
备用图二
备用图一
图1
图2
图3
(第23题)
图4
(第22题)
y
O
图2
Q(5, 5)
P(2, 3)
y
O
图1
1
1
x
x
A
B
C
例8
D
P
E
时间
距离
O
(B)
时间
距离
O
A
B
D
(第1题)
C
(A)
时间
距离
O
(D)
时间
距离
O
(C)
y
O
x
(第2题)
y
x
O
B
A
(第3题)
或
或
(第7题)
(第5题)
(第6题)
P
第8题图
①
②
③
A
C
D
B
(第13题)
第14题
E
A
B
C
D
F
P
B
C
D
F
E
图1
A
3
6
2
B
C
D
G
F
E
图2
A
D
A
B
C
答案不唯一
D
A
B
C
周长为22
D
A
B
C
周长为26
y
O
1
1
x
A
B
C
B
C
D
G
F
E
图2
A
H
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
