二次函数

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
二次函数
一、学习指引
1.知识要点
（1）形如y=ax2+bx+c(a,b,c是常数，a≠0)的函数，叫二次函数．
（2） 二次函数的图像.
一般地，平移二次函数y=ax2的图象便可得到二次函数y=a（x- h）2+k的图象．
（3）图象的性质.
1.二次函数y= ax2+bx+c = a（x＋）2＋的图象是以x =－为对称轴，以（－，）为顶点的抛物线．
2.二次函数y=ax2+bx+c的图象，如图2，当a > 0时，其图象的开口向上，这时当x <－ 时y的值随x的增大而减小；当x >－时y的值随x的增大而增大；当x =－时，y有最小值．如图3，当a < 0时，其图象的开口向下，这时当x <－时y的值随x的增大而增大；当x >－时y的值随x的增大而减小；当x =－时，y有最大值．
3.二次函数y=ax2+bx+c的图象的二次项系数a——定形,│a│的大小决定了开口的宽窄，│a│越大，开口越小；a ，b的符号共同决定了对称轴的位置，当b=0时，对称轴x=0，即对称轴为y轴；c的符号决定了抛物线与y轴交点的位置，c=0时，抛物线经过原点.
2.方法指引
（1）结合函数图象类比学习本讲内容 ．
（2）掌握一般式y=ax2+bx+c、顶点式y=a(x-h)2+k、交点式y=a(x-x1)(x-x2)之间的互化．用待定系数发求解析式．
（3）能数形结合进行一些简单的函数应用.
二、典型例题
例1. （山东德州2010）某游泳池的横截面如图，用一水管向池内持续注水，若单位时间内注入的水量保持不变，则在注水过程中，下列图象能反映深水区水深h与注水时间t关系的是（ ）
A . B. C . D.
例２．在下列函数关系式中，哪些是二次函数（是二次函数的在括号内打上“√”，不是的打“x”).
(l）y=-2x2 ( ) (2）y=x-x2 ( )
(3）y=2(x-1)2+3 ( ) (4）s=a(8-a) ( )
例３．描点法画二次函数y=x2与y=-x2的图象，并简述其性质.
例4．画出并说明二次函数y=x2 与y=x2 +1、y=x2-2的图象及其平移关系.
例5．（荆州市２０１０）若把函数y=x的图象用E（x，x）记，函数y=2x+1的图象用E（x，2x+1）记，……则E（x，）可以由E（x，）怎样平移得到？
A．向上平移１个单位 　B．向下平移１个单位
C．向左平移１个单位 D．向右平移１个单位
例6．说明二次函数y=x2 与y=（x-1）2 +2的图象平移关系，及y=（x-1）2 +2的对称轴、顶点坐标、最值、增减性.
例7．（1）说明抛物线y=2x2-5x+4的开口方向、对称轴、顶点坐标、最值、增减性.
（2）ｙ＝４ｘ２－８ｘ＋３呢？ y=ax2+bx+c呢？
例8．根据下列条件求关于x的二次函数的解析式：
（1） 当x=1时，y=0;x=0时,y= -2，x=2 时，y=3；
（2） 抛物线顶点坐标为（-1，-2）且通过点（1，10）；
（3） 当x=3时，y最小值=-1，且图象过（0，7）；
（4） 图象经过（0，1）（1，0）（3，0）.
例9．二次函数的图象如图所示，则，
，，这四个式子中，值为
正数的有（ ）．
A．4个 B． 3个 C． 2个 D． 1个
例10．（2009年台州市）
已知二次函数的与的部分对应值如下表：
… 0 1 3 …
… 1 3 1 …
则下列判断中正确的是（　 　）
A．抛物线开口向上　　　　　　 B．抛物线与轴交于负半轴
C．当＝4时，＞0 D．方程的正根在3与4之间
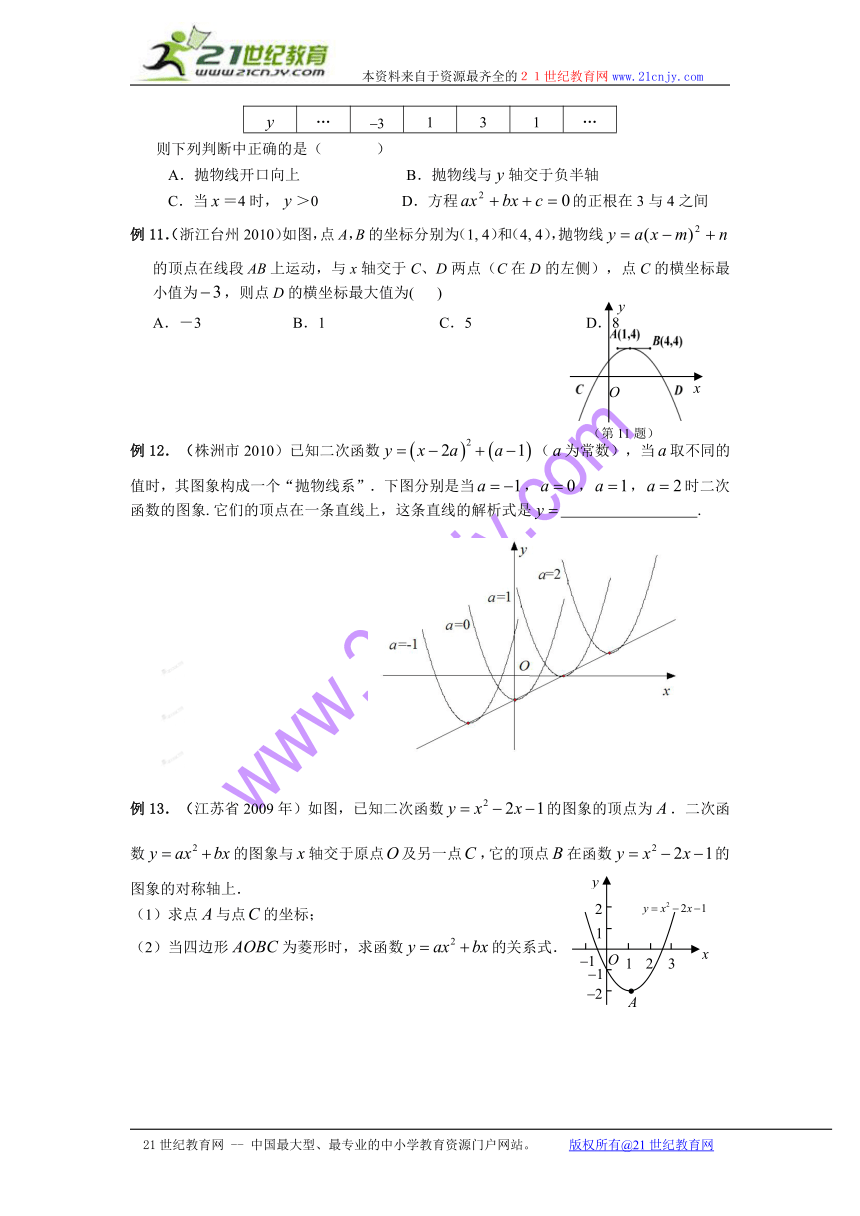
例11．（浙江台州2010）如图，点A，B的坐标分别为（1, 4）和（4, 4），抛物线的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为，则点D的横坐标最大值为( )
A．－3 　 B．1 C．5 D．8
例12．（株洲市2010）已知二次函数（为常数），当取不同的值时，其图象构成一个“抛物线系”．下图分别是当，，，时二次函数的图象.它们的顶点在一条直线上，这条直线的解析式是 .



例13．（江苏省2009年）如图，已知二次函数的图象的顶点为．二次函数的图象与轴交于原点及另一点，它的顶点在函数的图象的对称轴上．
（1）求点与点的坐标；
（2）当四边形为菱形时，求函数的关系式．
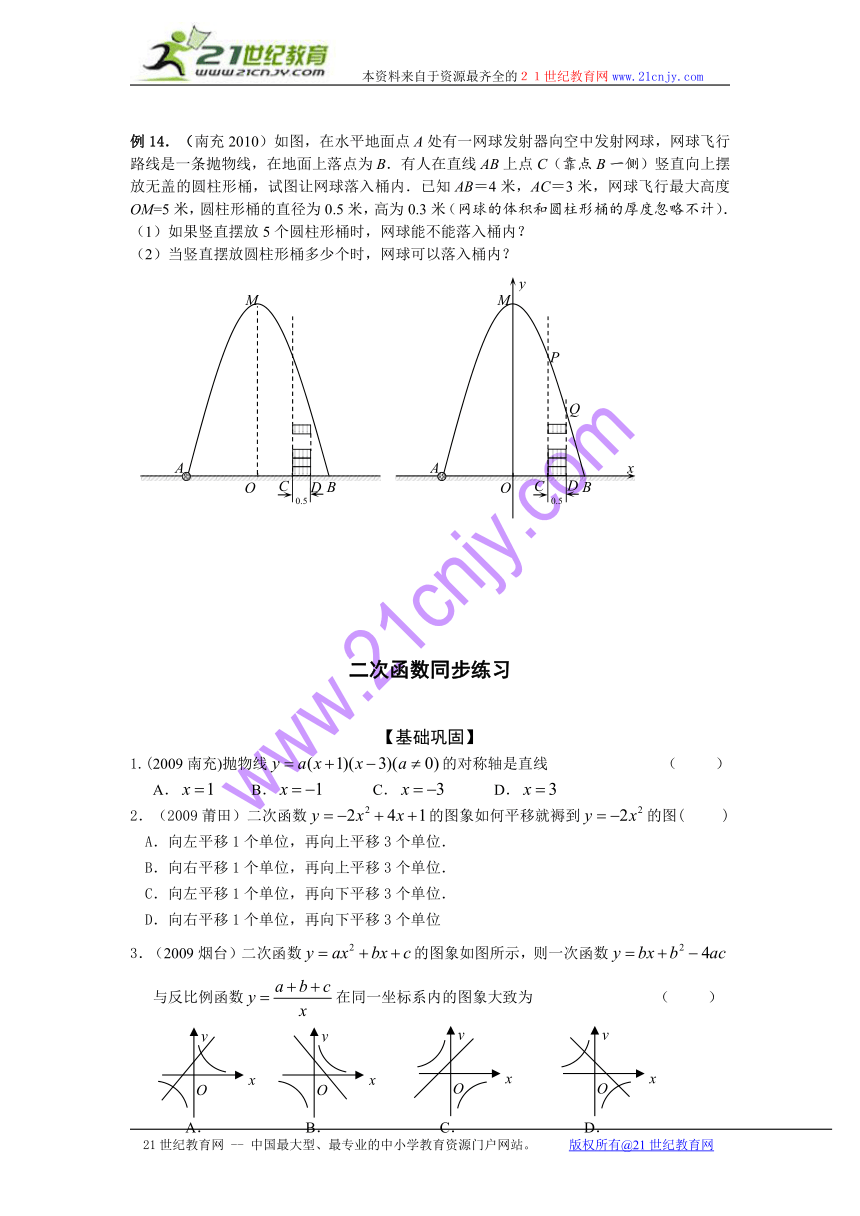
例14．（南充2010）如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB＝4米，AC＝3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．
（1）如果竖直摆放5个圆柱形桶时，网球能不能落入桶内？
（2）当竖直摆放圆柱形桶多少个时，网球可以落入桶内？
　
二次函数同步练习
【基础巩固】
1.(2009南充)抛物线的对称轴是直线 （ ）
A． B． C． D．
2．（2009莆田）二次函数的图象如何平移就褥到的图( )
A．向左平移1个单位，再向上平移3个单位．
B．向右平移1个单位，再向上平移3个单位．
C．向左平移1个单位，再向下平移3个单位．
D．向右平移1个单位，再向下平移3个单位
3．（2009烟台）二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为 （ ）
4．（2010年河北省）如图，已知抛物线的对称轴为，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为（0，3），则点B的坐标为（ ）
A．（2，3） B．（3，2）
C．（3，3） D．（4，3）
5．（2009丽水）已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，给出以下结论：①a＞0. ②该函数的图象关于直线对称.
③当时，函数y的值都等于0. 其中正确结论的个数是（ ）
A．3 B．2 C．1 D．0
6．（2010广安）已知二次函数的图象如
右图所示，下列结论：① ② ③
④的实数)， 其中正确的结论有（ ）
A．1个 B．2个 C．3个 D．4个
7．（2008年陕西）已知二次函数（其中a＞0， b＞0，c＜0），
关于这个二次函数的图象有如下说法：
①图象的开口一定向上；②图象的顶点一定在第四象限；
③图象与x轴的交点至少有一个在y轴的右侧.
以上说法正确的个数为 （ ）
A．0 B．1 C．2 D．3
8．抛物线与y轴的交点坐标是 ， 与x轴的交点坐标是 .
9．（2009南州）二次函数的图象关于原点O
（0, 0）对称的图象的解析式是_________________.21世纪教育网
10．（2009湖州）已知抛物线（＞0）的对称轴为直线，且经过点，试比较和的大小： _（填“>”，“<”或“=”）
11．（兰州市2010）如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为 米.
12．(吉林通化2010)已知抛物线y＝ax2＋bx＋c的部分图象如图所示，若y＞0，则x的取值范围是 ．
13．（2010浙江金华）已知二次函数y=ax2＋bx－3的图象经过点A（2，－3），
B（－1，0）．
（1）求二次函数的解析式；
（2）填空：要使该二次函数的图象与x轴只有一个交点，应把图象沿y轴向上平移
个单位．
【能力拓展】
14．函数，．当时，x的范围是
（ ）
A.．x＜－1 　　B．－1＜x＜2
C．x＜－1或x＞2 D．x＞2
15．（上海2010）如图8，已知平面直角坐标系xOy，抛物线y＝－x2＋bx＋c过点A(4,0)、B(1,3) .
（1）求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；
（2）记该抛物线的对称轴为直线l，设抛物线上的点P(m,n)在第四象限，点P关于直线l的对称点为E，点E关于y轴的对称点为F，若四边形OAPF的面积为20，求m、n的值.
16．（浙江温州2010）如图，抛物线y=ax2+bx经过点A(4，0)，B(2，2)。连结OB，AB．
(1)求该抛物线的解析式；
(2)求证：△OAB是等腰直角三角形；
(3)将△OAB绕点0按顺时针方向旋转l35°得到△0A′B′，写出△0A′B′斜边A′B中点
P的坐标．试判断点P是否在此抛物线上，并说明理由．
17．（湖北省荆门市2009年）一开口向上的抛物线与x轴交于A（，0），
B（m＋2，0）两点，记抛物线顶点为C，且AC⊥BC．
（1）若m为常数，求抛物线的解析式；
（2）若m为小于0的常数，那么（1）中的抛物线经过怎么样的平移可以使顶点在坐标原点？
（3）设抛物线交y轴正半轴于D点，问是否存在实数m，使得△BCD为等腰三角形？若存在，求出m的值；若不存在，请说明理由．
18．（2009年深圳市）如图，在直角坐标系中，点A的坐标为（－2，0），连结OA，将线段OA绕原点O顺时针旋转120°，得到线段OB.
（1）求点B的坐标；
（2）求经过A、O、B三点的抛物线的解析式；
（3）在（2）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由.
（4）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由.
例题与同步练习参考答案
第八讲 二次函数 （典型例题）
例1．A
例２．√ 　√ 　√ √
例３． 见课件　　
例4．见课件
例５．D
例６． 略
例７． 略
例８．（１）．　（2） 　　
（３）　　 （４）．　　
例９． 　B
例１０． D
例１１ D
例１２．
例１３
例１４．解：（1）以点O为原点，AB所在直线为x轴建立直角坐标系（如图）．　
M（0，5），B（2，0），C（1，0），D（，0）
设抛物线的解析式为，
抛物线过点M和点B，则　，．
即抛物线解析式为．　　　　　　　　　　　　　　　　
当x＝时，y＝；当x＝时，y＝．
即P（1，），Q（，）在抛物线上．
当竖直摆放5个圆柱形桶时，桶高＝×5＝．
∵　＜且＜，∴网球不能落入桶内．　　　　　　　　　　　
（2）设竖直摆放圆柱形桶m个时网球可以落入桶内，
　　由题意，得，≤m≤．　　　　　　　　　　　　　　　　
　　　　　解得，≤m≤．
∵　m为整数，∴　m的值为8，9，10，11，12．　　　　　
∴　当竖直摆放圆柱形桶8，9，10，11或12个时，网球可以落入桶内
第八讲 二次函数 （同步练习）
【基础巩固】
1．A 2．C 3．D 4．D 5．B 6．C 7．C
8．（0，-4） （-4，0） （1，0） 9．
10．＞ 11． 12．-1＜ x ＜ 3
13．解：（1解：(1)由已知，有，即，解得
∴所求的二次函数的解析式为.
(2)4
【能力拓展】
14．C
15．解 （1）解：将A(4,0)、B(1,3)两点坐标代入抛物线的方程得：
解之得：b=4，c=0
所以抛物线的表达式为：
将抛物线的表达式配方得：
所以对称轴为x=2，顶点坐标为（2，4）
（2）点p（m，n）关于直线x=2的对称点坐标为点E（4－m，n），则点E关于y轴对称点为点F坐标为（4－m,－n），
则四边形OAPF可以分为：三角形OFA与三角形OAP，则
= + = =20
所以=5，因为点P为第四象限的点，所以n<0，所以n= －5
代入抛物线方程得m=5
16．
17．解：（1）设抛物线的解析式为： y＝a（x－m＋2）（x－m－2）＝a（x－m）2－4a．
∵AC⊥BC，由抛物线的对称性可知：△ACB为等腰直角三角形，又AB＝4，
∴C（m，）代入得a＝．∴解析式为：y＝（x－m）2．
（亦可求C点，设顶点式）
（2）∵m为小于零的常数，∴只需将抛物线向右平移－m个单位，再向上平移2个单位，可以使抛物线y＝（x－m）2顶点在坐标原点．
（3）由（1）得D（0，m2），设存在实数m，使得△BOD为等腰三角形．
∵△BOD为直角三角形，∴只能OD＝OB．
∴m2－2＝|m＋2|，当m＋2＞0时，解得m＝4或m＝（舍）．
当m＋2＜0时，解得m＝0（舍）或m＝（舍）；
当m＋2＝0时，即m＝时，B．O．D三点重合（不合题意，舍）
综上所述：存在实数m＝4，使得△BOD为等腰三角形．
18．解：（1）B（1，）
（2）设抛物线的解析式为y=ax(x+a)，代入点B（1, ），得，
因此
（3）如图，抛物线的对称轴是直线x=—1，当点C位于对称轴与线段AB的交点时，△BOC的周长最小.
设直线AB为y=kx+b.所以，
因此直线AB为，
当x=－1时，，
因此点C的坐标为（－1，）.
（4）如图，过P作y轴的平行线交AB于D.
当x=－时，△PAB的面积的最大值为，此时.
y=ax2
上、下移
y=ax2+k
左、右移
y=a（x- h）2
y=a（x- h）2+k
左、右移
上、下移
上、下移且左、右移
x=－
y
x
O
x=－
x
y
O
图2
图3
第1题图
深
水
区
浅水区
t
h
O
t
h
O
t
h
O
h
t
O
例9
y
x
O
（第11题）
x
y
O
1
2
3
2
1
A
A
M
B
C
0.5
O
D
A
M
B
C
0.5
O
x
y
D
P
Q
y
x
O
y
x
O
B．
C．
y
x
O
A．
y
x
O
D．
O
x
y
A
图4
x = 2
B
(第5题)
y
x
-1
1
3
第12题图
图15
O
B
A
C
D
x
y
B
A
O
y
x
A
M
B
C
0.5
O
x
y
D
P
Q
图8
C
B
A
O
y
x
D
B
A
O
y
x
P
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网