数学思想与方法专题复习
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
数学思想方法
一、学习指引
1.知识要点:
数形结合思想;分类讨论思想;转化化归思想;方程与函数思想
2.方法指引:
(1)数形结合法:每个几何图形中蕴含着一定的数量关系,而数量关系常常又通过图形的直观性作出反映和描述,数与形之间可以相互转化,将问题化难为易,化抽象为具体. 数形结合的思想方法通过借数解形、以形助数,能使某些较复杂的数学问题迎刃而解.
(2)分类讨论法:在数学中,我们常常需要根据研究对象性质的差异,分各种不同情况
予以考查.这种分类思考的方法是一种重要的数学思想方法,同时也是一种解题策略.分
类是按照数学对象的相同点和差异点,将数学对象区分为不同种类的思想方法,掌握分类
的方法,领会其实质,对于加深基础知识的理解.提高分析问题、解决问题的能力是十分
重要的.正确的分类必须是周全的,既不重复、也不遗漏.
分类的原则:(1)分类中的每一部分是相互独立的;(2)一次分类按一个标准;(3)分
讨论应逐级进行.
(3)转化化归思想:所谓化归思想就是化未知为已知、化繁为简、化难为易.如将分式
方程化为整式方程,将代数问题化为几何问题,将四边形问题转化为三角形问题等.实现
这种转化的方法有:待定系数法、配方法、整体代人法以及化动为静、由抽象到具体等.
(4)方程与函数思想:方程与函数是研究数量关系的重要工具,在处理某些问题时,往
往根据已知与未知之间的内在联系和相等关系建立方程(或方程组)或函数关系,这种通
过方程(组)或函数来沟通已知与未知,从而使问题获得解决的思想方法称之为方程与函
数思想.
二、典型例题
例1.(2009丽水)甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1) 他们在进行 ▲ 米的长跑训练,在0<x<15的时
段内,速度较快的人是 ▲ ;
(2) 求甲距终点的路程y(米)和跑步时间 x(分)之间的函数关系式;
(3) 当x=15时,两人相距多少米?在15<x<20的时段内,求两人速度之差.
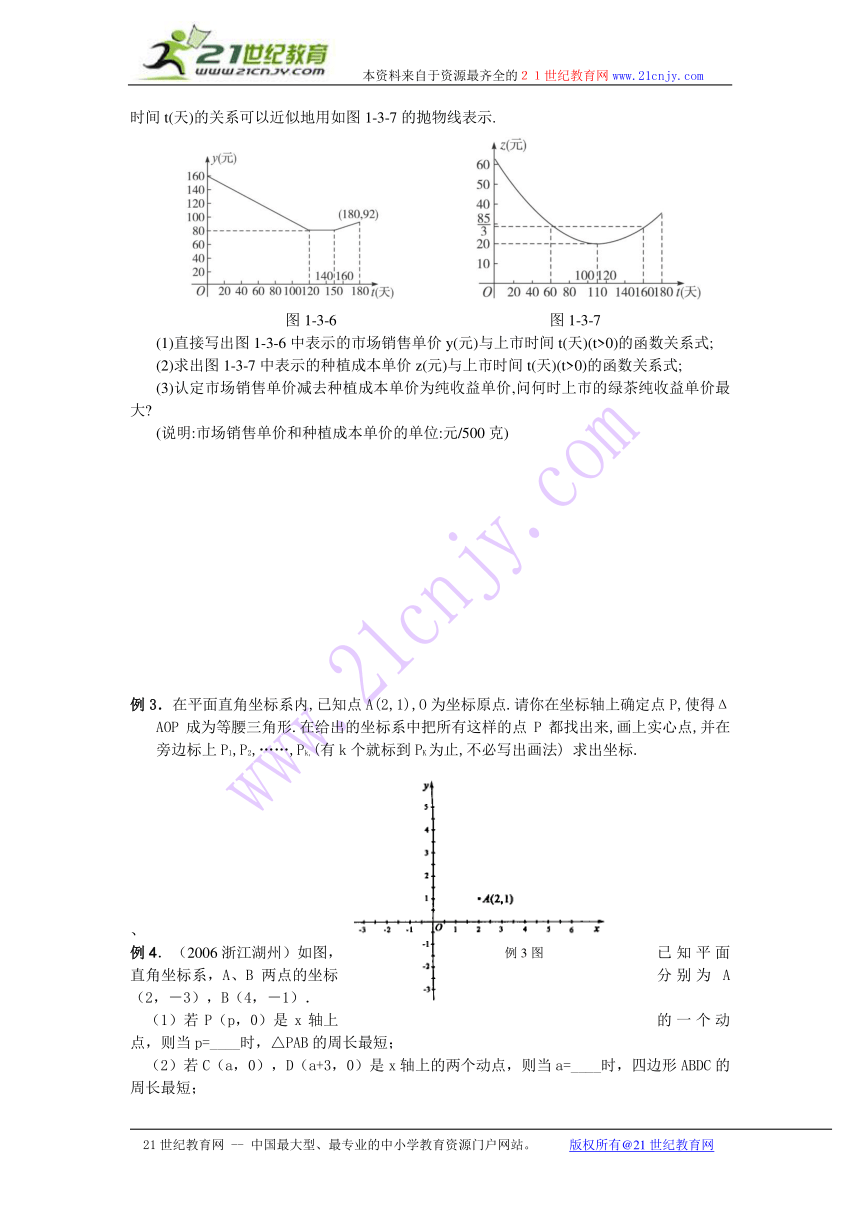
例2.我市英山县某茶厂种植 “春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价y(元)与上市时间t(天)的关系可以近似地用如图1-3-6中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z(元)与上市时间t(天)的关系可以近似地用如图1-3-7的抛物线表示.
图1-3-6 图1-3-7
(1)直接写出图1-3-6中表示的市场销售单价y(元)与上市时间t(天)(t>0)的函数关系式;
(2)求出图1-3-7中表示的种植成本单价z(元)与上市时间t(天)(t>0)的函数关系式;
(3)认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大
(说明:市场销售单价和种植成本单价的单位:元/500克)
例3.在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得ΔAOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,……,Pk,(有k个就标到PK为止,不必写出画法) 求出坐标.
、
例4.(2006浙江湖州)如图,已知平面直角坐标系,A、B两点的坐标分别为A(2,-3),B(4,-1).
(1)若P(p,0)是x轴上的一个动点,则当p=____时,△PAB的周长最短;
(2)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=____时,四边形ABDC的周长最短;
(3)设M,N分别为x轴和y轴上的动点,请问:是否存在这样的点M(m,0)、N(0,n),使四边形ABMN的周长最短?若存在,请求出m=____,n=___(不必写解答过程);若不存在,请说明理由.
例5.(2009丽水)绿谷商场“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示:
类别 冰箱 彩电
进价(元/台) 2 320 1 900
售价(元/台) 2 420 1 980
(1) 按国家政策,农民购买“家电下乡”产品可享受售价13%的政府补贴.农民田大伯到该商场购买了冰箱、彩电各一台,可以享受多少元的政府补贴?
(2)为满足农民需求,商场决定用不超过85 000元采购冰箱、彩电共40台, 且冰箱的数量不少于彩电数量的.
①请你帮助该商场设计相应的进货方案;
②哪种进货方案商场获得利润最大(利润=售价进价),最大利润是多少?
例6.(2006湖南常德中考)把两块全等的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1-3-12(1),当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时AP·CQ=_________________.
(2)将三角板DEF由图1-3-12(1)所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP·CQ的值是否改变 说明你的理由.
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图1-3-12中(2)(3)供解题用).
数学思想方法同步练习
【基础巩固】
1.不等式组的解集在数轴上,如图表示应是 ( )
2.若等腰三角形的一个内角为50则其他两个内角为 ( )
A.500 ,80o B.650, 650
C.500 ,650 D.500,800或 650,650
3.一次函数y=kx+b的图象经过点A(0,-2)和B(-3,6)两点,那么该函数的表达式是 ( )
4.设一个三角形的三边长为3,l-2m,8,则m的取值范围是 ( )
A.0<m< B. -5<m- 2 C.-2<m <5 D.-<m<-l
5.如果表示a、b为两个实数的点在数轴上的位置如图3-l-8所示,那么化简的结果等于 ( )
A.2a B.2b C.-2a D.-2b
6.如图3-3-8所示,阴影部分是一个正方形,则此正方形的面积为 ( )
A.8 B.64 C.16 D.32
7.某村办工厂今年前5个月生产某种产品的总量 (件)关于时间t(月)的图象如图3-3-9所示,则该厂对这种产品来说 ( )
A.1月至3月每月生产总量逐月增加,4、5两月生产总量逐月减少;
B.1月至3月每月生产总量逐月增加,4、5两月生产总量与3月持平;
C.1月至3月每月生产总量逐月增加,4、5两月均停止生产;
D.1月至 3月每月生产总量不变,4、5两月均停止生产.
8.若
A.5或-1 B.-5或1; C.5或1 D.-5或-1
9.若解方程产生增根,则m的值是( )
A.-1或-2 B.-1或2 C.1或2 D.1或-2
10.水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如图甲所示,出水口出水量与时间的关系如图乙所示.某天0点到6点,该水池的蓄水量与时间的关系如图丙所示.
下列论断:①0点到1点,打开两个进水口,关闭出水口;②1点到3点,同时关闭两个进水口和-个出水口;③3点到4点,关门两个进水口,打开出水口;④5点到6点.同时打开两个进水口和一个出水口.其中,可能正确的论断是 ( )
A. ①③ B. ①④ C. ②③ D.②④
11.若一次函数的图象经过第一、二、四象限时,m的取值范围是_______.
12.已知直线y1=2x-1和y2=-x-1的图象如图3-3-24所示,根据图象填空.
⑴ 当x______时,y1>y2;当x______时,y1=y2;当x______时,y1<y2.
⑵ 方程组的解是_____________.
13. 已知二次函数与一次函数 y2=kx+ m(k≠0)的图象相交于点 A(-2,4),B(8,2)(如图 3-3-25所示),则能使y1>y2成立的x的取值范围是________.
14.已知直角三角形的两条边长分别和,则斜边上的高为 (结果保留根号).
15.将自然数按以下规律排列,则2008所在的位置是第 行第 列.
16.如图 3-1-2,梯形 ABCD中,AD∥BC,AB=CD,对角线AC、BD相交于O点,且AC⊥BD,AD=3,BC=5,求AC的长.
17.某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,图3-3-1已表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:
(1)求y1与y2的函数解析式;
(2)解释图中表示的两种方案是如何付推销费的?
(3)果你是推销员,应如何选择付费方案?
18.如图3-1-1,反比例函数y=-与一次函数y=-x+2的图象交于A、B两点.
(1)求 A、B两点的坐标;
(2)求△AOB的面积.
【能力拓展】
19.如图,已知直角坐标系内的梯形AOBC(O为原点),AC∥OB,OC⊥BC,AC,OB的长是关于x的方程x2-(k+2)x+5=0的两个根,且S△AOC:S△BOC=1:5.
(1)填空:0C=________,k=________;
(2)求经过O,C,B三点的抛物线的另一个交点为D,动点P,Q分别从O,D同时出发,都以每秒1个单位的速度运动,其中点P沿OB由O→B运动,点Q沿DC由D→C运动,过点Q作QM⊥CD交BC于点M,连结PM,设动点运动时间为t秒,请你探索:当t为何值时,△PMB是直角三角形.
第19题图
20.在四边形ABCD中,对角线AC平分∠DAB.如图(1),当∠DAB=120°,∠B=∠D=90°时,易证:AB+AD=AC.
(1) 如图(2),当∠DAB=120°,∠B与∠D互补时,线段AB、AD、AC有怎样的数量关系?写出你的猜想,并给予证明;
(2) 如图(3),当∠DAB=90°,∠B与∠D互补时,线段AB、AD、AC又有怎样的数量关系?写出你的猜想,不需证明.
第20题图
例题与同步练习参考答案
第九讲 数学思想方法(典型例题)
例1.解:(1)5000 甲
(2)设所求直线的解析式为:
y =kx+b(0≤x≤20),
由图象可知:b=5000,当x=20时,y=0,
∴0=20k+5000,解得k= -250.
即y = -250x+5000 (0≤x≤20)
(3)当x=15时,y = -250x+5000= -250×15+5000=5000-3750=1250.
两人相距:(5000 -1250)-(5000-2000)=750(米).
两人速度之差:750÷(20-15)=150(米/分)
例2.解:(1)依题意,可建立的函数关系式为
y=
(2)由题目已知条件可设z=a(t-110)2+20.
∵图象过点(60,),
∴=a(60-110)2+20.∴a=.
∴z=(t-110)2+20(t>0).
(3)设纯收益单价为W元,则W=销售单价-成本单价.
故W=
化简得W=
①当W=- (t-10)2+100(0②当W=- (t-110)2+60(120≤t<150)时,由图象知有t=120时,W最大,最大值为;
③当W=-(t-170)2+56(150≤t≤180)时,有t=170时,W最大,最大值为56.
综上所述,在t=10时,纯收益单价有最大值,最大值为100元.
例3.解:以A为圆心,OA为半径作圆交坐标轴得和;以O为圆心,OA为半径作圆交坐标轴得 ,,和;作OA的垂直平分线交坐标轴得和
例4.解:(1) (2)
(3)存在使四边形ABMN周长最短的点M.N,m=,n= HYPERLINK "http://" EMBED Equation.DSMT4 .
例5.解:(1) (2 420+1 980)×13%=572
答: 可以享受政府572元的补贴.
(2) ①设冰箱采购x台,则彩电采购(40-x)台,根据题意,得
2 320x+1 900(40-x)≤85 000,
x≥(40-x).
解不等式组,得≤x≤
∵x为正整数.
∴x= 19,20,21.
∴该商场共有3种进货方案:
方案一:冰箱购买19台,彩电购买21台
方案二:冰箱购买20台,彩电购买20台;
方案三:冰箱购买21台,彩电购买19台.
②设商场获得总利润y元,根据题意,得
y=(2 420 2 320)x+(1 980 40-x)=20x+3 200
∵20>0, ∴y随x的增大而增大
∴当x=21时,y最大=20×21+3 200=3 620
答:方案三商场获得利润最大,最大利润是3 620元
例6.解:(1)8
(2)AP·CQ的值不会改变,
理由如下: 如右图,在△APD与△CDQ中,∠A=∠C=45°,
∠APD=180°-45°-(45°+α)=90°-α,
∠CDQ=90°-α,即∠APD=∠CDQ.
∴△APD∽△CDQ.∴.
∴AP·CQ=AD·CD=AD2=(AC)2=8.
(3)如图,情形一:当0°<α<45°时,2由(2)知AP·CQ=8得AP=.
于是y=AB·AC-CQ·DN-AP·DG=8-x-(2情形二:当45°≤α<90°时,0由于AP=,PB=-4,易证:△PBM∽△DNM,
∴.
解得BM=.
∴MQ=4-BM-CQ=4-x-.
于是y=MQ·DN=4-x-(0综上所述,当2当0第九讲 数学思想方法(同步练习)
【基础巩固】
1—10 ADDBD; BCCDD 11.略12.略13.略14. 15.18 45
16. 解:过 D作DE⊥AC交BC的延长线于E,则得AD=CE.AC=DE.所以BE=BC+CE=8.
因为 AC⊥BD,所以BD⊥DE.
因为 AB=CD, 所以AC=BD.所以GD=DE.
在Rt△BDE中,BD2+DE2=BE2
所以BD=BE=4,即AC=4.
17.解:(1)y1=20x,y2=10x+300.
(2)y1是不推销产品没有推销费,每推销10件产品得推销费200元,y2是保底工资300元,每推销 10件产品再提成100元.
(3)若业务能力强,平均每月保证推销多于30件时,就选择y1的付费方案;否则,选择y2的付费方案.
18..解:⑴解方程组 得
所以A.B两点的坐标分别为A(-2,4)B(4,-2
(2)因为直线y=-x+2与y轴交点D坐标是(0, 2),
所以 所以
【能力拓展】
19.(1);(2)略
20. (1)AB+AD=AC证明如下:过C点分别作AD.AB的垂线,垂足分别为E.F。
∵ AC平分∠DAB,∴ CE=CF.∵ ∠D+∠ABC=180°,∠CBF+∠ABC=180°,
∴ ∠D=∠CBF.∵ ∠CED=∠CFB,∴ △CED≌△CFB .∴ ED=BF.∴ AD+AB=AE+ED+AB=AE+AF=AC . (2)AB+AD=AC.
(例1图)
例3图
A
B
C
D
图1
A
B
C
D
图(2)
A
B
C
D
图(3)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
数学思想方法
一、学习指引
1.知识要点:
数形结合思想;分类讨论思想;转化化归思想;方程与函数思想
2.方法指引:
(1)数形结合法:每个几何图形中蕴含着一定的数量关系,而数量关系常常又通过图形的直观性作出反映和描述,数与形之间可以相互转化,将问题化难为易,化抽象为具体. 数形结合的思想方法通过借数解形、以形助数,能使某些较复杂的数学问题迎刃而解.
(2)分类讨论法:在数学中,我们常常需要根据研究对象性质的差异,分各种不同情况
予以考查.这种分类思考的方法是一种重要的数学思想方法,同时也是一种解题策略.分
类是按照数学对象的相同点和差异点,将数学对象区分为不同种类的思想方法,掌握分类
的方法,领会其实质,对于加深基础知识的理解.提高分析问题、解决问题的能力是十分
重要的.正确的分类必须是周全的,既不重复、也不遗漏.
分类的原则:(1)分类中的每一部分是相互独立的;(2)一次分类按一个标准;(3)分
讨论应逐级进行.
(3)转化化归思想:所谓化归思想就是化未知为已知、化繁为简、化难为易.如将分式
方程化为整式方程,将代数问题化为几何问题,将四边形问题转化为三角形问题等.实现
这种转化的方法有:待定系数法、配方法、整体代人法以及化动为静、由抽象到具体等.
(4)方程与函数思想:方程与函数是研究数量关系的重要工具,在处理某些问题时,往
往根据已知与未知之间的内在联系和相等关系建立方程(或方程组)或函数关系,这种通
过方程(组)或函数来沟通已知与未知,从而使问题获得解决的思想方法称之为方程与函
数思想.
二、典型例题
例1.(2009丽水)甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1) 他们在进行 ▲ 米的长跑训练,在0<x<15的时
段内,速度较快的人是 ▲ ;
(2) 求甲距终点的路程y(米)和跑步时间 x(分)之间的函数关系式;
(3) 当x=15时,两人相距多少米?在15<x<20的时段内,求两人速度之差.
例2.我市英山县某茶厂种植 “春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价y(元)与上市时间t(天)的关系可以近似地用如图1-3-6中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z(元)与上市时间t(天)的关系可以近似地用如图1-3-7的抛物线表示.
图1-3-6 图1-3-7
(1)直接写出图1-3-6中表示的市场销售单价y(元)与上市时间t(天)(t>0)的函数关系式;
(2)求出图1-3-7中表示的种植成本单价z(元)与上市时间t(天)(t>0)的函数关系式;
(3)认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大
(说明:市场销售单价和种植成本单价的单位:元/500克)
例3.在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得ΔAOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,……,Pk,(有k个就标到PK为止,不必写出画法) 求出坐标.
、
例4.(2006浙江湖州)如图,已知平面直角坐标系,A、B两点的坐标分别为A(2,-3),B(4,-1).
(1)若P(p,0)是x轴上的一个动点,则当p=____时,△PAB的周长最短;
(2)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=____时,四边形ABDC的周长最短;
(3)设M,N分别为x轴和y轴上的动点,请问:是否存在这样的点M(m,0)、N(0,n),使四边形ABMN的周长最短?若存在,请求出m=____,n=___(不必写解答过程);若不存在,请说明理由.
例5.(2009丽水)绿谷商场“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示:
类别 冰箱 彩电
进价(元/台) 2 320 1 900
售价(元/台) 2 420 1 980
(1) 按国家政策,农民购买“家电下乡”产品可享受售价13%的政府补贴.农民田大伯到该商场购买了冰箱、彩电各一台,可以享受多少元的政府补贴?
(2)为满足农民需求,商场决定用不超过85 000元采购冰箱、彩电共40台, 且冰箱的数量不少于彩电数量的.
①请你帮助该商场设计相应的进货方案;
②哪种进货方案商场获得利润最大(利润=售价进价),最大利润是多少?
例6.(2006湖南常德中考)把两块全等的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1-3-12(1),当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时AP·CQ=_________________.
(2)将三角板DEF由图1-3-12(1)所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP·CQ的值是否改变 说明你的理由.
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图1-3-12中(2)(3)供解题用).
数学思想方法同步练习
【基础巩固】
1.不等式组的解集在数轴上,如图表示应是 ( )
2.若等腰三角形的一个内角为50则其他两个内角为 ( )
A.500 ,80o B.650, 650
C.500 ,650 D.500,800或 650,650
3.一次函数y=kx+b的图象经过点A(0,-2)和B(-3,6)两点,那么该函数的表达式是 ( )
4.设一个三角形的三边长为3,l-2m,8,则m的取值范围是 ( )
A.0<m< B. -5<m- 2 C.-2<m <5 D.-<m<-l
5.如果表示a、b为两个实数的点在数轴上的位置如图3-l-8所示,那么化简的结果等于 ( )
A.2a B.2b C.-2a D.-2b
6.如图3-3-8所示,阴影部分是一个正方形,则此正方形的面积为 ( )
A.8 B.64 C.16 D.32
7.某村办工厂今年前5个月生产某种产品的总量 (件)关于时间t(月)的图象如图3-3-9所示,则该厂对这种产品来说 ( )
A.1月至3月每月生产总量逐月增加,4、5两月生产总量逐月减少;
B.1月至3月每月生产总量逐月增加,4、5两月生产总量与3月持平;
C.1月至3月每月生产总量逐月增加,4、5两月均停止生产;
D.1月至 3月每月生产总量不变,4、5两月均停止生产.
8.若
A.5或-1 B.-5或1; C.5或1 D.-5或-1
9.若解方程产生增根,则m的值是( )
A.-1或-2 B.-1或2 C.1或2 D.1或-2
10.水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如图甲所示,出水口出水量与时间的关系如图乙所示.某天0点到6点,该水池的蓄水量与时间的关系如图丙所示.
下列论断:①0点到1点,打开两个进水口,关闭出水口;②1点到3点,同时关闭两个进水口和-个出水口;③3点到4点,关门两个进水口,打开出水口;④5点到6点.同时打开两个进水口和一个出水口.其中,可能正确的论断是 ( )
A. ①③ B. ①④ C. ②③ D.②④
11.若一次函数的图象经过第一、二、四象限时,m的取值范围是_______.
12.已知直线y1=2x-1和y2=-x-1的图象如图3-3-24所示,根据图象填空.
⑴ 当x______时,y1>y2;当x______时,y1=y2;当x______时,y1<y2.
⑵ 方程组的解是_____________.
13. 已知二次函数与一次函数 y2=kx+ m(k≠0)的图象相交于点 A(-2,4),B(8,2)(如图 3-3-25所示),则能使y1>y2成立的x的取值范围是________.
14.已知直角三角形的两条边长分别和,则斜边上的高为 (结果保留根号).
15.将自然数按以下规律排列,则2008所在的位置是第 行第 列.
16.如图 3-1-2,梯形 ABCD中,AD∥BC,AB=CD,对角线AC、BD相交于O点,且AC⊥BD,AD=3,BC=5,求AC的长.
17.某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,图3-3-1已表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:
(1)求y1与y2的函数解析式;
(2)解释图中表示的两种方案是如何付推销费的?
(3)果你是推销员,应如何选择付费方案?
18.如图3-1-1,反比例函数y=-与一次函数y=-x+2的图象交于A、B两点.
(1)求 A、B两点的坐标;
(2)求△AOB的面积.
【能力拓展】
19.如图,已知直角坐标系内的梯形AOBC(O为原点),AC∥OB,OC⊥BC,AC,OB的长是关于x的方程x2-(k+2)x+5=0的两个根,且S△AOC:S△BOC=1:5.
(1)填空:0C=________,k=________;
(2)求经过O,C,B三点的抛物线的另一个交点为D,动点P,Q分别从O,D同时出发,都以每秒1个单位的速度运动,其中点P沿OB由O→B运动,点Q沿DC由D→C运动,过点Q作QM⊥CD交BC于点M,连结PM,设动点运动时间为t秒,请你探索:当t为何值时,△PMB是直角三角形.
第19题图
20.在四边形ABCD中,对角线AC平分∠DAB.如图(1),当∠DAB=120°,∠B=∠D=90°时,易证:AB+AD=AC.
(1) 如图(2),当∠DAB=120°,∠B与∠D互补时,线段AB、AD、AC有怎样的数量关系?写出你的猜想,并给予证明;
(2) 如图(3),当∠DAB=90°,∠B与∠D互补时,线段AB、AD、AC又有怎样的数量关系?写出你的猜想,不需证明.
第20题图
例题与同步练习参考答案
第九讲 数学思想方法(典型例题)
例1.解:(1)5000 甲
(2)设所求直线的解析式为:
y =kx+b(0≤x≤20),
由图象可知:b=5000,当x=20时,y=0,
∴0=20k+5000,解得k= -250.
即y = -250x+5000 (0≤x≤20)
(3)当x=15时,y = -250x+5000= -250×15+5000=5000-3750=1250.
两人相距:(5000 -1250)-(5000-2000)=750(米).
两人速度之差:750÷(20-15)=150(米/分)
例2.解:(1)依题意,可建立的函数关系式为
y=
(2)由题目已知条件可设z=a(t-110)2+20.
∵图象过点(60,),
∴=a(60-110)2+20.∴a=.
∴z=(t-110)2+20(t>0).
(3)设纯收益单价为W元,则W=销售单价-成本单价.
故W=
化简得W=
①当W=- (t-10)2+100(0
③当W=-(t-170)2+56(150≤t≤180)时,有t=170时,W最大,最大值为56.
综上所述,在t=10时,纯收益单价有最大值,最大值为100元.
例3.解:以A为圆心,OA为半径作圆交坐标轴得和;以O为圆心,OA为半径作圆交坐标轴得 ,,和;作OA的垂直平分线交坐标轴得和
例4.解:(1) (2)
(3)存在使四边形ABMN周长最短的点M.N,m=,n= HYPERLINK "http://" EMBED Equation.DSMT4 .
例5.解:(1) (2 420+1 980)×13%=572
答: 可以享受政府572元的补贴.
(2) ①设冰箱采购x台,则彩电采购(40-x)台,根据题意,得
2 320x+1 900(40-x)≤85 000,
x≥(40-x).
解不等式组,得≤x≤
∵x为正整数.
∴x= 19,20,21.
∴该商场共有3种进货方案:
方案一:冰箱购买19台,彩电购买21台
方案二:冰箱购买20台,彩电购买20台;
方案三:冰箱购买21台,彩电购买19台.
②设商场获得总利润y元,根据题意,得
y=(2 420 2 320)x+(1 980 40-x)=20x+3 200
∵20>0, ∴y随x的增大而增大
∴当x=21时,y最大=20×21+3 200=3 620
答:方案三商场获得利润最大,最大利润是3 620元
例6.解:(1)8
(2)AP·CQ的值不会改变,
理由如下: 如右图,在△APD与△CDQ中,∠A=∠C=45°,
∠APD=180°-45°-(45°+α)=90°-α,
∠CDQ=90°-α,即∠APD=∠CDQ.
∴△APD∽△CDQ.∴.
∴AP·CQ=AD·CD=AD2=(AC)2=8.
(3)如图,情形一:当0°<α<45°时,2
于是y=AB·AC-CQ·DN-AP·DG=8-x-(2
∴.
解得BM=.
∴MQ=4-BM-CQ=4-x-.
于是y=MQ·DN=4-x-(0
【基础巩固】
1—10 ADDBD; BCCDD 11.略12.略13.略14. 15.18 45
16. 解:过 D作DE⊥AC交BC的延长线于E,则得AD=CE.AC=DE.所以BE=BC+CE=8.
因为 AC⊥BD,所以BD⊥DE.
因为 AB=CD, 所以AC=BD.所以GD=DE.
在Rt△BDE中,BD2+DE2=BE2
所以BD=BE=4,即AC=4.
17.解:(1)y1=20x,y2=10x+300.
(2)y1是不推销产品没有推销费,每推销10件产品得推销费200元,y2是保底工资300元,每推销 10件产品再提成100元.
(3)若业务能力强,平均每月保证推销多于30件时,就选择y1的付费方案;否则,选择y2的付费方案.
18..解:⑴解方程组 得
所以A.B两点的坐标分别为A(-2,4)B(4,-2
(2)因为直线y=-x+2与y轴交点D坐标是(0, 2),
所以 所以
【能力拓展】
19.(1);(2)略
20. (1)AB+AD=AC证明如下:过C点分别作AD.AB的垂线,垂足分别为E.F。
∵ AC平分∠DAB,∴ CE=CF.∵ ∠D+∠ABC=180°,∠CBF+∠ABC=180°,
∴ ∠D=∠CBF.∵ ∠CED=∠CFB,∴ △CED≌△CFB .∴ ED=BF.∴ AD+AB=AE+ED+AB=AE+AF=AC . (2)AB+AD=AC.
(例1图)
例3图
A
B
C
D
图1
A
B
C
D
图(2)
A
B
C
D
图(3)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
