4.2 确定圆的条件

课件14张PPT。4. 确定圆的条件(1)
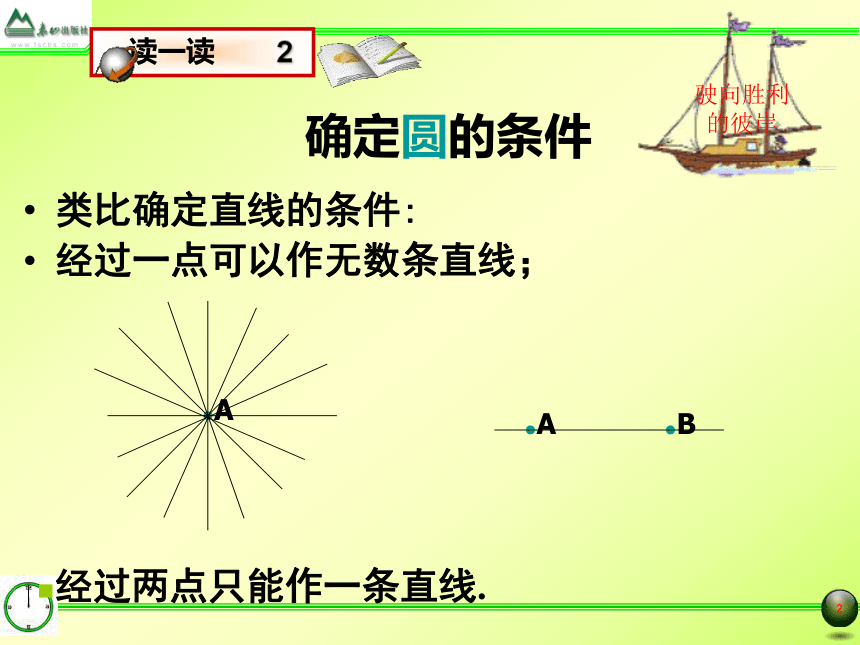
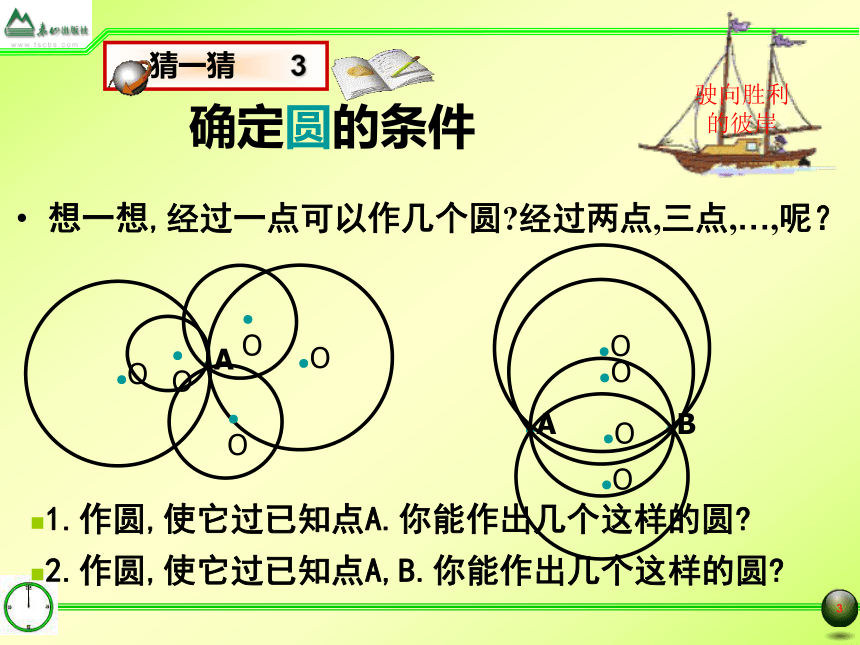
三点定圆九年级数学(上)第四章： 对圆的进一步认识确定圆的条件 类比确定直线的条件: 经过一点可以作无数条直线； 驶向胜利的彼岸经过两点只能作一条直线.●A●A●B驶向胜利的彼岸确定圆的条件想一想,经过一点可以作几个圆?经过两点,三点,…,呢？1.作圆,使它过已知点A.你能作出几个这样的圆?●A2.作圆,使它过已知点A,B.你能作出几个这样的圆?●A●B确定圆的条件2. 过已知点A,B作圆,可以作无数个圆.驶向胜利的彼岸经过两点A,B的圆的圆心在线段AB的垂直平分线上.
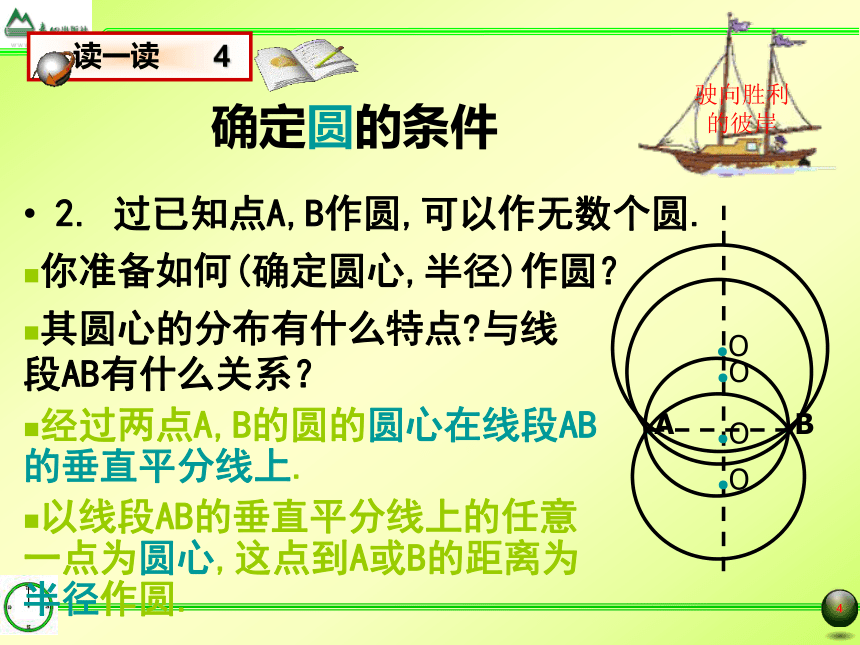
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.你准备如何(确定圆心,半径)作圆？其圆心的分布有什么特点?与线段AB有什么关系？●A●B确定圆的条件3.作圆,使它过已知点A,B,C(A,B,C三点不在同一条直线上),你能作出几个这样的圆?驶向胜利的彼岸老师提示:
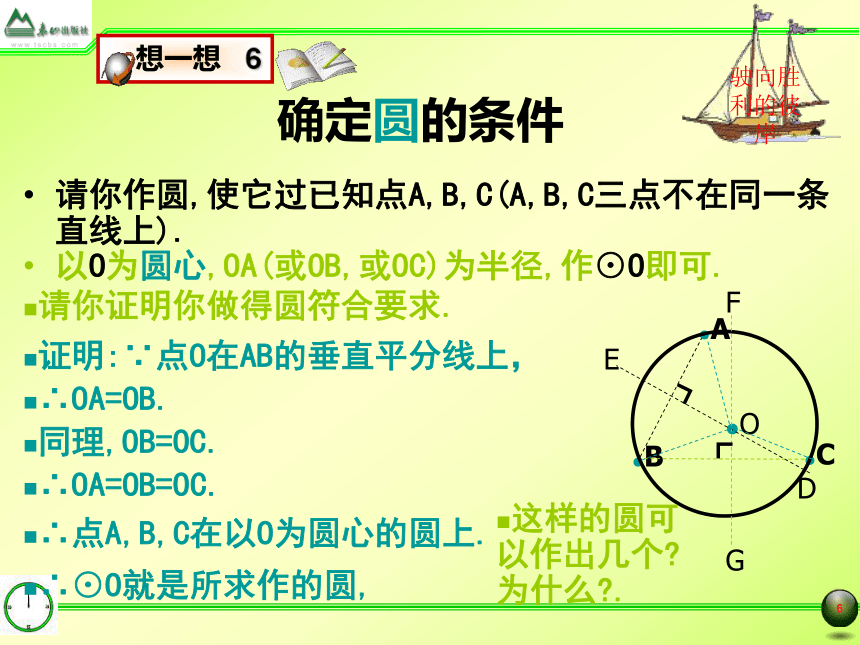
能否转化为2的情况:经过两点A,B的圆的圆心在线段AB的垂直平分线上. 你准备如何(确定圆心,半径)作圆？其圆心的位置有什么特点?与A,B,C有什么关系？●B●C经过两点B,C的圆的圆心在线段AB的垂直平分线上.●A经过三点A,B,C的圆的圆心应该这两条垂直平分线的交点O的位置.●O确定圆的条件请你作圆,使它过已知点A,B,C(A,B,C三点不在同一条直线上).以O为圆心,OA(或OB,或OC)为半径,作⊙O即可.驶向胜利的彼岸请你证明你做得圆符合要求.●B●C●A●O证明:∵点O在AB的垂直平分线上，∴⊙O就是所求作的圆,∴OA=OB.同理,OB=OC.∴OA=OB=OC.∴点A,B,C在以O为圆心的圆上.这样的圆可以作出几个?为什么?.三点定圆定理 不在一条直线上的三个点确定一个圆.在上面的作图过程中.驶向胜利的彼岸老师期望:
将这个结论及其证明作为一种模型对待.∵直线DE和FG只有一个交点O,并且点O到A,B,C三个点的距离相等,∴经过点A,B,C三点可以作一个圆,并且只能作一个圆.三角形与圆的位置关系因此,三角形的三个顶点确定一个圆,这圆叫做三角形的外接圆.这个三角形叫做圆的内接三角形.外接圆的圆心是三角形三边垂直平分线的的交点,叫做三角形的外心.老师提示:
多边形的顶点与圆的位置关系称为接.四边形与圆的位置关系如果四边形的四个顶点在一个圆,这圆叫做四边形的外接圆.这个四边形叫做圆的内接四边形.我们可以证明圆内接四边的两个重要性质:
1.圆内接四边形对角互补.
2.圆内接四边形对的一个外角等于它的内对角.
3.对角互补的四边形内接于圆.D如图：圆内接四边形ABCD中， ∵ ∠BAD等于弧BCD所对圆心角的一半,∠BCD等于弧BAD所对圆心角的一半.
而弧BCD所对的圆心角+弧BAD所对的圆心角=360°， ∴∠BAD＋∠BCD＝180°. 同理∠ABC＋∠ADC＝180°.圆内接四边形的对角互补.四边形与圆的位置关系如果延长BC到E，那么
∠DCE＋∠BCD ＝180°.∴∠A＝∠DCE.又 ∵∠A ＋∠BCD＝ 180°，四边形与圆的位置关系因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角.圆内接四边形的一个外角等于它的内对角.三角形与圆的位置关系分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.老师期望:
作三角形的外接圆是必备基本技能,定要熟练掌握.挑战自我 习题4.2 1-3题祝你成功!驶向胜利的彼岸结束寄语盛年不重来,一日难再晨,及时宜自勉,岁月不待人.再见