4.3 圆周角和圆心角的关系(1)圆周角定理.
文档属性
| 名称 | 4.3 圆周角和圆心角的关系(1)圆周角定理. |  | |
| 格式 | rar | ||
| 文件大小 | 535.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-29 19:55:00 | ||
图片预览



文档简介
课件12张PPT。3. 圆周角和圆心角的关系
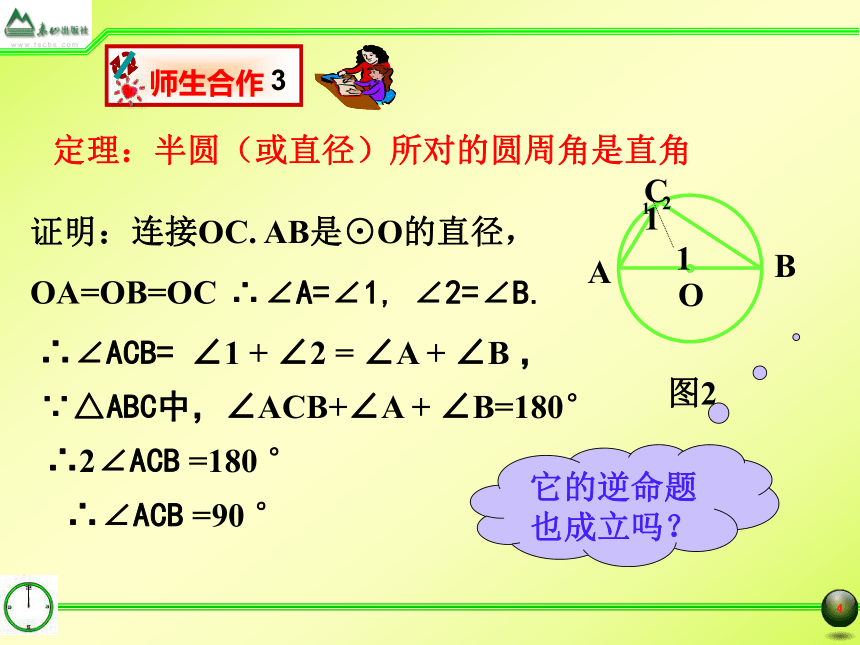
(1)圆周角定理九年级数学(上)第四章: 对圆的进一步认识圆周角在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.圆周角也可以看作两条有公共端点的弦所夹的角.问题1、如图2,AB是⊙O的直径,C是⊙O上任一点,那么你发现了些什么结论?定理:半圆(或直径)所对的圆周角是直角1112证明:连接OC. AB是⊙O的直径,
OA=OB=OC ∴∠A=∠1,∠2=∠B.∴∠ACB= ∠1 + ∠2 = ∠A + ∠B ,∵△ABC中,∠ACB+∠A + ∠B=180° ∴2∠ACB =180 ° ∴∠ACB =90 ° 它的逆命题
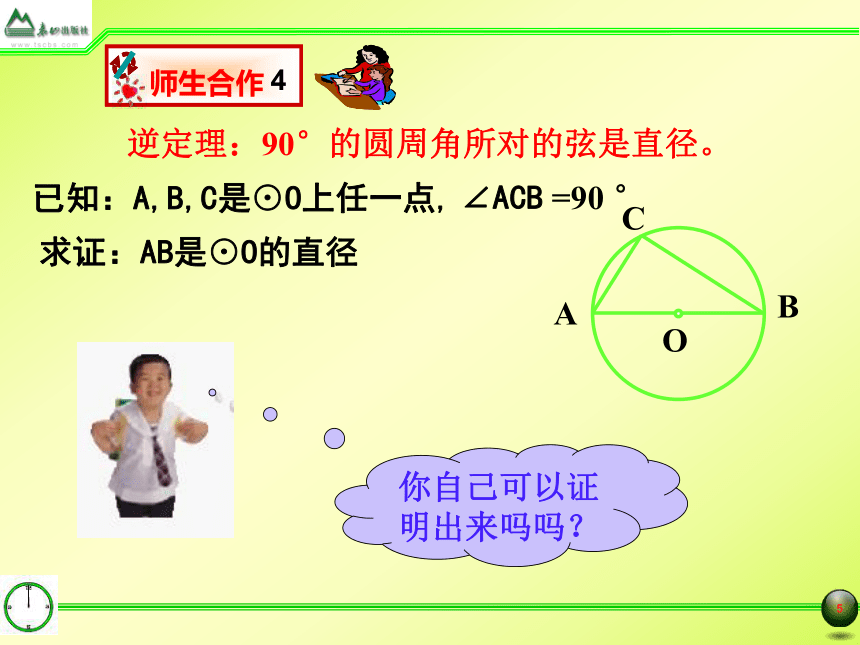
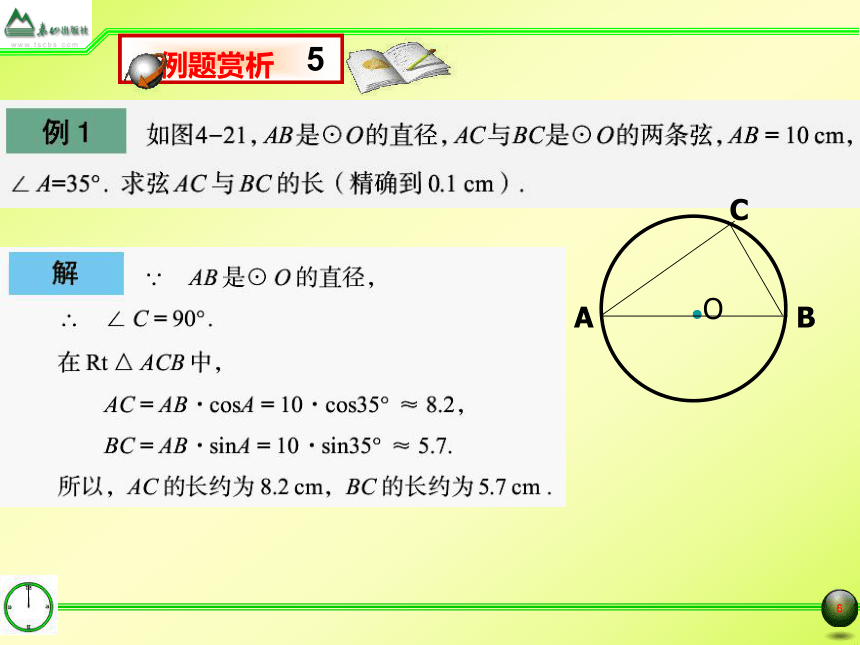
也成立吗?逆定理:90°的圆周角所对的弦是直径。已知:A,B,C是⊙O上任一点,求证:AB是⊙O的直径∠ACB =90 ° 你自己可以证明出来吗吗?如图, AB是⊙O的直径,C是⊙O上任一点,CD⊥AB,垂足为D,图中有哪些成比例线段?△ACD∽ △CBD ∽ △ABCD补充例题例2、如图,AD是△ABC的高,AE是△ABC的外接圆直径。求证:AB · AC = AE · ADAOBCDE分析:要证AB · AC = AE · AD△ADC∽ △ABE或△ACE∽ △ADB题后思:1、证明题的思路寻找方法;
2、等积式的证明方法;
3、辅助线的思考方法。如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE小结与作业1、本节课我们学习了哪些知识?
2、证明等积式的一般思路你掌握了吗? 课后作业(完成时间:25分钟):
练习题T3 习题4.3:T1,T2结束寄语盛年不重来,一日难再晨,及时宜自勉,岁月不待人.再见
(1)圆周角定理九年级数学(上)第四章: 对圆的进一步认识圆周角在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.圆周角也可以看作两条有公共端点的弦所夹的角.问题1、如图2,AB是⊙O的直径,C是⊙O上任一点,那么你发现了些什么结论?定理:半圆(或直径)所对的圆周角是直角1112证明:连接OC. AB是⊙O的直径,
OA=OB=OC ∴∠A=∠1,∠2=∠B.∴∠ACB= ∠1 + ∠2 = ∠A + ∠B ,∵△ABC中,∠ACB+∠A + ∠B=180° ∴2∠ACB =180 ° ∴∠ACB =90 ° 它的逆命题
也成立吗?逆定理:90°的圆周角所对的弦是直径。已知:A,B,C是⊙O上任一点,求证:AB是⊙O的直径∠ACB =90 ° 你自己可以证明出来吗吗?如图, AB是⊙O的直径,C是⊙O上任一点,CD⊥AB,垂足为D,图中有哪些成比例线段?△ACD∽ △CBD ∽ △ABCD补充例题例2、如图,AD是△ABC的高,AE是△ABC的外接圆直径。求证:AB · AC = AE · ADAOBCDE分析:要证AB · AC = AE · AD△ADC∽ △ABE或△ACE∽ △ADB题后思:1、证明题的思路寻找方法;
2、等积式的证明方法;
3、辅助线的思考方法。如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE小结与作业1、本节课我们学习了哪些知识?
2、证明等积式的一般思路你掌握了吗? 课后作业(完成时间:25分钟):
练习题T3 习题4.3:T1,T2结束寄语盛年不重来,一日难再晨,及时宜自勉,岁月不待人.再见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
