4.4 直线和圆的位置关系(2)切线判定及性质定理.
文档属性
| 名称 | 4.4 直线和圆的位置关系(2)切线判定及性质定理. |  | |
| 格式 | rar | ||
| 文件大小 | 628.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-08-29 19:55:00 | ||
图片预览


文档简介
课件14张PPT。5.直线和圆的位置关系(2)
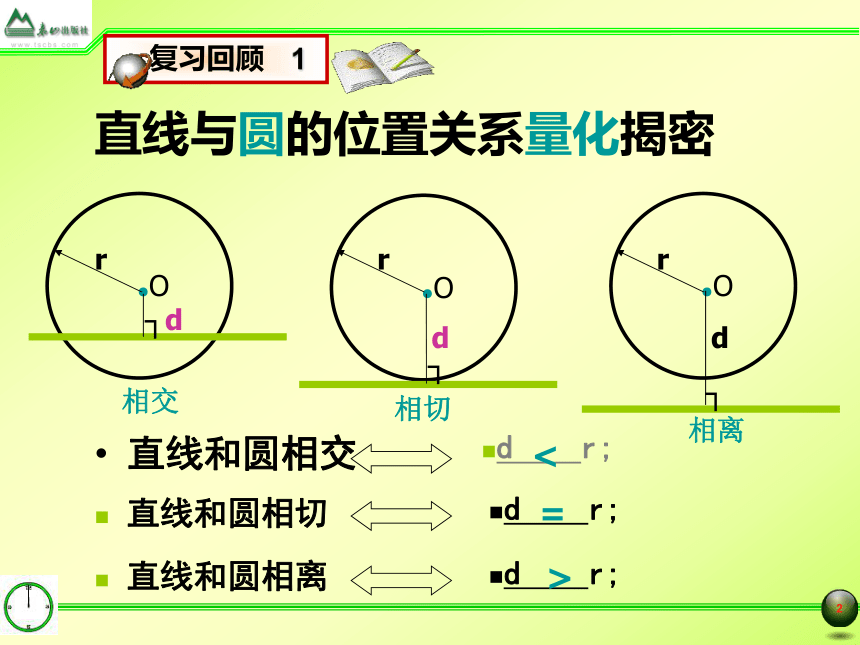
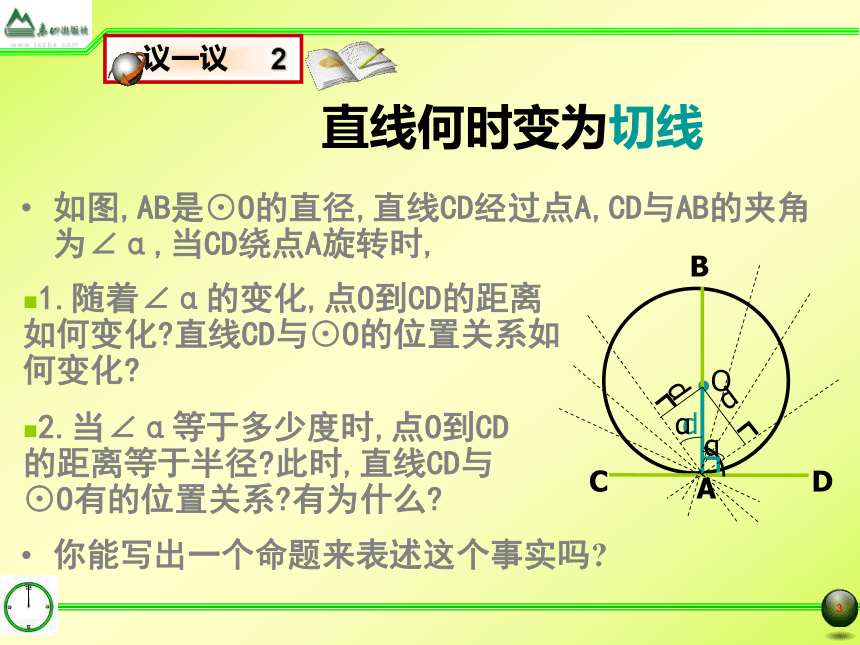
切线及切线性质定理九年级数学(上)第四章: 对圆的进一步认识直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系量化揭密<=>直线何时变为切线如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,你能写出一个命题来表述这个事实吗?1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有的位置关系?有为什么?切线的判定定理定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.老师提示:
切线的判定定理是证明一条直线是否是圆的切线的根据;作过切点的半径是常用经验辅助线之一.如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
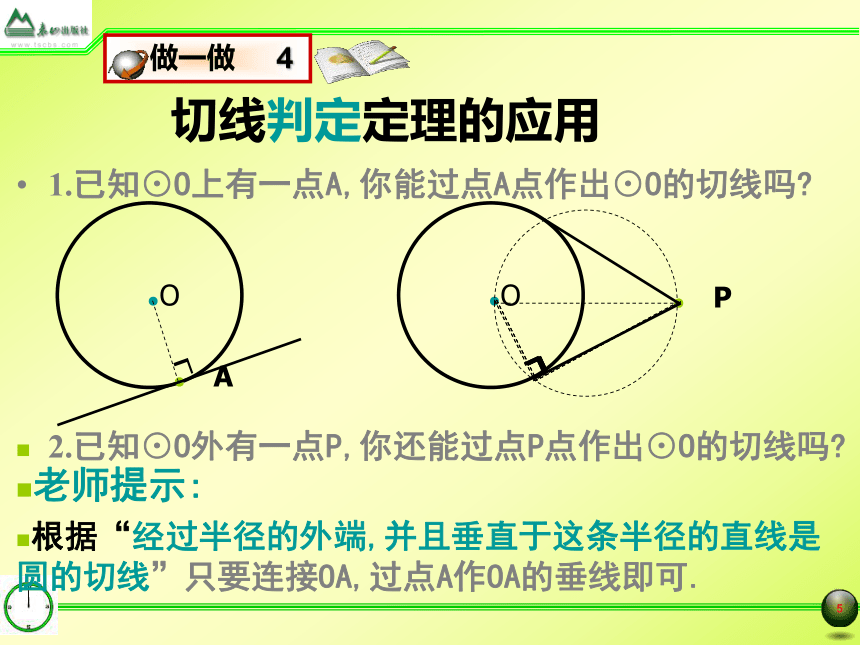
∴ CD是⊙O的切线.切线判定定理的应用1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?老师提示:
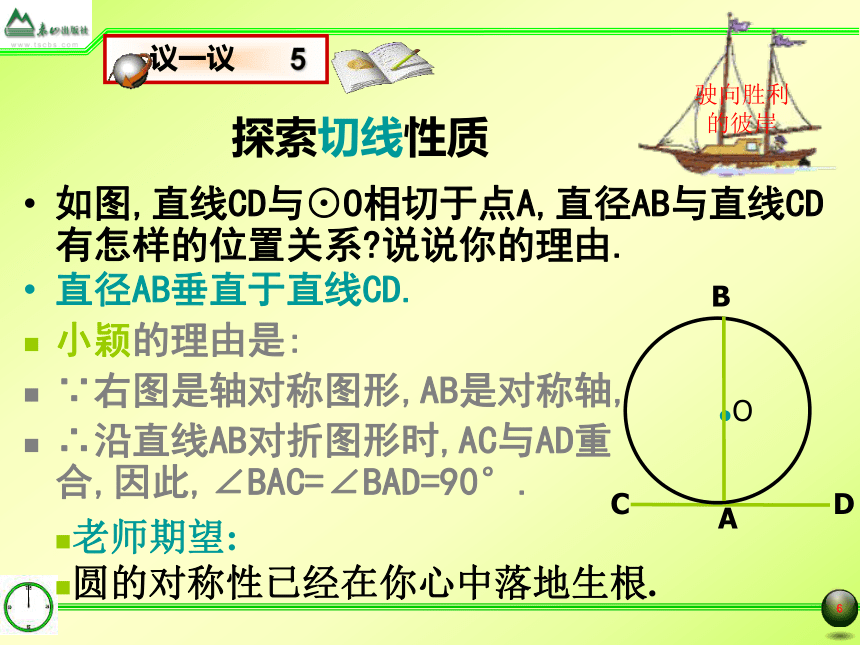
根据“经过半径的外端,并且垂直于这条半径的直线是圆的切线”只要连接OA,过点A作OA的垂线即可.2.已知⊙O外有一点P,你还能过点P点作出⊙O的切线吗?探索切线性质如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.直径AB垂直于直线CD.老师期望:
圆的对称性已经在你心中落地生根.小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
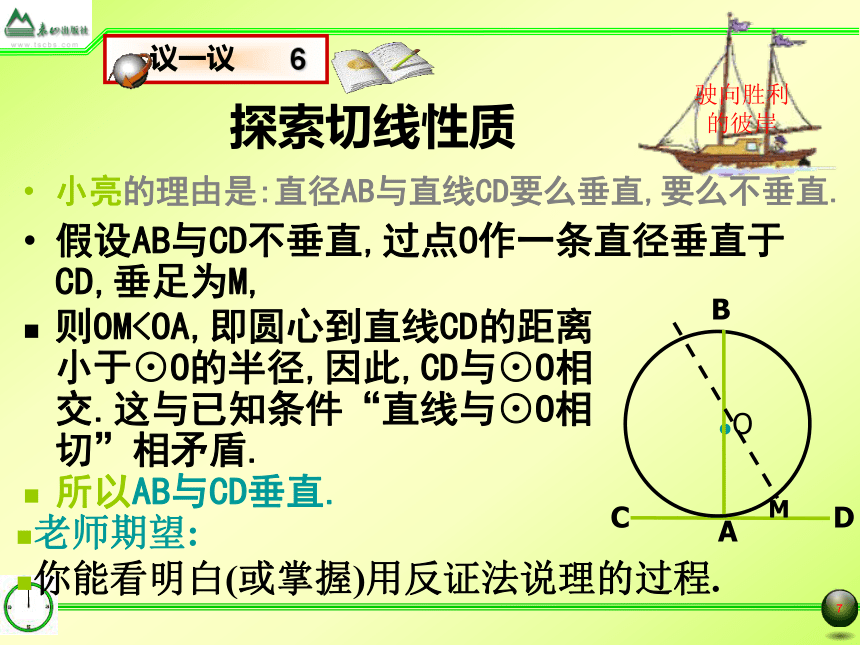
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.探索切线性质小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,老师期望:
你能看明白(或掌握)用反证法说理的过程.则OM切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.如图
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,∴CD⊥OA.切线的性质定理的应用切线的性质定理的应用1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围..2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少?.老师提示:硬币滚动一圈,圆心经过的路经是与直线平行的一条线段,其长度等于圆的周长.挑战自我1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切线,A,B是切点.请你观察猜想,PA,PB有怎样的关系?并证明你的结论.2.由1所得的结论及证明过程,你还能发现那些新的结论?如果有,仍请你予以证明.老师提示:根据这个结论写出的命题称为切线长定理及其推论.挑战自我 习题4.4 3-5题祝你成功!结束寄语具有丰富知识和经验的人,比只须一种知识和经验更容易产生新的联想和独到的见解。再见
切线及切线性质定理九年级数学(上)第四章: 对圆的进一步认识直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系量化揭密<=>直线何时变为切线如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,你能写出一个命题来表述这个事实吗?1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有的位置关系?有为什么?切线的判定定理定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.老师提示:
切线的判定定理是证明一条直线是否是圆的切线的根据;作过切点的半径是常用经验辅助线之一.如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.切线判定定理的应用1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?老师提示:
根据“经过半径的外端,并且垂直于这条半径的直线是圆的切线”只要连接OA,过点A作OA的垂线即可.2.已知⊙O外有一点P,你还能过点P点作出⊙O的切线吗?探索切线性质如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.直径AB垂直于直线CD.老师期望:
圆的对称性已经在你心中落地生根.小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.探索切线性质小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,老师期望:
你能看明白(或掌握)用反证法说理的过程.则OM
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,∴CD⊥OA.切线的性质定理的应用切线的性质定理的应用1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围..2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少?.老师提示:硬币滚动一圈,圆心经过的路经是与直线平行的一条线段,其长度等于圆的周长.挑战自我1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切线,A,B是切点.请你观察猜想,PA,PB有怎样的关系?并证明你的结论.2.由1所得的结论及证明过程,你还能发现那些新的结论?如果有,仍请你予以证明.老师提示:根据这个结论写出的命题称为切线长定理及其推论.挑战自我 习题4.4 3-5题祝你成功!结束寄语具有丰富知识和经验的人,比只须一种知识和经验更容易产生新的联想和独到的见解。再见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
