《圆》整章测试
图片预览

文档简介
《圆》整章测试
一、选择题
1. ⊙O的半径为R,点P到圆心O的距离为d,并且d≥R,则P点 ( )
A.在⊙O内或圆周上 B.在⊙O外
C.在圆周上 D.在⊙O外或圆周上
2. ⊙O的半径为5,直线a上有一点到圆心O的距离等于5,则直线a与⊙O的位置关系是( )
A. 相离 B. 相切 C. 相切或相交 D. 相交
3.三角形内切圆的圆心是( )
A.三内角平分线的交点 B.边中垂线的交点
C.中线的交点 D.高线的交点
4.已知两圆的半径之和为12 cm,半径之差为4 cm,圆心距为4 cm,则两圆的位置关系( )
A.外离 B.外切 C.相交 D.内切
5.如图,是⊙0的两条切线,切点是.如果 ,那么等于 ( )
A. B. C. D.
6.如图,半径分别为1,2,3的三个圆两两相外切,则此三个圆的圆心的连线构成的三角形的面积等于( )
A.6 B.7 C.8 D.9
7.⊙O的半径为6,⊙O的一条弦AB长6,以3为半径⊙O的同心圆与直线AB的位置关系是( ) A.相离 B.相交 C.相切 D.不能确定
8.如图,PA切⊙O于A,AB⊥OP于B,若PO=8 cm, BO=2 cm,则PA的长为( )
A.16 cm B.48 cm C.6 cm D.4 cm
二、填空题
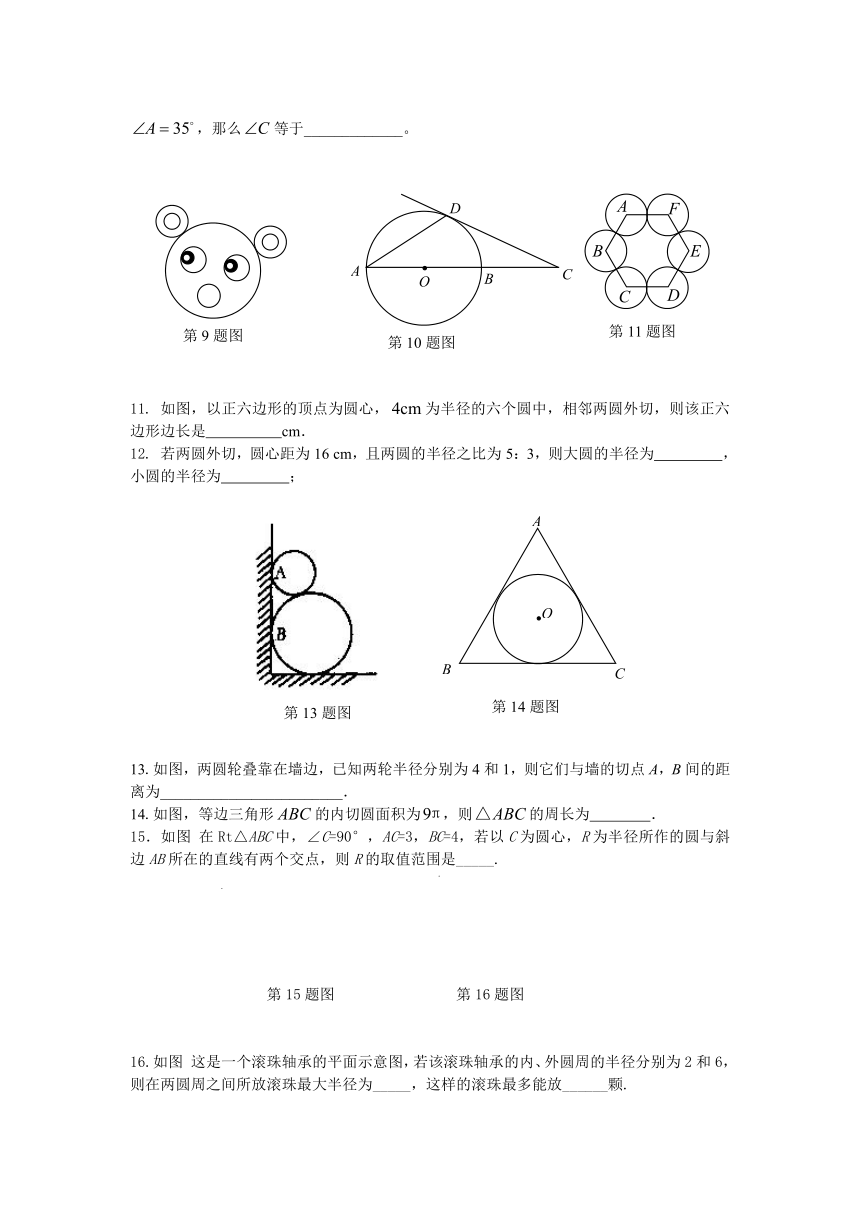
9. 两圆有多种位置关系,图中不存在的位置关系是 .
10. 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切,切点为D.如果,那么等于_____________。
11. 如图,以正六边形的顶点为圆心,为半径的六个圆中,相邻两圆外切,则该正六边形边长是 cm.
12. 若两圆外切,圆心距为16 cm,且两圆的半径之比为5:3,则大圆的半径为 ,
小圆的半径为 ;
13.如图,两圆轮叠靠在墙边,已知两轮半径分别为4和1,则它们与墙的切点A,B间的距离为________________________.
14.如图,等边三角形的内切圆面积为,则的周长为 .
15.如图 在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径所作的圆与斜边AB所在的直线有两个交点,则R的取值范围是_____.
第15题图 第16题图
16.如图 这是一个滚珠轴承的平面示意图,若该滚珠轴承的内、外圆周的半径分别为2和6,则在两圆周之间所放滚珠最大半径为_____,这样的滚珠最多能放______颗.
三、解答题
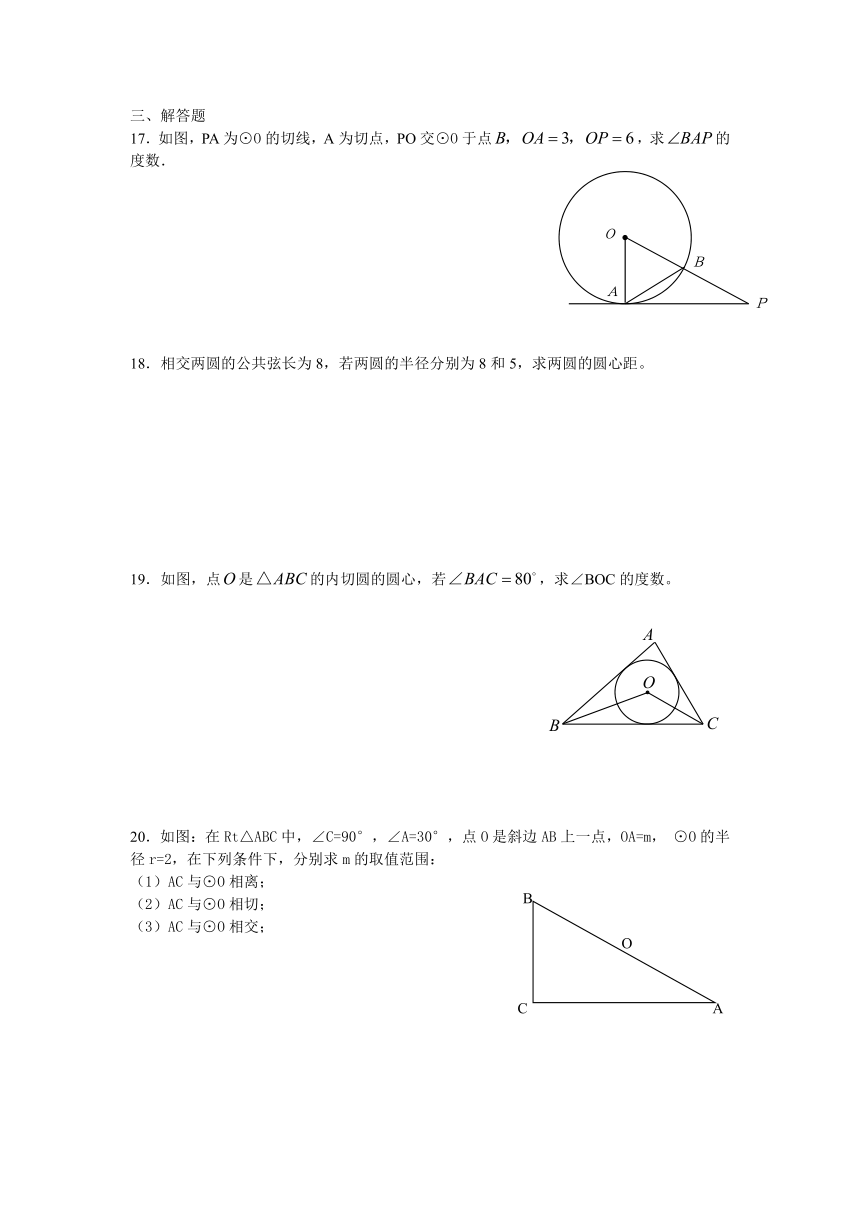
17.如图,PA为⊙O的切线,A为切点,PO交⊙O于点,求的度数.
18.相交两圆的公共弦长为8,若两圆的半径分别为8和5,求两圆的圆心距。
19.如图,点是的内切圆的圆心,若,求∠BOC的度数。
20.如图:在Rt△ABC中,∠C=90°,∠A=30°,点O是斜边AB上一点,OA=m, ⊙O的半径r=2,在下列条件下,分别求m的取值范围:
(1)AC与⊙O相离;
(2)AC与⊙O相切;
(3)AC与⊙O相交;
21.已知:,为边上一点,以为圆心,2为半径作,交于两点,设,
(1)如图(1),当为何值时,⊙O与相切?
(2)如图(2),当为何值时,⊙O与相交于两点且?
四、附加题
22.如图22-1、22-2、22-3、22-n分别是⊙O的内接正三角形正方形、正五边形、、正边形的边上的点,且,连结.
(1) 求图9-1中的度数;
(2) 图9-2中的度数是 ,图9-3中的度数是 ;
(3) 试探究的度数与正边形边数的关系(直接写出答案).
答案:
一、选择题 D C A D D A C D
二、填空题 9. 相交 10. 20度 11. 8 12. 10cm,6cm
13. 4 14. 15.2.4<R≤3 16. 2, 6
三、解答题
17.解:为的切线,为切点
.
在中
.
在中 .
.
18.解:如图AC=4,AO1=8 ∴CO1=
AC=4,AO2=5 ∴CO2=3
∴O1 O2=+3
19.解:∵
∴∠ABC+∠ACB=1000
∵点是的内切圆的圆心
即点O是角平分线的交点
∴∠OBC+∠OCB=500
∴∠BOC=1300
20.解:过点O作OD⊥AC于
∵OA=m, ∠C=90°,∠A=30°
∴OD=0.5m
(1)若AC与⊙O相离, 则有OD>r
即0.5m>2
∴m>4
(2)若AC与⊙O相切, 则有OD=r
即0.5m=2
∴m=4
(3)若AC与⊙O相交, 则有OD<r
即0.5m<2
∴m<4
答:当m>4,AC与⊙O相离;当m=4,AC与⊙O相切;当m<4,AC与⊙O相交。
21.解:(1)过点作于,
当时,⊙O与相切.
此时,故.
(2)过点作于.
,,.
,,
,
,,.
22.解:(1)法一:连结.
正内接于,,
又
.
法二:连结.
正内接于,
.
又
.
.
(2).
(3)
B
P
A
O
A
O
B
C
D
C
B
A
O
N
F
G
A
B
C
D
E
O
B
A
O
P
M
A
B
C
C
D
A
B
O
O
A
B
C
D
E
M
N
N
M
O
图22-1
图22-2
图22-3
图22-n
N
M
C
B
图(2)
M
N
E
D
O
A
图(1)
M
N
E
D
O
A
第9题图
第8题图
第6题图
第5题图
O
B
C
A
O
B
C
A
第10题图
第11题图
第13题图
第14题图
C
B
A
O2
O1
一、选择题
1. ⊙O的半径为R,点P到圆心O的距离为d,并且d≥R,则P点 ( )
A.在⊙O内或圆周上 B.在⊙O外
C.在圆周上 D.在⊙O外或圆周上
2. ⊙O的半径为5,直线a上有一点到圆心O的距离等于5,则直线a与⊙O的位置关系是( )
A. 相离 B. 相切 C. 相切或相交 D. 相交
3.三角形内切圆的圆心是( )
A.三内角平分线的交点 B.边中垂线的交点
C.中线的交点 D.高线的交点
4.已知两圆的半径之和为12 cm,半径之差为4 cm,圆心距为4 cm,则两圆的位置关系( )
A.外离 B.外切 C.相交 D.内切
5.如图,是⊙0的两条切线,切点是.如果 ,那么等于 ( )
A. B. C. D.
6.如图,半径分别为1,2,3的三个圆两两相外切,则此三个圆的圆心的连线构成的三角形的面积等于( )
A.6 B.7 C.8 D.9
7.⊙O的半径为6,⊙O的一条弦AB长6,以3为半径⊙O的同心圆与直线AB的位置关系是( ) A.相离 B.相交 C.相切 D.不能确定
8.如图,PA切⊙O于A,AB⊥OP于B,若PO=8 cm, BO=2 cm,则PA的长为( )
A.16 cm B.48 cm C.6 cm D.4 cm
二、填空题
9. 两圆有多种位置关系,图中不存在的位置关系是 .
10. 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切,切点为D.如果,那么等于_____________。
11. 如图,以正六边形的顶点为圆心,为半径的六个圆中,相邻两圆外切,则该正六边形边长是 cm.
12. 若两圆外切,圆心距为16 cm,且两圆的半径之比为5:3,则大圆的半径为 ,
小圆的半径为 ;
13.如图,两圆轮叠靠在墙边,已知两轮半径分别为4和1,则它们与墙的切点A,B间的距离为________________________.
14.如图,等边三角形的内切圆面积为,则的周长为 .
15.如图 在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径所作的圆与斜边AB所在的直线有两个交点,则R的取值范围是_____.
第15题图 第16题图
16.如图 这是一个滚珠轴承的平面示意图,若该滚珠轴承的内、外圆周的半径分别为2和6,则在两圆周之间所放滚珠最大半径为_____,这样的滚珠最多能放______颗.
三、解答题
17.如图,PA为⊙O的切线,A为切点,PO交⊙O于点,求的度数.
18.相交两圆的公共弦长为8,若两圆的半径分别为8和5,求两圆的圆心距。
19.如图,点是的内切圆的圆心,若,求∠BOC的度数。
20.如图:在Rt△ABC中,∠C=90°,∠A=30°,点O是斜边AB上一点,OA=m, ⊙O的半径r=2,在下列条件下,分别求m的取值范围:
(1)AC与⊙O相离;
(2)AC与⊙O相切;
(3)AC与⊙O相交;
21.已知:,为边上一点,以为圆心,2为半径作,交于两点,设,
(1)如图(1),当为何值时,⊙O与相切?
(2)如图(2),当为何值时,⊙O与相交于两点且?
四、附加题
22.如图22-1、22-2、22-3、22-n分别是⊙O的内接正三角形正方形、正五边形、、正边形的边上的点,且,连结.
(1) 求图9-1中的度数;
(2) 图9-2中的度数是 ,图9-3中的度数是 ;
(3) 试探究的度数与正边形边数的关系(直接写出答案).
答案:
一、选择题 D C A D D A C D
二、填空题 9. 相交 10. 20度 11. 8 12. 10cm,6cm
13. 4 14. 15.2.4<R≤3 16. 2, 6
三、解答题
17.解:为的切线,为切点
.
在中
.
在中 .
.
18.解:如图AC=4,AO1=8 ∴CO1=
AC=4,AO2=5 ∴CO2=3
∴O1 O2=+3
19.解:∵
∴∠ABC+∠ACB=1000
∵点是的内切圆的圆心
即点O是角平分线的交点
∴∠OBC+∠OCB=500
∴∠BOC=1300
20.解:过点O作OD⊥AC于
∵OA=m, ∠C=90°,∠A=30°
∴OD=0.5m
(1)若AC与⊙O相离, 则有OD>r
即0.5m>2
∴m>4
(2)若AC与⊙O相切, 则有OD=r
即0.5m=2
∴m=4
(3)若AC与⊙O相交, 则有OD<r
即0.5m<2
∴m<4
答:当m>4,AC与⊙O相离;当m=4,AC与⊙O相切;当m<4,AC与⊙O相交。
21.解:(1)过点作于,
当时,⊙O与相切.
此时,故.
(2)过点作于.
,,.
,,
,
,,.
22.解:(1)法一:连结.
正内接于,,
又
.
法二:连结.
正内接于,
.
又
.
.
(2).
(3)
B
P
A
O
A
O
B
C
D
C
B
A
O
N
F
G
A
B
C
D
E
O
B
A
O
P
M
A
B
C
C
D
A
B
O
O
A
B
C
D
E
M
N
N
M
O
图22-1
图22-2
图22-3
图22-n
N
M
C
B
图(2)
M
N
E
D
O
A
图(1)
M
N
E
D
O
A
第9题图
第8题图
第6题图
第5题图
O
B
C
A
O
B
C
A
第10题图
第11题图
第13题图
第14题图
C
B
A
O2
O1
