平行四边形及复习
图片预览

文档简介
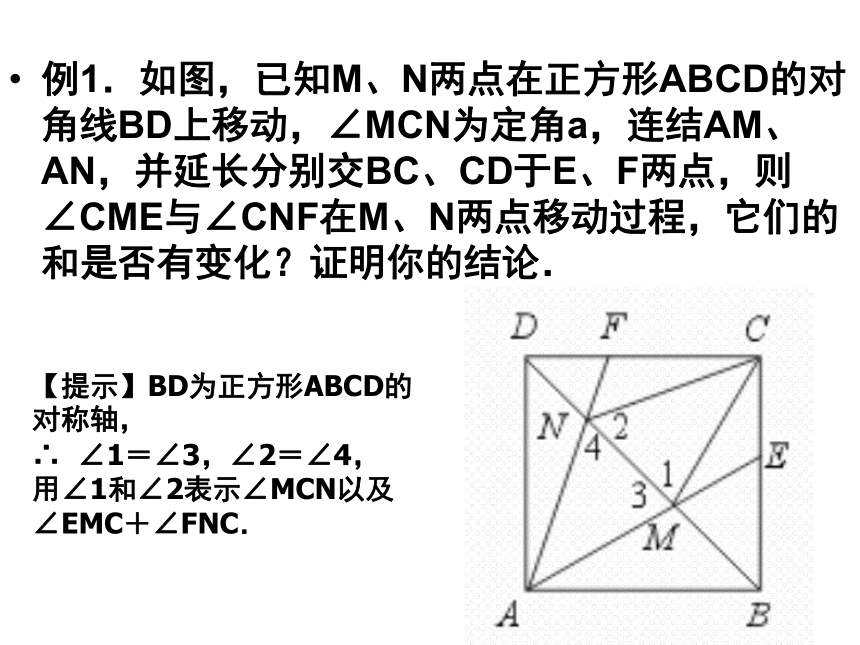
课件12张PPT。平行四边形及特殊平行四边形复习2上海民办明珠中学 周雷例1.如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角a,连结AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.【提示】BD为正方形ABCD的对称轴,
∴ ∠1=∠3,∠2=∠4,
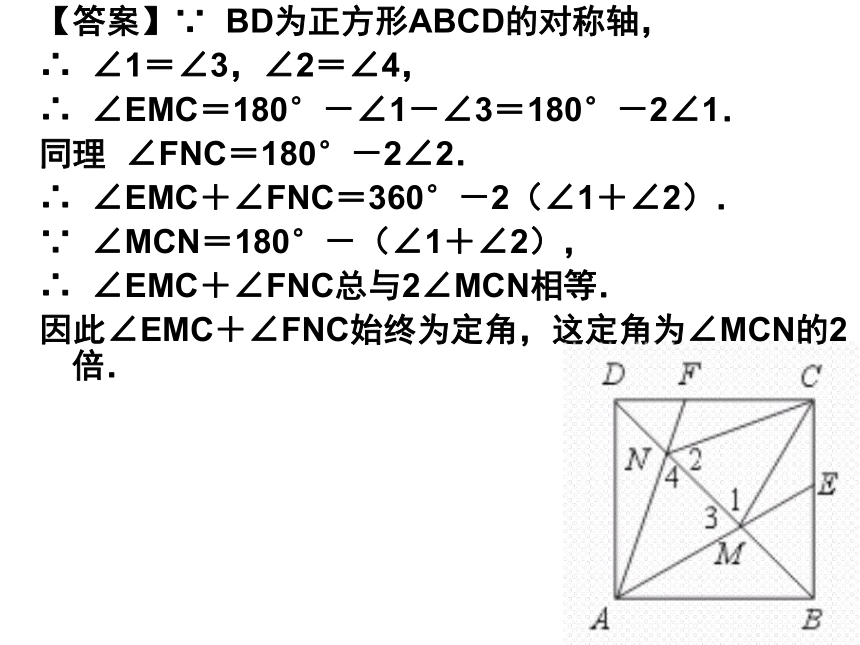
用∠1和∠2表示∠MCN以及∠EMC+∠FNC.【答案】∵ BD为正方形ABCD的对称轴,
∴ ∠1=∠3,∠2=∠4,
∴ ∠EMC=180°-∠1-∠3=180°-2∠1.
同理 ∠FNC=180°-2∠2.
∴ ∠EMC+∠FNC=360°-2(∠1+∠2).
∵ ∠MCN=180°-(∠1+∠2),
∴ ∠EMC+∠FNC总与2∠MCN相等.
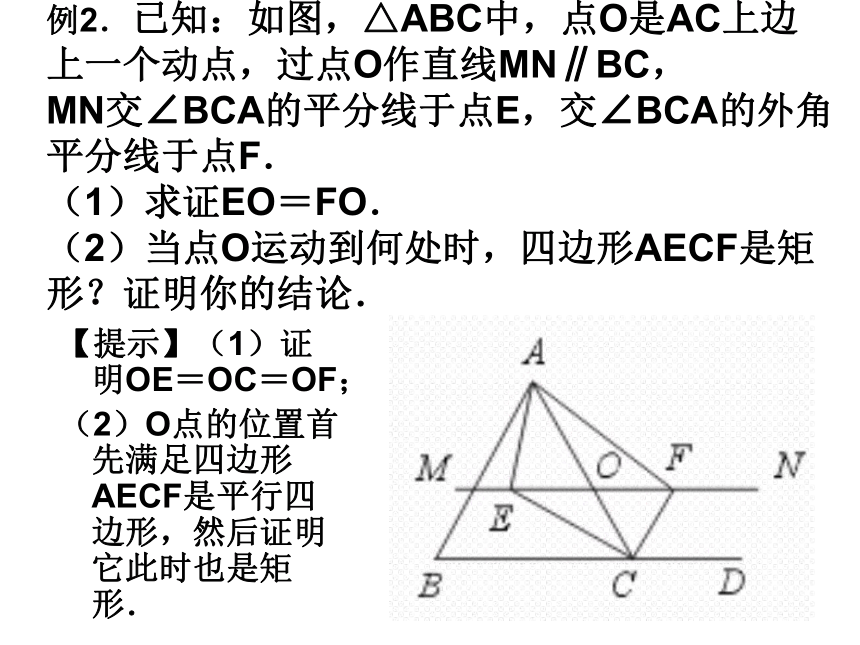
因此∠EMC+∠FNC始终为定角,这定角为∠MCN的2倍.例2.已知:如图,△ABC中,点O是AC上边上一个动点,过点O作直线MN∥BC, MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. (1)求证EO=FO. (2)当点O运动到何处时,四边形AECF是矩形?证明你的结论.【提示】(1)证明OE=OC=OF;
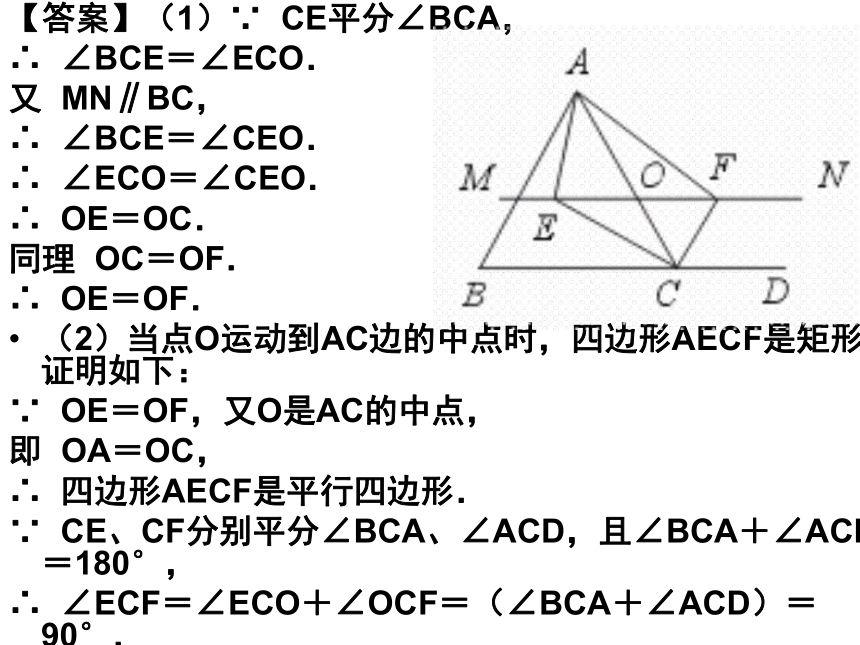
(2)O点的位置首先满足四边形AECF是平行四边形,然后证明它此时也是矩形.【答案】(1)∵ CE平分∠BCA,
∴ ∠BCE=∠ECO.
又 MN∥BC,
∴ ∠BCE=∠CEO.
∴ ∠ECO=∠CEO.
∴ OE=OC.
同理 OC=OF.
∴ OE=OF.
(2)当点O运动到AC边的中点时,四边形AECF是矩形,证明如下:
∵ OE=OF,又O是AC的中点,
即 OA=OC,
∴ 四边形AECF是平行四边形.
∵ CE、CF分别平分∠BCA、∠ACD,且∠BCA+∠ACD=180°,
∴ ∠ECF=∠ECO+∠OCF=(∠BCA+∠ACD)=90°.
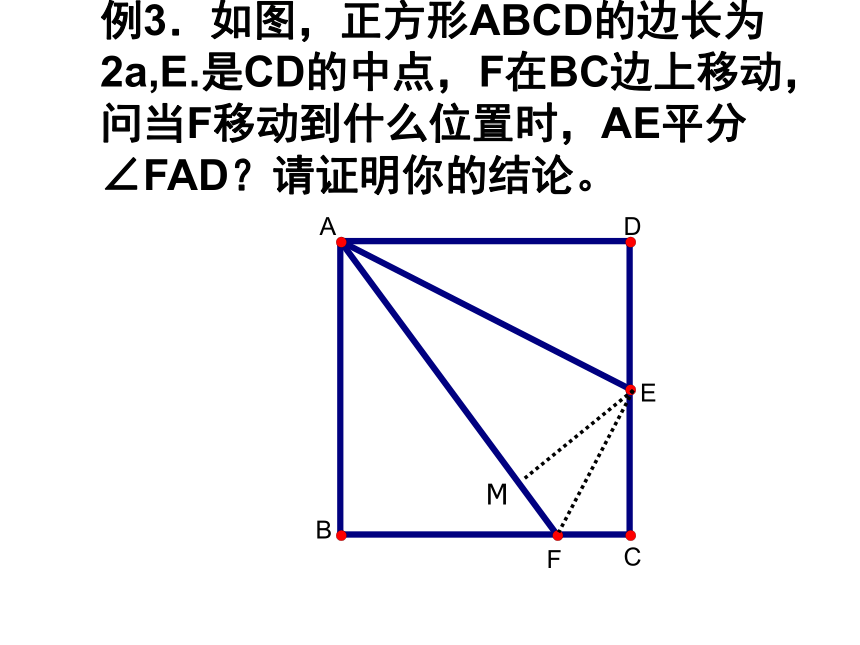
∴ □AECF是矩形.例3.如图,正方形ABCD的边长为2a,E.是CD的中点,F在BC边上移动,问当F移动到什么位置时,AE平分∠FAD?请证明你的结论。 例4 如图,已知点E、F分别在正方形ABCD的边BC、CD上,且AE平分∠FAD
求证:BF+DE=AF例5:如图,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由 一、 选择题.
1. 下列条件中能判定一个四边形是平行四边形的是( )
A. 一组对边相等 B. 一组对边平行
C. 两条对角线相等 D. 两组对角分别相等
2. 如图所示,直线AF∥BG,AB∥CD,CE⊥BG,
FG ⊥ BG,E、G为垂足,则下列说法错误的是( )
A. AB=CD B. EC=FG
C. 点C和直线BG的距离就是线段CE的长
D. 直线AF与直线BG的距离就是线段CD的长
DD加油哇!!看谁做得快!! D3.正方形具备而矩形不具备的特征是 ( )
A. 四个角都是直角 B.对角线互相平分
C. 对角线相等 D.对角线互相垂直
4. 若菱形的两条对角线的长分别为4cm和6cm,则它
的面积为( )
A. 3cm2 B. 6cm2 C. 12cm2 D. 24cm2
5.如图所示,在平行四边形ABCD中,DB=DC,
∠C=70°,AE⊥BD于E,则∠DAE等于( )
A. 20° B. 25° C. 30° D. 35°
6.在平行四边形ABCD中,AC⊥AB,且∠ABC:∠BCA=2:1,则∠ABC与∠BCD之比为( )
A. 1:1 B. 1:2 C. 1:3 D. 1:4
CAB努力呀!!加油哇!!C7. 如图所示,平行四边形ABCD的对角线相交于O点,且AB≠BC,过O点作OE⊥AC,交BC于E,如果△ABE的周长为b,则平行四边形ABCD的周长是( )
A. b B. 1.5b C. 2b D. 3b
练习:三、 解答题.
菱形ABCD中,对角线AC,BD交于点O,E、F分别是AB、AD中点,是说明OE=OF.
如图E为正方形ABCD外一点, △CDE为等边三角形,求∠AED的度数.
∴ ∠1=∠3,∠2=∠4,
用∠1和∠2表示∠MCN以及∠EMC+∠FNC.【答案】∵ BD为正方形ABCD的对称轴,
∴ ∠1=∠3,∠2=∠4,
∴ ∠EMC=180°-∠1-∠3=180°-2∠1.
同理 ∠FNC=180°-2∠2.
∴ ∠EMC+∠FNC=360°-2(∠1+∠2).
∵ ∠MCN=180°-(∠1+∠2),
∴ ∠EMC+∠FNC总与2∠MCN相等.
因此∠EMC+∠FNC始终为定角,这定角为∠MCN的2倍.例2.已知:如图,△ABC中,点O是AC上边上一个动点,过点O作直线MN∥BC, MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. (1)求证EO=FO. (2)当点O运动到何处时,四边形AECF是矩形?证明你的结论.【提示】(1)证明OE=OC=OF;
(2)O点的位置首先满足四边形AECF是平行四边形,然后证明它此时也是矩形.【答案】(1)∵ CE平分∠BCA,
∴ ∠BCE=∠ECO.
又 MN∥BC,
∴ ∠BCE=∠CEO.
∴ ∠ECO=∠CEO.
∴ OE=OC.
同理 OC=OF.
∴ OE=OF.
(2)当点O运动到AC边的中点时,四边形AECF是矩形,证明如下:
∵ OE=OF,又O是AC的中点,
即 OA=OC,
∴ 四边形AECF是平行四边形.
∵ CE、CF分别平分∠BCA、∠ACD,且∠BCA+∠ACD=180°,
∴ ∠ECF=∠ECO+∠OCF=(∠BCA+∠ACD)=90°.
∴ □AECF是矩形.例3.如图,正方形ABCD的边长为2a,E.是CD的中点,F在BC边上移动,问当F移动到什么位置时,AE平分∠FAD?请证明你的结论。 例4 如图,已知点E、F分别在正方形ABCD的边BC、CD上,且AE平分∠FAD
求证:BF+DE=AF例5:如图,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由 一、 选择题.
1. 下列条件中能判定一个四边形是平行四边形的是( )
A. 一组对边相等 B. 一组对边平行
C. 两条对角线相等 D. 两组对角分别相等
2. 如图所示,直线AF∥BG,AB∥CD,CE⊥BG,
FG ⊥ BG,E、G为垂足,则下列说法错误的是( )
A. AB=CD B. EC=FG
C. 点C和直线BG的距离就是线段CE的长
D. 直线AF与直线BG的距离就是线段CD的长
DD加油哇!!看谁做得快!! D3.正方形具备而矩形不具备的特征是 ( )
A. 四个角都是直角 B.对角线互相平分
C. 对角线相等 D.对角线互相垂直
4. 若菱形的两条对角线的长分别为4cm和6cm,则它
的面积为( )
A. 3cm2 B. 6cm2 C. 12cm2 D. 24cm2
5.如图所示,在平行四边形ABCD中,DB=DC,
∠C=70°,AE⊥BD于E,则∠DAE等于( )
A. 20° B. 25° C. 30° D. 35°
6.在平行四边形ABCD中,AC⊥AB,且∠ABC:∠BCA=2:1,则∠ABC与∠BCD之比为( )
A. 1:1 B. 1:2 C. 1:3 D. 1:4
CAB努力呀!!加油哇!!C7. 如图所示,平行四边形ABCD的对角线相交于O点,且AB≠BC,过O点作OE⊥AC,交BC于E,如果△ABE的周长为b,则平行四边形ABCD的周长是( )
A. b B. 1.5b C. 2b D. 3b
练习:三、 解答题.
菱形ABCD中,对角线AC,BD交于点O,E、F分别是AB、AD中点,是说明OE=OF.
如图E为正方形ABCD外一点, △CDE为等边三角形,求∠AED的度数.
